2025 July 28;6(7):962-975. doi: 10.37871/jbres2151.
Degrees of Freedom and Conserved Quantities in Golfer-Environment Systems: An Ecological Analysis of Visual Kinesthesis and Screw Dynamics in the Golf Swing
Wangdo Kim*
- Visual kinesthesis
- Ecological perception
- Screw theory
- Pitch invariance
- Perceptual-motor integration
- Haptic feedback
- Degrees of freedom
- Conserved quantities
- Affordance-action coupling
- Golf biomechanics
Abstract
We propose a new ecological theory of golf swing coordination based on the interaction between degrees of freedom and conserved quantities in golfer–environment systems. Using screw theory and motion capture data, we analyze pitch invariance along the Instantaneous Screw Axis (ISA) as a conserved action structure. Crucially, we introduce visual kinesthesis-the perception of displacement through optic flow-as a key perceptual anchor during impact, when proprioceptive cues are unreliable.
Our findings show that skilled golfers exploit stable ISA trajectories and tightly coupled pitch–force dynamics to produce perceptually invariant motion. Visual kinesthesis, not feedback correction, guides this coordination, while haptic kines- thesis governs internal calibration during the swing. These results suggest that pitch and ISA geometry function as conserved quantities, providing an ecological foundation for understanding skill as emergent sensorimotor alignment.
Introduction
Skilled human movement often conveys a paradoxical sense of stillness in the midst of dynamic mechanical motion. Nowhere is this more apparent than in the golf swing-a complex, whole-body action that blends translational and rotational dynamics into a fluid, highly coordinated performance. Understanding how such motion is structured not merely at the level of joints or muscles, but across the body-environment system, requires a theoretical framework that captures both the geometry of motion and the perceptual basis of control.
A conventional approach to modeling movement dynamics employs the rigid body approximation [1], wherein linked anatomical segments are assumed to move cohesively, preserving spatial relationships during motion [2,3]. Despite biological softness and flexibility, this abstraction proves useful, especially in high-speed ballistic actions like a golf downswing, where inertial coupling dominates and segments behave as if rigidly linked. Within this model, the motion of any segment is described by its Instantaneous Screw Axis (ISA)-a spatial line that captures the combined rotational and translational components of movement [4].
Originally formalized by Ball (1900), screw theory [4,5] provides a powerful geometric language for representing motion through twists (velocity screws) and wrenches (force screws), bypassing the limitations of angle-based or joint-centric representations [6]. Of particular interest is the pitch of the screw-defined as the ratio of linear to angular velocity along the ISA-which functions as a compact descriptor of the balance between translation and rotation. When pitch remains stable across time, it indicates uniform screw motion, often associated with coordinated, efficient execution. Conversely, irregular pitch variation can signal asymmetry, compensatory action, or loss of biomechanical coherence.
Importantly, our approach diverges from traditional feedback control models, which assume that movement is governed by internal error correction and optimization. In those models, control signals (e.g., torques or forces) are adjusted in real time based on discrepancies between a desired and an actual state. However, this model is poorly suited to explain the perceptual experience and behavioral fluency of skilled performance, where control appears seamless, anticipatory, and not explicitly computed.
Instead, we adopt an ecological perspective grounded in visual kinesthesis [7]-Gib- son’s term for the integration of proprioceptive and visual information in real-time move- ment perception. From this view, movement is not guided by internal models or state estimates but by perceptual attunement to affordances [8]: the structural features of the environment that invite and constrain action. The environment-its surfaces, contours, and textures-acts not as a passive backdrop but as a co-participant in the control loop. Thus, control is not localized within the brain or body but is distributed across the actor-environment system.
In the context of the golf swing, the visual layout of the ball, tee, and ground surface sculpts the body’s posture and trajectory-not by supplying feedback, but by providing perceptual structure that invites particular forms of action. The ISA [9], while mechanically real, is not directly perceivable; it resides in the geometry of empty space. What is perceivable are the surfaces, alignments, and motions of body and tool in the environment. We argue that skilled golfers do not perceive or adjust the ISA directly, but instead align their movements with visual and haptic invariants that reflect and co-generate screw-like dynamics.
In this study, we reanalyze a previously validated motion capture dataset of two golfers [10]-a proficient and a novice-during the downswing phase. By computing the evolution of pitch along the ISA and synchronizing this with Ground Reaction Force (GRF) data, we assess how segmental coordination is shaped not through feedback but through perceptual-motor coupling. Our results demonstrate that a stable pitch profile tightly coupled with GRF patterns marks proficient performance, while irregular pitch and asynchrony signify loss of ecological attunement.
By situating screw theory within a perceptual framework [7], we propose a hybrid model: perceptual stillness emerges not from mechanical quiescence, but from attunement to invariants in the environment. This approach reconceptualizes motor coordination as the emergent resonance between mechanical structure and perceptual layout-an insight with broad implications for motor learning, rehabilitation, and performance optimization.
Material and Methods
Spatial inertia tensor and the Eigen-screw problem
The spatial inertia tensor [10] M ∈ R6×6 encapsulates both translational and rotational dynamics of a rigid body, and is defined as:
where m is the mass, rc is the vector from the body frame to the center of mass, Ic is the 3 × 3 rotational inertia tensor about the center of mass, and [·]× denotes the skew-symmetric matrix operator.
The eigenvalue problem seeks screw vectors ϑ = ω ∈ R6 that satisfy:
Here, ω is the angular velocity, and v is the linear velocity. When ω ̸= 0, the pitch h of the screw is defined as:
This pitch captures the ratio of translation along to rotation about the screw axis. In the case of a finite twist, the pitch can also be derived from geometric terms:
Here, L = [L, M, N]T defines the direction of the screw, and Π# is the raw moment vector. For the screw to remain well-defined in Pluckier coordinates [6], Π# must be proportional to L.
Harmonic screws and one-body oscillation
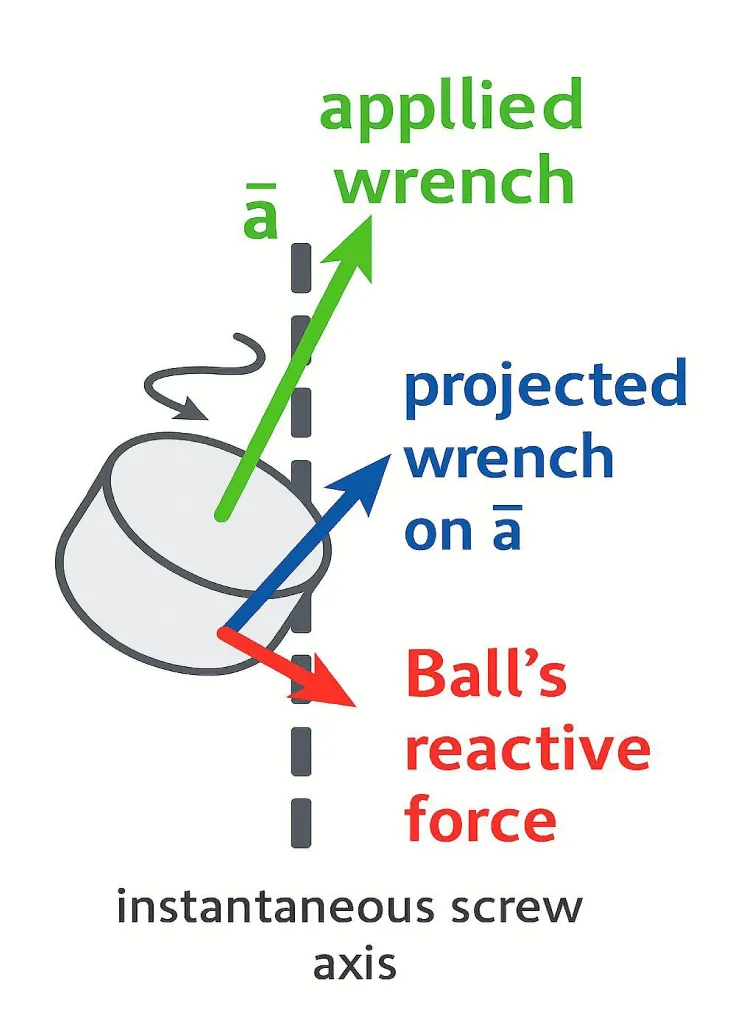
According to Ball’s screw theory [4], any wrench acting on a rigid body constrained to twist about a given screw a can be expressed as a projection onto that screw. The principle of reciprocity demands that for equilibrium to be maintained, the virtual work performed by the wrenches during a twist δϑ about a must vanish (Figures 1,2):
Here, Pi is the magnitude of the i-th wrench, and ϕi is the screw coordinate projection onto a. This equilibrium condition enables us to model rhythmic oscillatory motion-such as that found in skilled sports movement-as the interplay of reactive and applied forces along reciprocal screw systems.
These “harmonic screws” describe stable, self-consistent twist-wrench pairings. In the context of athletic performance, they reveal invariant biomechanical structures underlying dynamic balance and momentum regulation.
Ecological Modeling and Operationalization of Pitch and ISA
The club motion during the downswing phase is modeled using a discrete-time first-order dynamic system, where the evolution of the state variable [11] is governed by:
Here:
xj is the state variable at discrete time step j, representing a kinematic descriptor of the club (e.g., orientation, position, or pitch),
gj is the forcing term (input or adjustment) applied at time step j,
m is a constant scalar that defines the propagation or memory of the system from one frame to the next,
xj+1 is the predicted state at time step j+1.
Suppose we have a sequence of N measurements denoted by dj, where j = 1, . . . , N . These measurements could represent observed pitch values, marker positions, or other biomechanical signals derived from motion capture. The objective is to estimate the sequence of forcing terms {gj}N j=1 and the initial condition x1 that minimize the following cost function [12]:
where:
E is the total error or cost to be minimized,
dj is the measured or desired state at time step j,
xj is the predicted state based on the model,
gj is the control input or adjustment applied,
b is a regularization parameter that balances fidelity to data (first term) against smoothness or energy minimization in control (second term).
The first term penalizes deviations from the observed measurements, while the second term discourages excessive forcing. This formulation ensures that the solution is not overly sensitive to noise in dj and avoids over fitting [11].
By framing the estimation of club dynamics this way, we interpret the evolution of pitch and ISA not as perceptually tracked control variables, but as latent internal adjustments consistent with observed kinematic flow. The forcing terms gj are not derived from internal feedback per se, but can be understood as implicit adjustments embed- ded in the movement structure, shaped by affordances and co-participant environmental constraints.
Rather than modeling the swing as a closed-loop control system governed by feedback:
we adopt a feedforward, ecological perspective:
where a(t) is the action, E(t) is the structured environment (e.g., slope, surface), and π is the perceptual mapping. From this perspective, pitch and ISA trajectories are not simply derived state variables but serve as operationally defined observables that express the coordination of translation and rotation. Pitch-the ratio of translational to angular velocity along the ISA-is treated as a conserved quantity, a hallmark of biomechanical coherence. ISA trajectories, visualized as helicoidal paths, encode the coupling of joint torques and segmental rotations into a unified motion flow.
Together, pitch invariance and ISA regularity act as ecological constraints that re- duce the effective degrees of freedom, facilitating coordinated action. These variables are not perceptual inputs in themselves-ISA, for instance, is mechanically defined-but their spatiotemporal evolution shapes the optic flow and haptic cues available to the performer. Thus, they serve as the bridge between abstract theoretical constraints (degrees of freedom and conservation laws) and measurable outcomes (ground reaction force synchrony, optic flow coherence, and motor regularity), enabling an empirically grounded analysis of skilled movement.
Conserved quantities as action invariants in swing motion
This study was specifically designed to explore conserved quantities-such as pitch in- variance and screw axis geometry-during varying golf swing motions. Unlike traditional biomechanical approaches that emphasize isolated joint angles or error correction, our framework views the swing as a dynamic system governed by ecological constraints. Within this framework, the concept of a conservation-an invariant quantity that persists despite surface-level variation-provides a powerful lens for identifying stability within complex movement.
Conserved quantities are fundamental in dynamic systems theory. They describe properties that remain unchanged before and after transformation, serving as reliable indicators of system organization. In the context of the golf swing, pitch (the ratio of linear to angular velocity along the instantaneous screw axis) is hypothesized to act as such a conserved measure. When movement patterns change-either due to skill level, trial variability, or environmental conditions-pitch invariance, if present, marks a deeper stability beneath the variation.
To test this hypothesis, we computed Instantaneous Screw Axes (ISAs) and associated pitch profiles across the downswing phase. Our goal was to determine whether these measures remain stable within and across swing conditions. We posit that the presence of conserved pitch dynamics would indicate a lawful coordination structure-one that expert golfers are more capable of exploiting, and that novices tend to disrupt.
Conserved action measures offer a unique benefit: they allow the swing to be evaluated not merely as a kinematic event but as a structured transformation. This enables:
Direct comparison between novice and expert performance using invariant metrics.
Assessment of learning or adaptation over time by tracking convergence toward invariance.
Quantification of task difficulty by analyzing deviations from expected conservation.
By focusing on invariants such as pitch and ISA coherence, our experimental approach uncovers the deeper geometric and perceptual structure of skillful movement. These findings suggest that expert performance is not about precisely repeating a trajectory, but about preserving conserved relations amid variation-achieving functional stability through lawful constraint.
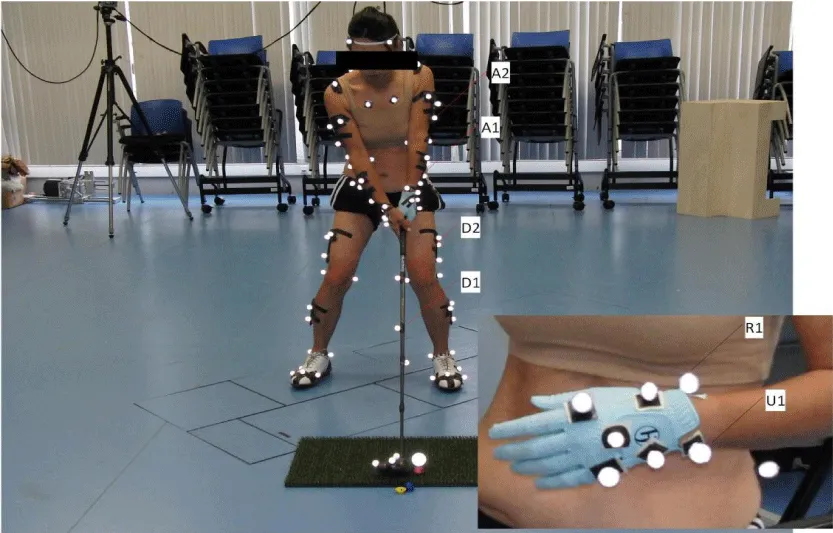
We analyzed a validated dataset of full-body golf swings performed by two female participants (a proficient and a novice), recorded using a 12-camera Qualisys motion capture system (300 Hz) and synchronized Ground Reaction Force (GRF) data from a Kistler force platform. Marker placement followed ISAK standards, with additional markers on the club shaft and grip (Figure 3). See table 1 for participant demographics.
| Table 1: Participant demographics and golfing background. | ||||||
| Participant | Age | Height | Mass | Handicap | Experience | Rounds/year |
| Proficient Golfer | 17 | 167 cm | 54 kg | 32 | 1 yr | 10 |
| Novice Golfer | 51 | 165 cm | 55 kg | 8 | 15 yrs | 110 |
The club segment was modeled as a rigid body using six reflective markers. For each frame, we computed relative transformations between marker positions at t and t + ∆t using singular value decomposition. Rotation matrices and translational displacements were used to reconstruct screw parameters. The instantaneous screw axis and pitch were computed at each timestep [13], and compared against GRF data to assess synchronization and coordination.
The pitch series was analyzed as an indicator of rotational-translational coupling quality, while ISA trajectories were visualized to assess motion regularity. Together, these serve as biomechanical correlates of perceptual-motor integration.
To empirically ground the theoretical constructs of constraints and affordances, we structured the experimental procedure around the analysis of measurable kinematic and kinetic data from golf swings. The goal was to map biomechanical observables-such as Instantaneous Screw Axis (ISA) trajectories, pitch stability, and Ground Reaction Force (GRF)-to the underlying ecological and dynamical principles that govern skilled movement.
Mechanical Constraints: We modeled physical constraints using the inertia tensor and ISA of the club-body system. The inertia tensor characterizes the resistance to angular acceleration and defines the system’s distribution of mass, thereby constraining its available Degrees of Freedom (DOF). The ISA, computed from motion capture data, represents the screw axis about which the system naturally rotates and translates. These structural features of the rigid body system serve as invariant constraints that limit how motion can be expressed.
Informational Constraints (Affordances): Concurrently, we treated visual information available during the swing-particularly during the impact phase-as ecological constraints. The optic flow resulting from the club’s motion relative to the environment was used to define affordances: actionable information about the environment’s layout that supports perceptual-motor coordination. During the approach to impact, the ball’s location, contour, and background visually specify opportunities for action that are dynamically tuned by the golfer.
Visual Kinesthesis: This affordance-guided motion relies on visual kinesthesis, a feed- forward perceptual process wherein the evolving optic array informs motor output in real time. Rather than functioning as a reactive feedback mechanism, visual kinesthesis provides anticipatory alignment between body and environment. The swing path is sculpted by the visibility of the ball and the perceived contour of the ground rather than by correcting errors in internal parameters.
Together, these operational definitions allowed us to analyze swing dynamics as the interaction between constrained mechanical DOF and perceptual guidance from environ- mental information. This framework supports a unified interpretation of motor coordination in the context of embodied ecological cognition.
Visual kinesthesis and the perception of pure translation at impact
During the critical moment of impact in a golf swing, skilled performers exhibit a remark- able ability to align the motion of the club head with a perceptually grounded invariant: a visually smooth, linear translation. This perceptual experience-what Gibson termed visual kinesthesis-refers to the direct awareness of one’s own motion, not through internal computation or proprioceptive feedback alone, but through the structure of the optic array and environmental interaction.
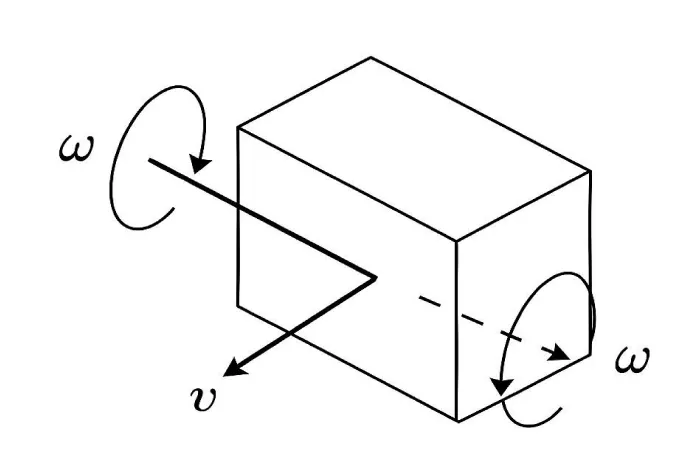
In biomechanical terms, the club head’s motion at impact can be approximated as a pure translation-a uniform linear velocity vector field v across the surface of the club. This uniform motion does not arise passively. Instead, it results from the golfer’s coordinated use of their body to cancel out rotational asymmetries and deliver a translational effect that is both mechanically efficient and perceptually stable.
To achieve this pure translational effect, the golfer’s body acts as a dynamic generator of angular momentum. Specifically, the lower body and upper body are activated as a couple-that is, two opposing angular velocities of equal magnitude but opposite direction are applied about distinct axes [14]. This biomechanical configuration mirrors the screw-theoretic case in which:
Here, ω is the resultant angular velocity vector (from the combined action of upper and lower body rotations), and d is the vector from the axis of rotation to a point on the club head. When the couple is balanced such that the rotational effects cancel at the club head, the resulting motion field v becomes spatially uniform-i.e., a pure translation.
This uniform field of linear velocities is perceivable as a steady, visually smooth path of the club head through space. Rather than detecting angular velocities or force signals, the performer aligns to the visual displacement of the club head, a feature readily observable in both peripheral vision and through tactile feedback from the grip. This alignment is a form of perceptual tuning: the body self-organizes not to control the ISA directly, but to make the motion of the club head look and feel like a translation.
Figure 4 provides a mechanical analogy [14]. When a rigid body is subjected to equal and opposite angular velocities, it exhibits a parallel field of linear velocities, effectively translating the entire body uniformly. Expert golfers, through years of practice, internal- ize and exploit this principle-using their body as a screw-coupled actuator to visually stabilize the motion of the club head at the moment of impact.
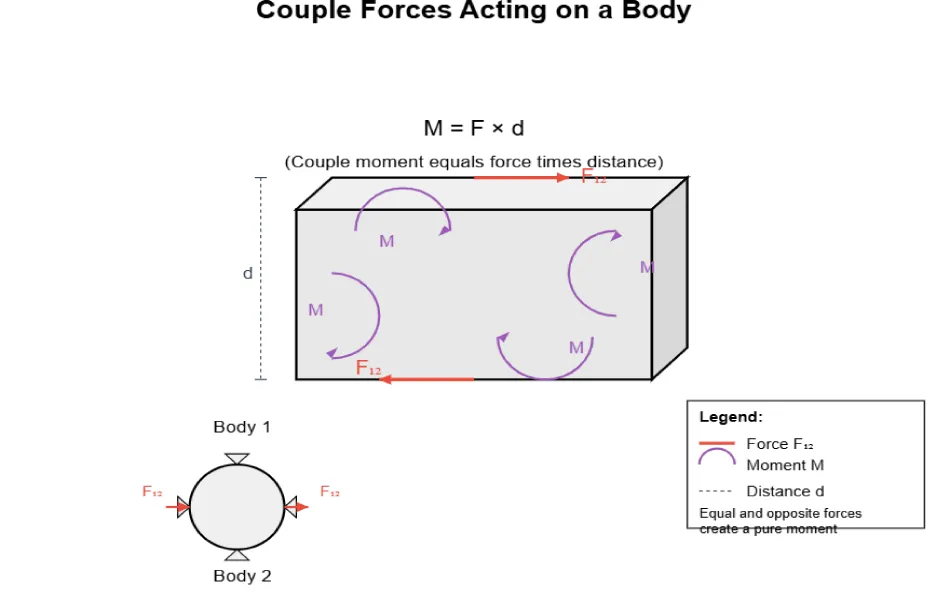
This section highlights the central idea of our hybrid model: while the internal control signal (ISA and pitch) governs the mechanical structure of motion, it is the perceptual layout-visual flow, contact feel, and movement symmetry-that shapes how action is tuned and executed. The visually perceived translation of the club head becomes both a goal and a guide, structuring the motor output without invoking feedback error correction. This concept of motion generation via constrained degrees of freedom finds a mechanical dual in the principle of couple forces, as illustrated in figure 5.
Just as a pair of equal and opposite angular velocities applied at opposing ends of a rigid body yields a pure translational velocity field v = ω × d, a pair of equal and opposite forces F12, applied at a fixed distance d, produces a pure moment M = F × d. These two configurations represent a deep duality in screw theory: the angular motion of a body producing translation, and the linear force on a body producing rotation. In both cases, the internal mechanical state is constrained along a single screw line, and only motion or reaction along that permitted degree of freedom is physically meaningful. During the downswing and impact, the golfer perceptually organizes the swing to afford this invariant translation, by symmetrically generating angular velocities in the upper and lower body that converge into a unified translational path for the clubhead. At impact, this culminates in a perceptually stable, visually guided event where muscle- joint kinesthesis gives way to visual kinesthesis. Thus, the perceptual-motor system is not merely reacting to feedback, but actively recruiting a lawful structure in which vision, force, and motion align under screw-theoretic constraints.
Results
Instantaneous Screw Axis (ISA) trajectories and coordination patterns
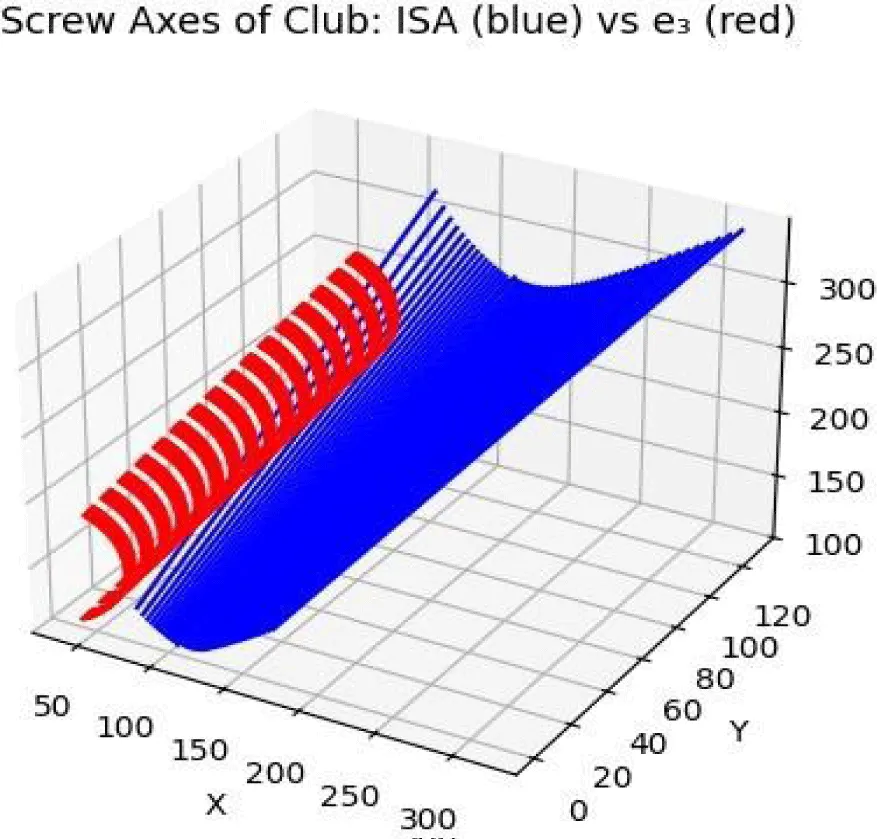
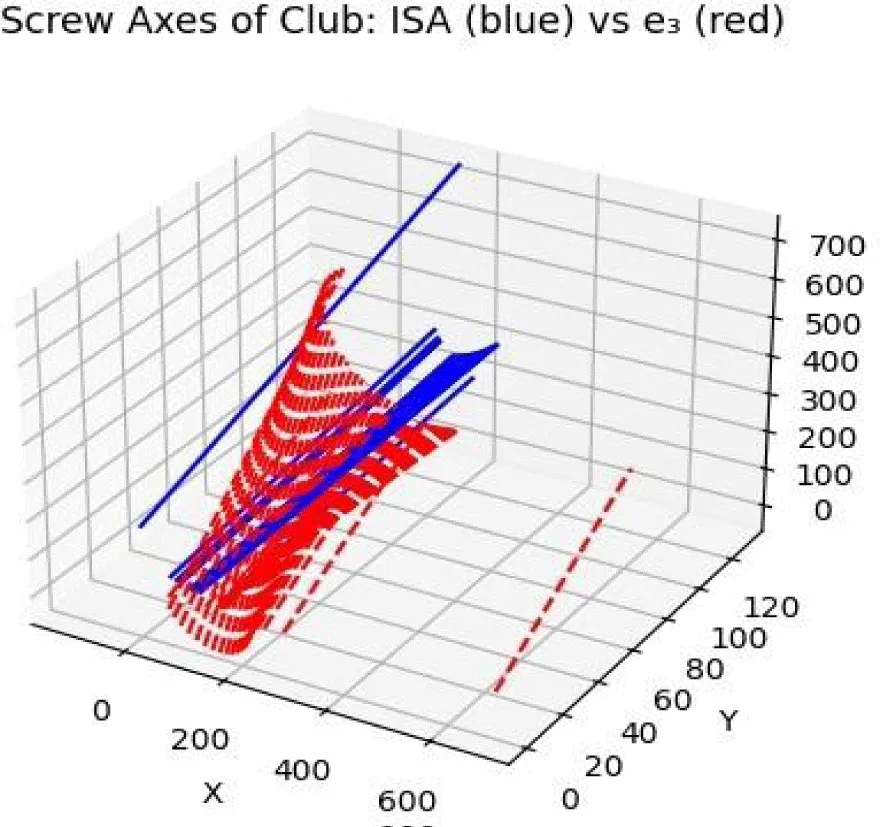
Figures 6,7 present the Instantaneous Screw Axis (ISA) trajectories during the down- swing phase for the proficient and novice golfers, respectively.
In the proficient golfer (Figure 6), the screw axes form a tightly coiled helicoidal structure, indicating a stable and coordinated coupling between angular and linear components of motion. This biomechanical regularity reflects the coherent engagement of multiple body segments-particularly during the downswing-where joint torques are organized to support the delivery of consistent rotational-translational dynamics to the club.
From a perceptual perspective, this ISA organization corresponds to a structured experience: during the downswing, although visual kinesthesis is not yet fully engaged, the haptic system plays a crucial role. Muscle-joint kinesthesis allows the golfer to feel the relative motion of the club to the trunk and limbs. This proprioceptive guidance enables skilled golfers to maintain posture, rhythm, and spatial consistency, helping prepare the system for the final perceptual tuning at impact.
In contrast, the novice golfer (Figure 7) shows dispersed and irregular ISA trajectories, with discontinuities and abrupt directional changes. These variations signal poor mechanical coupling, likely stemming from inconsistent torque generation and a lack of intersegmental timing. Without a coherent mechanical structure, the novice golfer receives fragmented haptic cues-making it difficult to track the club’s motion relative to the body, and leaving the system unprepared for a perceptually coherent impact.
Pitch dynamics and ground reaction force coupling
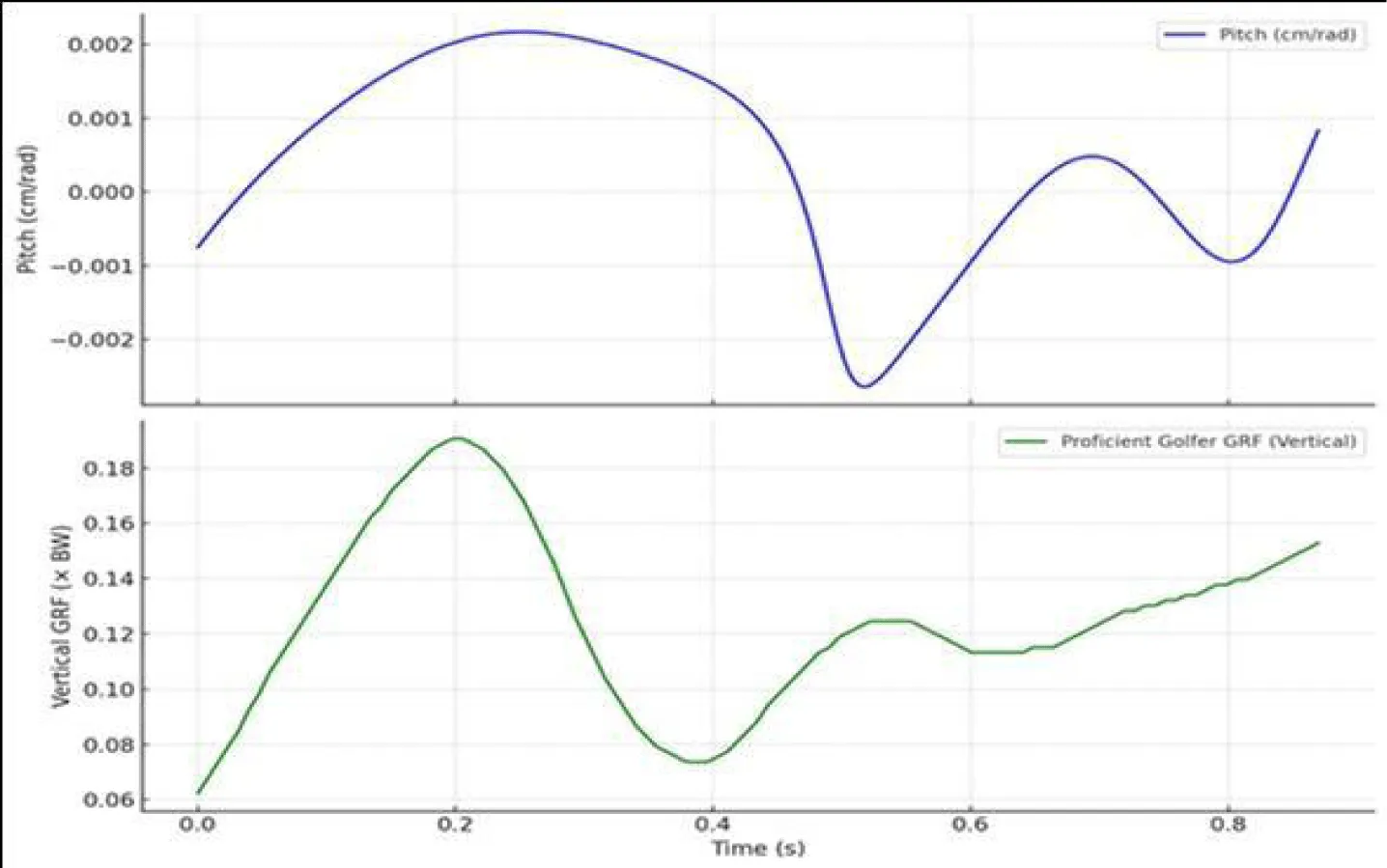
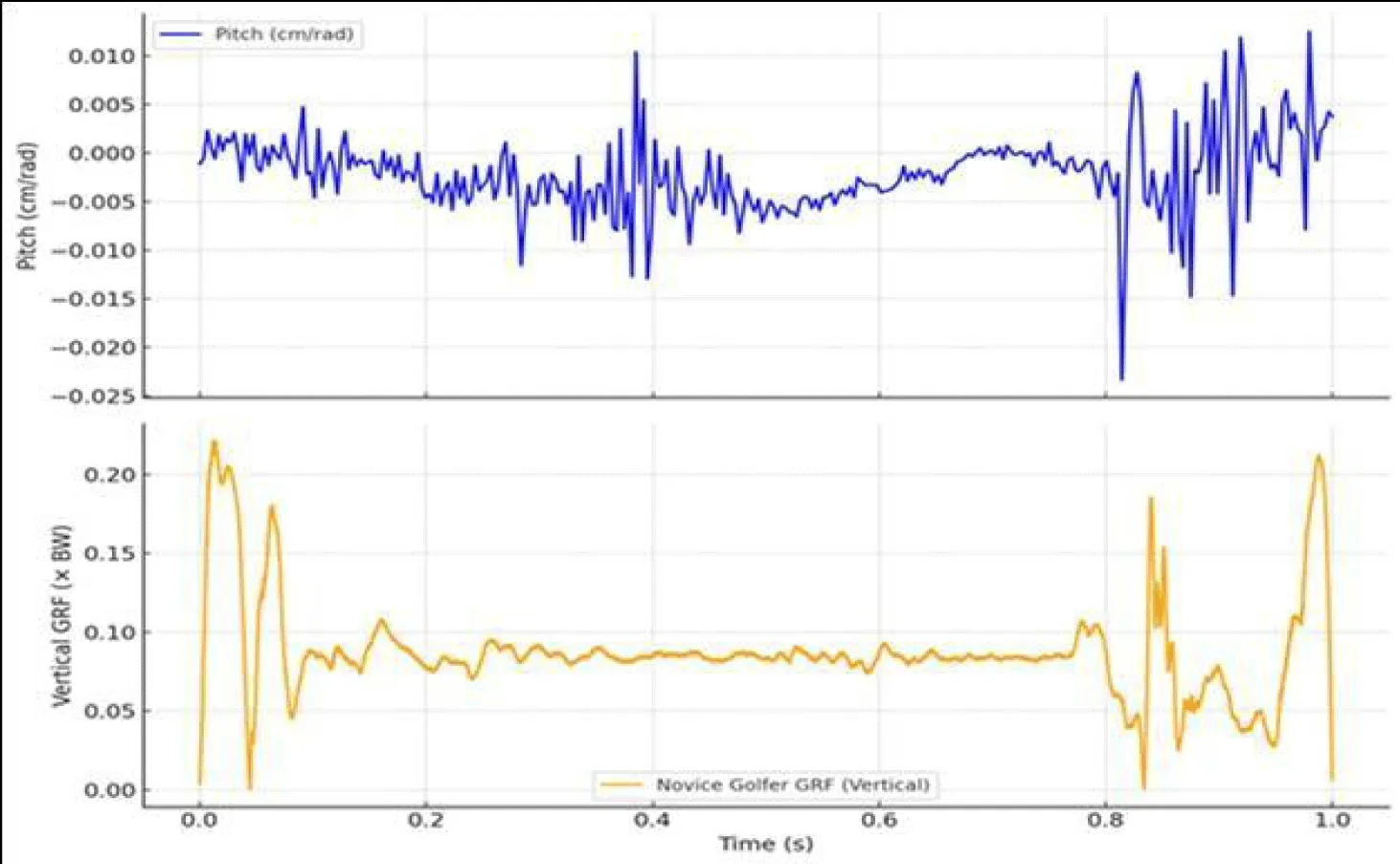
Figures 8 and 9 show synchronized plots of pitch and vertical Ground Reaction Force (GRF) for the two golfers. Pitch, computed as the ratio of translational to angular velocity along the ISA, serves as a key marker of rotational-translational coordination.
In the proficient golfer (Figure 8), pitch remains tightly bounded (±0.0025 cm/rad), oscillating smoothly around zero. This suggests a stable mechanical configuration. During this non-impact phase, the pitch profile reflects a rhythm that can be felt through proprioceptive channels-that is, the golfer can feel how the club’s inertial motion evolves relative to the body’s rotation, without relying on vision.
As the club approaches impact, however, the perceptual mode shifts. The club head’s visually observable displacement becomes paramount. The single, well-timed GRF peak (0.2 s) aligns with the most stable phase of pitch. This alignment provides the golfer with a visual invariant-a perceptually salient translation of the club head-which supports the reliable detection of movement at impact. Here, visual kinesthesis dominates, yielding direct information about the motion of both club and ball relative to the environment.
In the novice golfer (Figure 9), pitch varies unpredictably, with fluctuations from −0.025 to +0.01 cm/rad and multiple sign changes. This instability disrupts not only the mechanical basis of the swing but also its perceptual integrity. The haptic system receives noisy, unstructured feedback, and visual kinesthesis is never given a stable invariant to detect. The GRF pattern, with multiple mistimed peaks, further confirms that internal and external forces are poorly coordinated, resulting in diminished perceptual attunement at impact.
Pitch invariance as a transitional perceptual-motor signature
Our findings reinforce pitch invariance as a biomechanical correlate of perceptual–motor integration. In experts, pitch mediates a sensorimotor transition: during the swing phase, it provides proprioceptive calibration, while at impact, it affords visual invariance of motion. This dual anchoring of pitch-measurable through motion capture and force platforms-marks it as an operational variable linking theory (constraint, conservation) to data.
In proficient golfers, pitch provides continuous proprioceptive feedback during the buildup and becomes a visualized invariant at impact. The club head’s smooth displacement confirms motion direction and timing without requiring internal corrections. For novices, the breakdown of pitch stability removes this perceptual anchor, degrading both proprioceptive and visual integration.
In summary: - The backswing and downswing are guided by haptic feedback-supporting internal calibration of the club-body relation. - The impact phase is governed by visual kinesthesis-detecting the club’s displacement relative to the ball and the environment. - Pitch invariance supports both, offering a continuous, geometry-based signature of perceptual-motor integration.
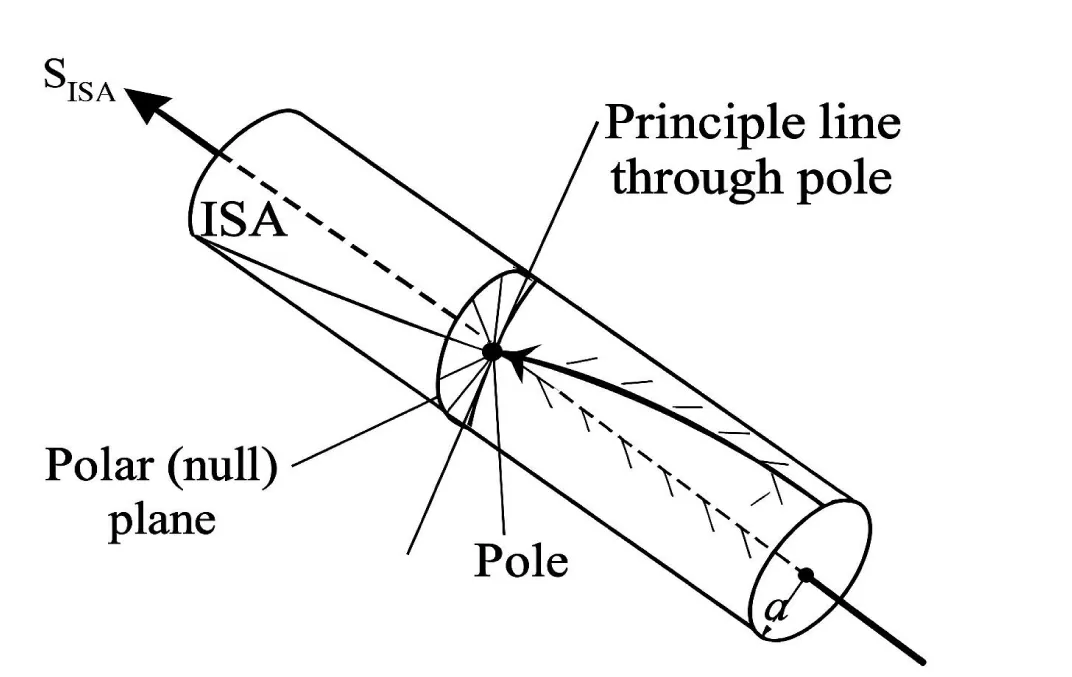
Freedom of one degree is perceived at the moment of impact
- ISA – Instantaneous Screw Axis (axis of constrained motion)
- Pole – Central point where all contact normals converge
- Polar (null) plane – Plane orthogonal to permissible motion, representing con- straint boundary
- Helix – Path traced by a point under screw motion
- Principle line – Axis through the pole along which effective wrench components act
- SISA – Resultant screw representing the allowable twist
- Spokes – Contact normals forming a linear complex; only spokes aligned with ISA contribute to motion
The club head undergoes a screw motion-simultaneous rotation and translation along its instantaneous screw axis (ISA). During this motion, various external forces (e.g., aerodynamic drag, muscular input, or ball impact) may act on the club head. However, only the component of these forces projected along the ISA contributes to the actual screw displacement. The remaining force components do not impede the club head’s screw trajectory. Thus, the field of forces is effectively invariant with respect to the screw motion-whether in the free-flowing phase or at the moment of impact. This illustrates that the perception of freedom in one degree (twist about the ISA) is preserved dynamically and perceptually, providing a stable frame for visual kinesthesis at impact. Figures 3,4 illustrates a foundational concept from screw theory as it applies to skilled movement: when a rigid body-such as a golf club-is constrained to twist about a specific screw axis a, any external wrench (i.e., force–torque pair) acting on it can be equivalently represented by its projection onto that axis. As Phillips (1990) [15] noted, the set of all contact normals converging at a pole resemble the spokes of a wheel and define a linear complex [16]. In this context, the allowable twist of the club occurs along a single “spoke” of this complex, and all effective external wrenches must align with it. This projection ensures that the body’s constrained motion-rotation and translation about a a-remains mechanically and perceptually invariant, even under complex force applications such as impact. This implies that the effect of the ball’s reactive force on the clubface-no matter how complex or distributed-is functionally reduced to its component along the allowable direction of motion.
For the golfer, this projection is not consciously computed but is embedded in the ecological structure of the task. Although the Instantaneous Screw Axis (ISA) itself is not perceived, its kinematic consequences are. The golfer perceives this constraint as a smooth, visually stable translation of the club head at the moment of impact-what Gibson termed visual kinesthesis. This perception of freedom-along a single degree defined by the ISA-is expressed through optic flow rather than internal sensation.
Therefore, the club’s behavior at impact is governed by a mechanical simplification: only motion permitted along the screw axis is effective, and only the portion of the reaction force projected onto that axis produces a result. From the performer’s stand- point, this is experienced not as an abstract vector operation, but as a moment of clarity and perceptual invariance-where force, motion, posture, and visual displacement all converge. The visual registration of displacement thus acts as the ecological indicator of constraint satisfaction, revealing the emergent order of the golfer–club–environment system at its most critical juncture. Figures 3,4 present the trajectories of the Instantaneous Screw Axes (ISAs) for the proficient and novice golfers, respectively. From a biomechanical standpoint, these ISAs represent the dominant directions along which the club–body system twists at each moment during the downswing. According to screw theory, when a rigid body is constrained to move only about a specific screw a, any arbitrary wrench (i.e., external force and torque system) can be represented equivalently by a wrench applied along that same screw, provided its intensity is properly adjusted. This implies that the mechanical effect of the impact-the ball’s reactive force on the club face-is effectively projected onto the dominant ISA at the moment of contact. In this sense, the ISA acts as a mechanical filter, determining which components of the external impulse contribute meaningfully to the resulting motion.
However, while ISAs have mechanical relevance, they are not directly perceived by the performer. That is, the golfer cannot consciously detect or correct the directionality of the ISA during the high-speed dynamics of the swing. Instead, the perceptual system relies on visual kinesthesis-the optic flow generated by the club head’s smooth translational displacement through space. In skilled movement (Figure 3), the ISA trajectories form a coherent helicoidal pattern, allowing the club head to follow a path that visually appears as a pure translation. This apparent translation serves as a perceptual invariant, enabling the golfer to align posture, timing, and effort with the expected impact reaction forces. In other words, while the club–ball interaction produces a reaction force that mechanically aligns with the ISA, the perception of displacement is specified through optic flow, not through force sensation or internal computation.
In contrast, the novice golfer’s ISA pattern (Figure 4) is spatially irregular, disrupting the mechanical projection of impact forces and preventing the emergence of perceptually stable optic flow. Here, neither the reaction force nor the club head’s motion yields consistent information. Without a coherent ISA to structure the force transfer-and without a perceptual invariant in the visual field-the novice performer cannot effectively coordinate posture or force production. In this ecological view, touch, posture, and visual kinesthesis are covariant informational structures, each shaped by but not reducible to the underlying screw dynamics. Skilled movement emerges not from direct control of ISAs but from perceptual attunement to those aspects of the motion that resonate with allowable degrees of freedom and project the relevant dynamics into perceivable forms.
Figure 10 illustrates that external forces-modeled as wrenches-interact only with the screw axis component during swing execution. Thus, measurable force vectors project onto a lower-dimensional constraint space (ISA helicoids), preserving functional degrees of freedom. This mechanical–perceptual synergy provides the golfer with a dynamic experience of “freedom in one degree”-the hallmark of skilled manipulation as theorized.
Discussion
Degrees of freedom and the ecological role of constraint
The central question posed by Bernstein [17]- “How can a neuromuscular system with an exorbitant number of degrees of freedom be made to act as if it had but one?”-guides the theoretical framework of this study. Our findings suggest that pitch invariance and the alignment of the Instantaneous Screw Axis (ISA) serve as ecological constraints that reduce the effective dimensionality of the golfer–environment system. These constraints do not operate in isolation but emerge from the coupling between biomechanical structure and perceptual information.
In the golf swing, the club and body are part of a dynamic system where many Degrees of Freedom (DOF) are available. However, through practice and skill, expert golfers constrain these DOFs into a coherent synergy. This constraint is not enforced by internal computation or command hierarchies but by ecological information [18]: structured in- variants in the visual and haptic flow that prescribe action in real time. Pitch invariance, in particular, acts as a conserved quantity-a marker of biomechanical coherence that remains stable across frames, trials, and task variations.
We therefore propose a duality: DOFs describe the potential for movement, while constraints such as pitch invariance and the orientation of the ISA define lawful regularities that shape actual movement. These constraints emerge from interactions between external force fields (e.g., ground reaction), internal dynamics (e.g., joint torques), and ecological information fields (e.g., optic flow). Thus, control in skilled action is achieved not through micromanagement of variables but through the detection and exploitation of invariant structures.
Pitch and ISA as conserved quantities in skilled manipulation
A core result of this study is the identification of pitch and ISA coherence as conserved quantities-action invariants that persist despite changes in superficial kinematics. These invariants are not merely useful descriptors; they reflect deeper laws governing the percep- tual–motor system, akin to conserved quantities in physics that allow comparison across states of motion. In this sense, our experiment was designed not just to observe biome- chanical differences, but to extract conservation parameters that structure the swing.
In the expert golfer, pitch remains stable and ISA trajectories form helicoidal pat- terns-suggesting that the system has discovered an invariant under constraint. This aligns with Gibson’s concept of information as specificity rather than uncertainty. That is, skilled performance arises not by eliminating variability, but by constraining it into lawful transformations. Conversely, the novice golfer exhibits disrupted pitch profiles and disorganized ISAs, reflecting a system not yet attuned to the ecological invariants available in the environment.
From this perspective, pitch invariance and ISA stability do more than characterize expert performance-they offer an ecological solution to Bernstein’s problem. Through the coupling of organismic and environmental forces via perceptual invariants, the system achieves control by effectively reducing the number of actionable degrees of freedom. Vi- sual kinesthesis [7,8,19], operating as a field of structured optic flow, provides a perceptual substrate through which these constraints are realized and enacted.
Conclusion
This study advances a new understanding of the golf swing by integrating biomechanical invariants with ecological principles of perception. While pitch invariance serves as a measurable signature of biomechanical coherence, it does not arise from internal correction mechanisms applied to control variables such as the Instantaneous Screw Axis (ISA). Instead, skilled movement emerges from the continuous alignment of the body with structured information in the environment.
From the initial setup through the backswing, downswing, and final impact, the golfer maintains a continuous transformation of the optic array. This unfolding stream of structured visual information constitutes visual kinesthesis-the perception of one’s own motion relative to the environment through optic flow. Unlike traditional feedback control, which relies on retrospective error correction, visual kinesthesis operates in a feed forward and ecological manner. It enables the golfer to attune movement in real time to environmental affordances such as the contour of the ball, the slope of the terrain, and the perceptual rhythm of motion.
In skilled performance, visual kinesthesis becomes a stabilizing perceptual field that guides the club toward impact, transforming the complex dynamics of manipulation into a visually grounded and embodied act. By recognizing the primacy of vision in guid- ing action-not merely detecting error-we offer a new foundation for understanding manipulation, learning, and expertise in sports and beyond.
This approach moves us toward a new understanding of motor skill-not as the repetition of learned commands, but as the real-time exploitation of constraints and conserved patterns. The golf swing thus becomes a paradigm case for studying how ecological information sculpts movement, offering a scalable model for perception-action coupling across skilled tasks.
Acknowledgments
The authors would like to acknowledge Miwon Kim, Sofia Camacho, and Jorge Infante for their help during data acquisition for this study. The first author would also like to thank Sangdo Kim for his stimulating discussions regarding the perfection of the golf swing.
This research was funded by PROCIENCIA under contract No PE501080681-2022- PRO-CIENCIA, Proyectos Especiales: Proyectos de Investigadores Visitantes.
References
- Cornelius Lanczos. The variational principles of mechanics. Courier Corporation, 2012.
- Teu KK, Kim W, Fuss FK, Tan J. The analysis of golf swing as a kinematic chain using dual Euler angle algorithm. J Biomech. 2006;39(7):1227-38. doi: 10.1016/j.jbiomech.2005.03.013. Epub 2005 Jun 2. PMID: 15936026.
- Koon Teu, Wangdo Kim, John Tan, Franz Fuss. Using dual euler angles for the analysis of arm movement during the badminton smash. Sports Engineering. 2005;8(3):171-178. doi: 10.1007/BF02844017.
- RS Ball. A treatise on the theory of screws. Cambridge University Press; 1900.
- K H Hunt. Kinematic geometry of mechanism. Clarendon Press, Oxford; 1990.
- JK Davidson, KH Hunt. Robots and screw theory: Applications of kinematics and statics to robotics. Oxford University Press; 2004.
- GIBSON JJ. Visually controlled locomotion and visual orientation in animals. Br J Psychol. 1958 Aug;49(3):182-94. doi: 10.1111/j.2044-8295.1958.tb00656.x. PMID: 13572790.
- JJ Gibson. The ecological approach to visual perception. Houghton Mifflin; 1979.
- Kim W, Kohles SS. A reciprocal connection factor for assessing knee-joint function. Comput Methods Biomech Biomed Engin. 2012;15(9):911-7. doi: 10.1080/10255842.2011.566270. Epub 2011 May 24. PMID: 21491255.
- Wangdo Kim, Antonio Veloso, Duarte Arau´jo, Maria Machado, Veronica Vleck, Lil- iana Aguiar, Silvia Cabral, Filomena Vieira. Haptic perception-Action coupling manifold of effective golf swing. International Journal of Golf Science. 2013;2(1):10-32.
- David M Trujillo, Henry R Busby. Practical inverse analysis in engineering. CRC press; 1997:7.
- Richard Bellman. Introduction to the mathematical theory of control processes: Lin- ear equations and quadratic criteria. Elsevier. 2016.
- Kim W, Espanha MM, Veloso AP, Araújo D, João F, Carrão L, Kohles SS. An Informational Algorithm as the Basis for Perception-Action Control of the Instantaneous Axes of the Knee. J Nov Physiother. 2013 Mar 27;3(1):127. doi: 10.4172/2165-7025.1000127. PMID: 24932433; PMCID: PMC4057049.
- Jack Phillips. Freedom in machinery. Cambridge University Press; 2007:1.
- David B Dooner, Ali Seireg. The kinematic geometry of gearing: A concurrent engineering approach. John Wiley & Sons; 1995:3.
- Charles Minshall Jessop. A treatise on the line complex. University Press; 1903.
- Nikolai A Bernstein. The problem of interrelation between coordination and local- ization. Arch Biol Sci. 1935;38:1-35.
- Robert E Shaw, MT Turvey. Ecological foundations of cognition. ii: Degrees of freedom and conserved quantities in animal-environment systems. Journal of Consciousness Studies. 1999;6(11-12):111-124.
- JJ Gibson. The senses considered as perceptual systems. Houghton, Boston, 1966.
Content Alerts
SignUp to our
Content alerts.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.