Dynamics of Leukemia Models

Millions of people are affected by leukemia. It is important to understand the progression dynamics of this disease to be able to minimize the damage that is caused by it. This article provides a mathematical framework to develop strategies to control leukemia. Bifurcation analysis is a powerful mathematical tool used to deal with the nonlinear dynamics of any process. Several factors must be considered, and multiple objectives must be met simultaneously. Bifurcation analysis and Multiobjective Nonlinear Model Predictive Control (MNLMPC) calculations are performed on three leukemia models. The MATLAB program MATCONT was used to perform the bifurcation analysis. The MNLMPC calculations were performed using the optimization language PYOMO in conjunction with the state-of-the-art global optimization solvers IPOPT and BARON. The bifurcation analysis revealed the existence of limit points and branch in the models. The limit and branch points were beneficial because they enabled the multiobjective nonlinear model predictive control calculations to converge to the Utopia point in both problems, which is the most beneficial solution. A combination of bifurcation analysis and multiobjective nonlinear model predictive control for leukemia models is the main contribution of this paper.

Deininger MW, et al. [1] investigated the molecular biology of chronic myeloid leukemia. Topaly J, et al. [2] researched the synergistic activity of the new ANL-specific tyrosine kinase inhibitor STI571 and the effect of chemotherapeutic drugs on BCR-ABL-positive chronic myelogenous leukemia cells. Deininger MW and co-workers [3,4] studied the effect of imatinib on patients with chronic myeloid leukemia. Goldman JM, et al. [5] described the treatments for chronic myeloid leukemia patients. Mackey MC, et al. [6] studied the periodic behavior of chronic myelogenous leukemia. Baccarani M, et al. [7] studied the effect of Imatinib and pegylated human recombinant interferon-alpha2 b on early chronic-phase chronic myeloid leukemia. Moore H, et al. [8] developed a mathematical model of chronic myelogenous leukemia. Adimy M, et al. [9] performed a mathematical study of the hematopoiesis process with applications to chronic myelogenous leukemia. Michor F, et al. [10], studied the dynamics of chronic myeloid leukemia. Nanda S, et al. [11], performed single objective optimal control of a mathematical model of chronic myelogenous leukemia. Liso A, et al. and Ommen HB, et al. [12,13] and Cucuianu A, et al. [14] performed theoretical studies of mathematical models involving myelogenous leukemia. Dohner H, et al. [15] provided recommendations for the diagnosis and management of acute myeloid leukemia in adults. Komarova NL. [16], Stiehl T, et al. [17], Maclean AL, et al. [18,19], Agarwal M, et al. [20], and Clapp G, et al. [21] performed mathematical investigations of problems involving leukaemia. Crowell HL, et al. [22] studied feedback mechanisms control coexistence in a stem cell model of acute myeloid leukaemia. Austin R, et al. [23], described harnessing the immune system in acute myeloid leukaemia. Zeidan AM, et al. [24] described the economic burden associated with acute myeloid leukemia treatment. Masarova L, et al. [25] performed additional investigations about harnessing the immune system against leukemia. Lichtenegger FS, et al. [26] presented more developments in immunotherapy of acute myeloid leukemia. Krupar R, et al. [27], provided an analysis of anti-leukemia immune response and immune evasion in acute myeloid leukemia. Sharp JA, et al. [28] and Khatun MS, et al. [29] performed single-objewctive optimal control studies of ,myeloid leukaemia treatment , Journal of Theoretical Biology, Volume 470, 2019, Pages 30-42, ISSN 0022-5193. In this work, bifurcation analysis is performed in conjunction with Multiobjective Nonlinear Model Predictive Control (MNLMPC) for three leukemia models that are described in Nanda S, et al. [11] , Khatun MS, et al. [29] and Sharp JA, et al. [28] (Model 1, Model 2, and Model 3). This paper is organized as follows. First, the leukemia models are presented. The numerical procedures (Bifurcation Analysis and Multiobjective Nonlinear Model Predictive Control (MNLMPC) are then described. This is followed by the results and discussion, and conclusions.

Model 1

The model equations are

$\begin{array}{l}\frac{d{T}_n}{dt}=sn-u2(dn{T}_n)-\frac{kn{T}_n(c)}{c+\eta }\\ \frac{d{T}_e}{dt}=\alpha n\frac{kn{T}_n(c)}{c+\eta }+\alpha e\frac{kn{T}_e(c)}{c+\eta }-u2(de{T}_e)-{\gamma }_{e}C(T_e)\text{ (1)}\\ \frac{dC}{dt}=(1-u1)r_{c}C\ln (\frac{C_{\max }}{C})-u2(dcC)-{\gamma }_{c}C(T_e)\end{array}$

Here $(T_n,T_e,C)$ represent the naive T cell population and the effector T cell population and the cancer cell population, respectively.The base values of the parameters are sn = 0.29; dn = 0.35; de = 0.40; dc = 0.012; kn = 0.066; $\eta$ = 140; ${\alpha }_n$ = 0.39; ${\alpha }_e$ = 0.65; Cmax = 16000; rc = 0.011; ${\gamma }_e$ = 0.079; ${\gamma }_c$ = 0.058. u1 and u2 are the bifurcation and control parameters. The naive T cells, upon encountering antigens from cancer cells, differentiate into effector T cells that target and destroy the tumor. However, cancer can also negatively impact naive T cells, potentially impairing their function or even causing their death, which can hinder the body's ability to fight the cancer. The negative terms in the differential equations indicate this fact.

Model 2

$\begin{array}{l}\frac{d(Sval)}{dt}=A-{\alpha }_0(Sval)-\beta (Sval(Ival)-u1Sval\hfill \\ \frac{d(Ival)}{dt}=\beta (Sval(Ival)-\left({\beta }_0+\alpha \right)Ival-\left(u2(Ival\right))\hfill \\ \frac{d(Wval)}{dt}=\alpha \left(Ival\right)-b0(Wval)+u1(Sval)+u2(Ival)\hfill \end{array}\text{ (2)}$

Here Sval, Ival, Wval represent susceptible cells, infected cells and immune cells. The base values of the parameters are A = 1.5; ${\alpha }_0$ = 0.01; $\beta$ = 0.0005; ${\beta }_0$ = 0.003; $\alpha$ = 0.0001;b0 = 0.03. u1 and u2 are the bifurcation and control parameters.

Model 3

The model equations are

$\begin{array}{l}\frac{d(Sval)}{dt}={\rho }_{s}Sval\left(k1-sval\right)-{\delta }_s(Sval);\hfill \\ \frac{d(Aval)}{dt}={\delta }_s(Sval)-{\delta }_a(Aval)+{\rho }_{a}Aval\left(k2-\left(Aval+Lval\right)\right);\hfill \\ \frac{d(Dval)}{dt}={\rho }_{a}Aval-{\mu }_{d}Dval\hfill \\ \frac{d(Lval)}{dt}=-{\delta }_l(Lval)+{\rho }_{l}Lval\left(k2-\left(Aval+Lval\right)\right)\mathrm{...}\hfill \\ -\frac{\alpha Lval}{\left(\gamma +Lval\right)}-\left(u(Lval\right));\hfill \\ \frac{d(Tval)}{dt}={\delta }_l(Lval)-{\mu }_{t}Tval\hfill \end{array}\text{ (3)}$

Here $(Sval,Aval,Dval,Lval,Tval)$ represent haematopoietic stem cells, progenitor cells, terminally differentiated cells, leukaemia stem cells, and fully differentiated leukaemia cells.

The base parameter values are

${\rho }_s$ = 0.5; ${\rho }_a$ = 0.43; ${\rho }_l$ = 0.27; ${\delta }_s$ = 0.14; ${\delta }_a$ = 0.44; ${\delta }_l$ = 0.05; ${\mu }_d$ = 0.275; ${\mu }_t$ = 0.3; k1 = 1; k2 = 1;

$\alpha$ = 0.015; $\gamma$ = 0.01. u is the bifurcation parameter and control variable.

The MATLAB software MATCONT is used to perform the bifurcation calculations. Bifurcation analysis deals with multiple steady-states and limit cycles. Multiple steady states occur because of the existence of branch and limit points. Hopf bifurcation points cause limit cycles . A commonly used MATLAB program that locates limit points, branch points, and Hopf bifurcation points is MATCONT Dhooge A, et al. [30]; Dhooge AW, et al. [31]. This program detects Limit Points(LP), Branch Points(BP), and Hopf bifurcation points(H) for an ODE system

$\frac{dx}{dt}=f(x,\alpha )\text{ (3)}$

$x\in R^n$ Let the bifurcation parameter be $\alpha$ Since the gradient is orthogonal to the tangent vector,

The tangent plane at any point $w=[w_1,w_2,w_3,w_4,\mathrm{....}{w}_{n+1}]$ must satisfy

$Aw=0\text{ (4)}$

where A is

$A=[\partial f/\partial x|\partial f/\partial \alpha ]\text{ (5)}$

where $\partial f/\partial x$ is the Jacobian matrix. For both limit and branch points, the matrix $[\partial f/\partial x]$ must be singular. The n+1 th component of the tangent vector $w_{n+1}$ = 0 for a Limit Point (LP) and for a Branch Point (BP) the matrix $\left[\begin{array}{l}A\\ w^T\end{array}\right]$ must be singular. At a Hopf bifurcation point,

$\det (2f_x(x,\alpha )@I_n)=0\text{ (6)}$

@ indicates the bialternate product while $I_n$ is the n-square identity matrix. Hopf bifurcations cause limit cycles and should be eliminated because limit cycles make optimization and control tasks very difficult. More details can be found in Kuznetsov YA. [32,33] and Govaerts WJF. [34].

Flores Tlacuahuaz A. [35] developed a Multiobjective Nonlinear Model Predictive Control (MNLMPC) method that is rigorous and does not involve weighting functions or additional constraints. This procedure is used for performing the MNLMPC calculations Here ${\displaystyle \sum _{t_{i=0}}^{t_i=t_f}{q}_j(t_i)}$ (j = 1, 2..n) represents the variables that need to be minimized/maximized simultaneously for a problem involving a set of ODE

$\frac{dx}{dt}=F(x,u)\text{ (7)}$

$t_f$ Being the final time value, and n the total number of objective variables and. u the control parameter. This MNLMPC procedure first solves the single objective optimal control problem independently optimizing each of the variables ${\displaystyle \sum _{t_{i=0}}^{t_i=t_f}{q}_j(t_i)}$ individually. The minimization/maximization of ${\displaystyle \sum _{t_{i=0}}^{t_i=t_f}{q}_j(t_i)}$ will lead to the values $q_j^{*}$ . Then the optimization problem that will be solved is

$\begin{array}{l}\min ({\displaystyle \sum _{j=1}^n({\displaystyle \sum _{t_{i=0}}^{t_i=t_f}{q}_j(t_i)}-q_j^{*}){)}^2}\text{ (8)}\\ subjectto\frac{dx}{dt}=F(x,u);\end{array}$

This will provide the values of u at various times. The first obtained control value of u is implemented and the rest are discarded. This procedure is repeated until the implemented and the first obtained control values are the same or if the Utopia point

where ( ${\displaystyle \sum _{t_{i=0}}^{t_i=t_f}{q}_j(t_i)}=q_j^{*}$ for all j) is obtained.

Pyomo (Hart, et al. [36] is used for these calculations. Here, the differential equations are converted to a Nonlinear Program (NLP) using the orthogonal collocation method The NLP is solved using IPOPT (Wächter A, et al. [37] and confirmed as a global solution with BARON Tawarmalani M, et al. [38].

The steps of the algorithm are as follows

Optimize ${\displaystyle \sum _{t_{i=0}}^{t_i=t_f}{q}_j(t_i)}$ and obtain $q_j^{*}$ at various time intervals t_i. The subscript i is the index for each time step.

Minimize $({\displaystyle \sum _{j=1}^n({\displaystyle \sum _{t_{i=0}}^{t_i=t_f}{q}_j(t_i)}-q_j^{*}){)}^2}$ and get the control values for various times.

Implement the first obtained control values

Repeat steps 1 to 3 until there is an insignificant difference between the implemented and the first obtained value of the control variables or if the Utopia point is achieved. The Utopia point is when ${\displaystyle \sum _{t_{i=0}}^{t_i=t_f}{q}_j(t_i)}=q_j^{*}$ for all j.

Sridhar LN. [39] proved that the MNLMPC calculations to converge to the Utopia solution when the bifurcation analysis revealed the presence of limit and branch points. This was done by imposing the singularity condition on the co-state equation Upreti SR. [40]. If the minimization of $q_1$ lead to the value $q_1^{*}$ and the minimization of $q_2$ lead to the value $q_2^{*}$ The MNLPMC calculations will minimize the function ${(q_1-q_1^{*})}^2+{(q_2-q_2^{*})}^2$ . The multiobjective optimal control problem is

$\begin{array}{l}\min {(}^{q_1}+{(}^{q_2}\text{ (9)}\\ subjectto\frac{dx}{dt}=F(x,u)\end{array}$

Differentiating the objective function results in

$\begin{array}{l}\frac{d}{d{x}_i}({(}^{q_1}+{(}^{q_2})=\text{ (10)}\\ 2(q_1-q_1^{*})\frac{d}{d{x}_i}(q_1-q_1^{*})+\\ 2(q_2-q_2^{*})\frac{d}{d{x}_i}(q_2-q_2^{*})\end{array}$

The Utopia point requires that both $(q_1-q_1^{*})$ and $(q_2-q_2^{*})$ are zero. Hence

$\frac{d}{d{x}_i}({(q_1-q_1^{*})}^2+{(q_2-q_2^{*})}^2)=0\text{ (11)}$

the optimal control co-state equation (Upreti; 2013) is

$\begin{array}{l}\frac{d}{dt}({\lambda }_i)=-\frac{d}{d{x}_i}({(}^{q_1}+\\ {(}^{q_2})-f_x{\lambda }_i;{\lambda }_i(t_f)=0\text{ (12)}\end{array}$

${\lambda }_i$ is the Lagrangian multiplier. $t_f$ is the final time. The first term in this equation is 0 and hence

$\frac{d}{dt}({\lambda }_i)=-f_x{\lambda }_i;{\lambda }_i(t_f)=0\text{ (13)}$

At a limit or a branch point, for the set of ODE $\frac{dx}{dt}=f(x,u)$ $f_x$ is singular. Hence there are two different vectors-values for $[{\lambda }_i]$ where $\frac{d}{dt}({\lambda }_i)>0$ and $\frac{d}{dt}({\lambda }_i)<0$ . In between there is a vector $[{\lambda }_i]$ where $\frac{d}{dt}({\lambda }_i)=0$ . This coupled with the boundary condition ${\lambda }_i(t_f)=0$ will lead to $[{\lambda }_i]=0$ This makes the problem an unconstrained optimization problem, and the only solution is the Utopia solution.

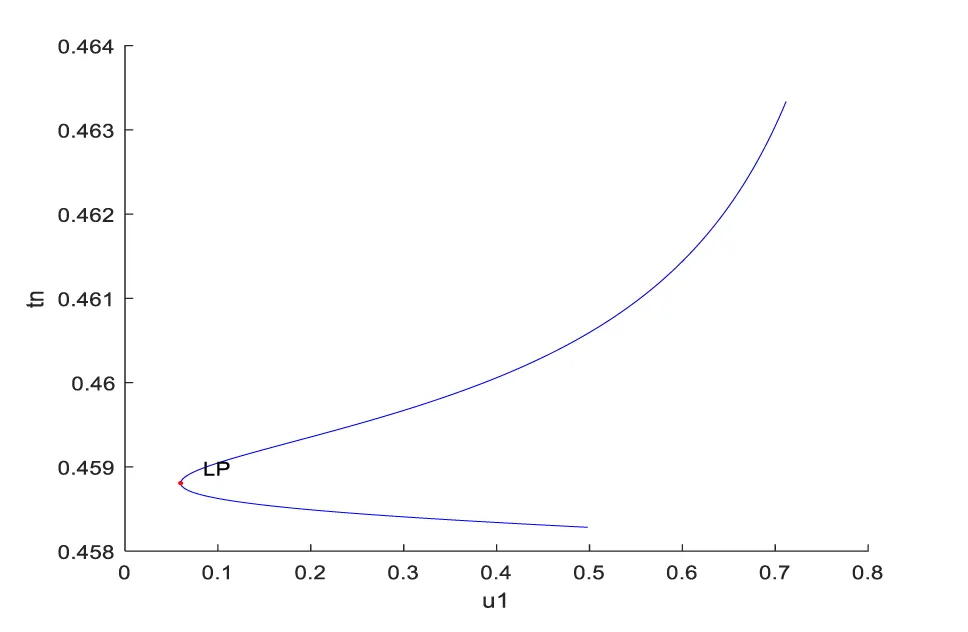
For the bifurcation analysis of model 1, u1 is the bifurcation parameter and the other parameter values are sn = 0.29; dn = 0.35; de = 0.40; dc = 0.012; kn = 0.066; $\eta$ = 0.0020; ${\alpha }_n$ = 0.39; ${\alpha }_e$ = 0.65; Cmax = 16000; rc = 0.011; ${\gamma }_e$ = 0.079; ${\gamma }_c$ = 0.158; u2 = 1.62; a limit point was found at $[T_n,T_e,C,u1]$ values of (0.458808 0.639024 0.140437 0.059894 ). This is shown in figure 1a.

Figure 1a: Bifurcation analysis model 1 u1 is bifurcation parameter.

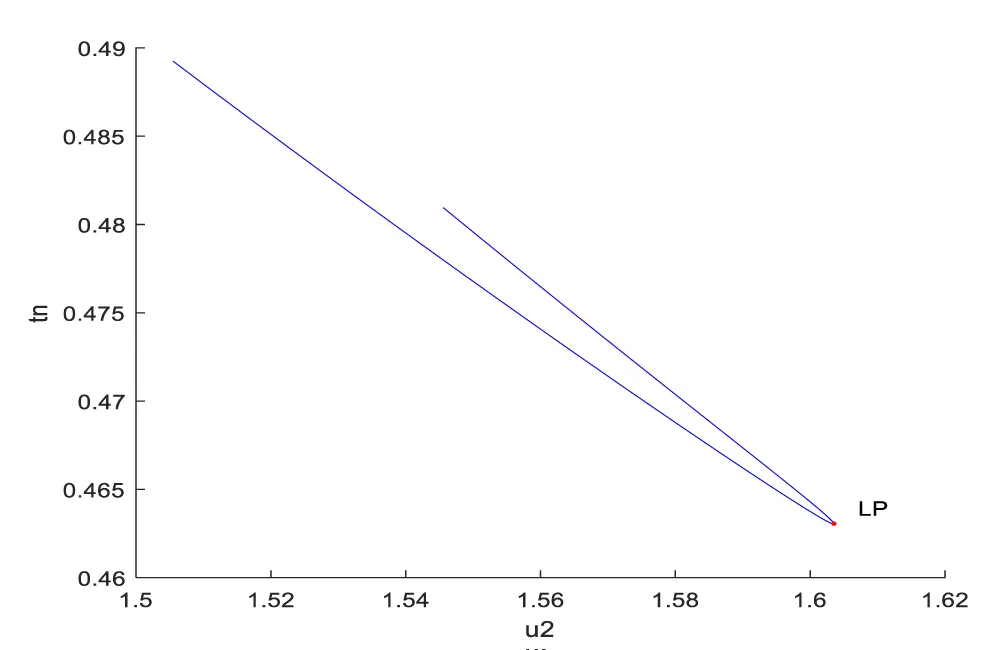
When u2 is the bifurcation parameter and the other parameter values a reSn = 0.29; dn = 0.35; de = 0.40; dc = 0.012; kn = 0.066; $\eta$ = 0.0020; ${\alpha }_n$ = 0.39; ${\alpha }_e$ = 0.65; Cmax = 16000; rc = 0.011; ${\gamma }_e$ = 0.079; ${\gamma }_c$ = 0.1; u1 = 0.059894; a limit point was found at $[T_n,T_e,C,u2]$ values of (0.463059 1.015647 0.135093 1.603523). This is shown in figure 1b.

Figure 1b: Bifurcation analysis model 1 u2 is bifurcation parameter.

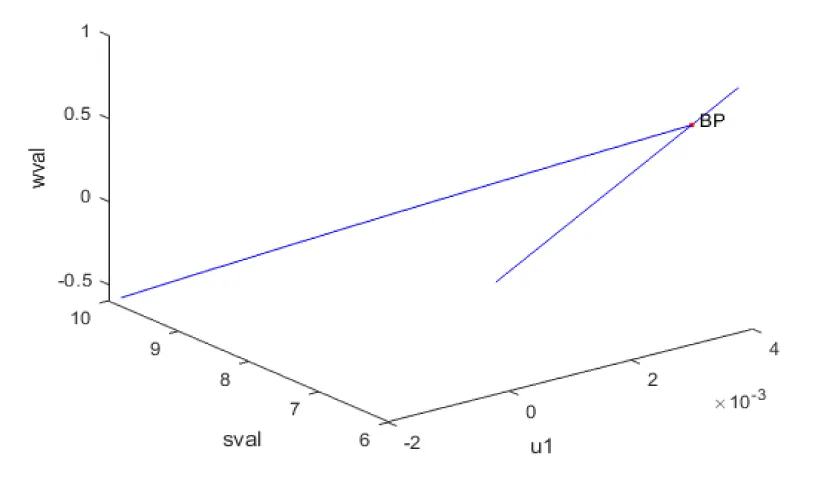
For the bifurcation analysis of model 2, when u1 is the bifurcation parameter and the other parameter values are

A = 0.082; ${\alpha }_0$ = 0.01; $\beta$ = 0.0005; ${\beta }_0$ = 0.003; $\alpha$ =0.0001; b0 = 0.03; u2 = 0;

A branch point occurred at [sval, ival, wval, u1] values of (6.200000 0.000000 0.666667 0.003226). This is shown in figure 2a.

Figure 2a: Bifurcation analysis model 2 u1 is bifurcation parameter.

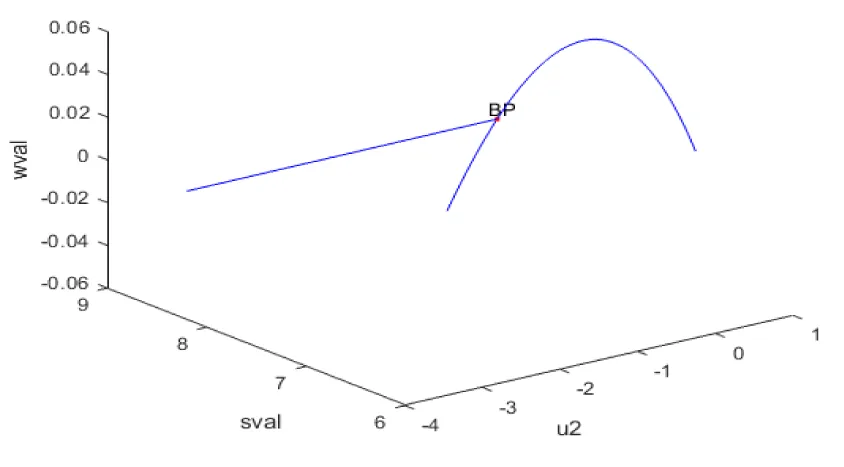
When u2 is the bifurcation parameter and the other parameter values are

A = 0.082; ${\alpha }_0$ = 0.01; $\beta$ = 0.0005; ${\beta }_0$ = 0.003; $\alpha$ = 0.0001; b0 = 0.03; u1 = 0;

A branch point occurred at [sval, ival, wval, u2] values of (8.200000 0.0 0.0 0.0010). This is shown in figure 2b.

Figure 2b: Bifurcation analysis model 2 u2 is bifurcation parameter.

For the bifurcatiom analysis of model 3, u is the bifurcation parameter and the other parameter values are

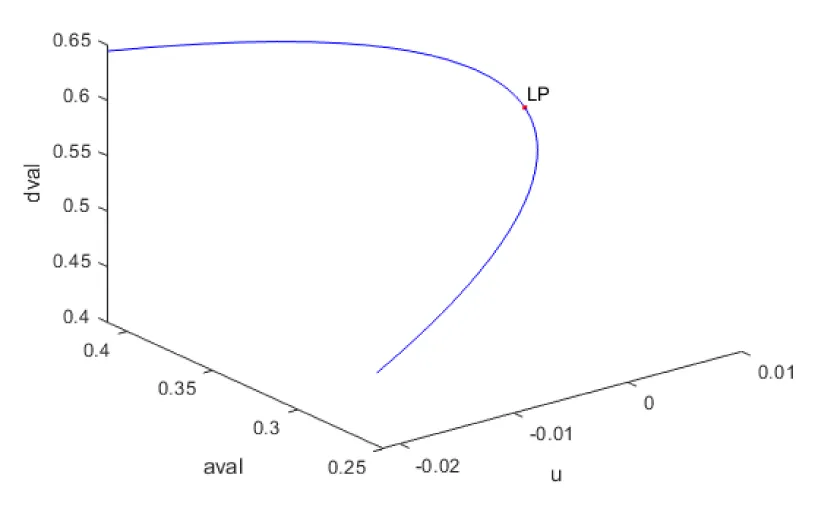
${\rho }_s$ = 0.5; ${\rho }_a$ = 0.43; ${\rho }_l$ = 0.27; ${\delta }_s$ = 0.14; ${\delta }_a$ = 0.44; ${\delta }_l$ = 0.04; ${\mu }_d$ = 0.275; ${\mu }_t$ = 0.3; k1 = 1; k2 = 1; $\alpha$ = 0.015; $\gamma$ = 0.01; a limit point at [sval;aval;dval;lval;tval,u] values of ( 0.72 0.354939 0.554995 0.282254 0.037634 0.006633 ). This is shown in figure 3.

Figure 3: Bifurcation analysis model 3u is bifurcation parameter.

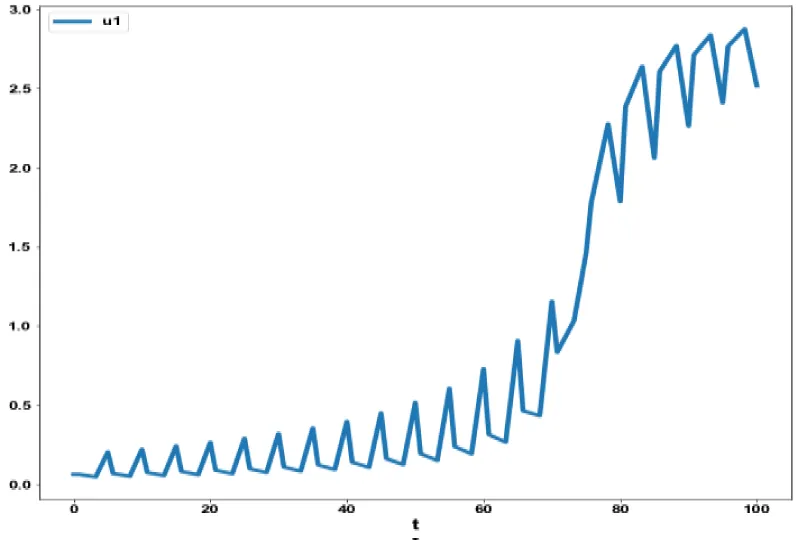
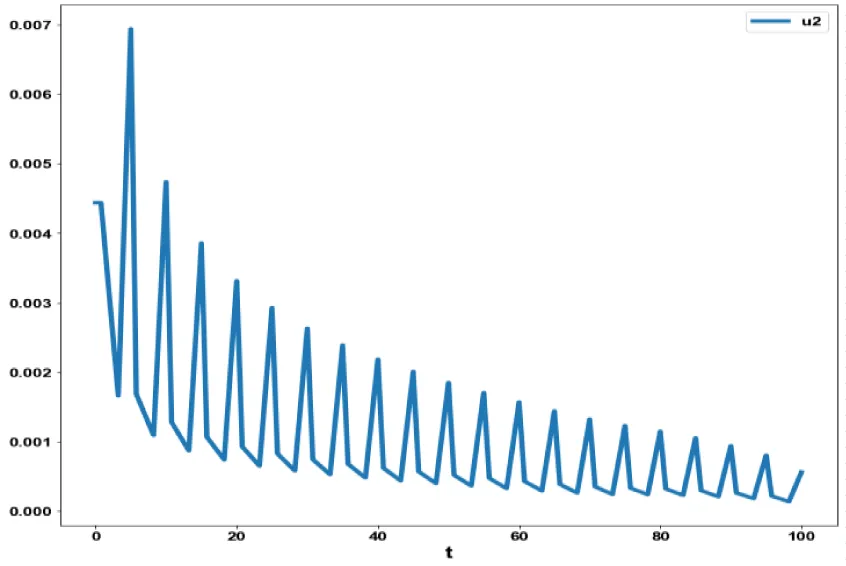
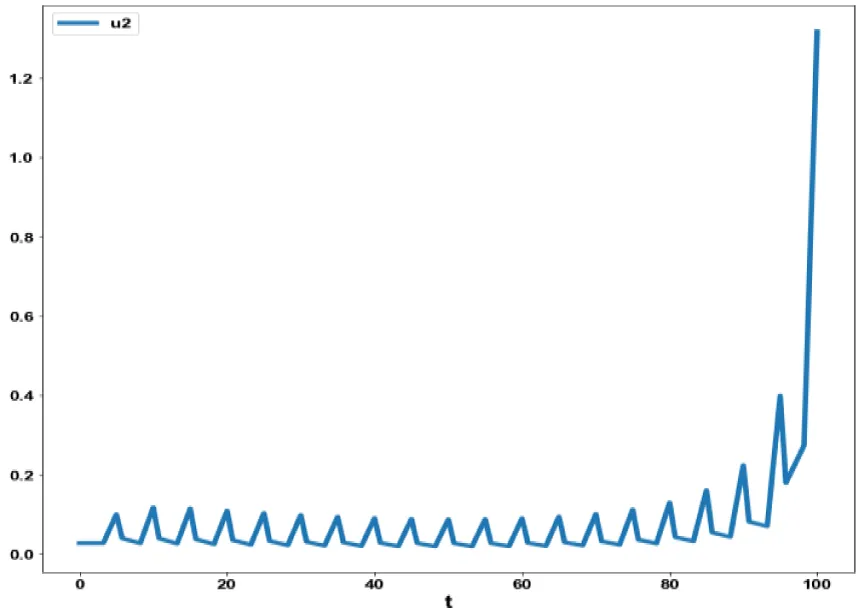
For the MNLMPC calculations involving model 1, ${\displaystyle \sum _{t_{i=0}}^{t_i=t_f}c(t_i)}$ was minimized ${\displaystyle \sum _{t_{i=0}}^{t_i=t_f}{T}_n(t_i)}$ was maximized individually and resulted in values of 0 and 2000. The overall optimal control problem will involve the minimization of ${({\displaystyle \sum _{t_{i=0}}^{t_i=t_f}c(t_i)}-0)}^2+{({\displaystyle \sum _{t_{i=0}}^{t_i=t_f}{T}_n(t_i)}-2000)}^2$ was minimized subject to the equations governing the model. This led to a value of zero (the Utopia solution. The various concentration profiles for this MNLMPC calculation are shown in figures 4a-c. (Figures 4a-c) indicate the variation of tn, te and c versus time.

Figure 4a: MNLMPC for model 1 tn vs t.

Figure 4b: MNLMPC for model 1 te vs t.

Figure 4c: MNLMPC for model 1 c vs t.

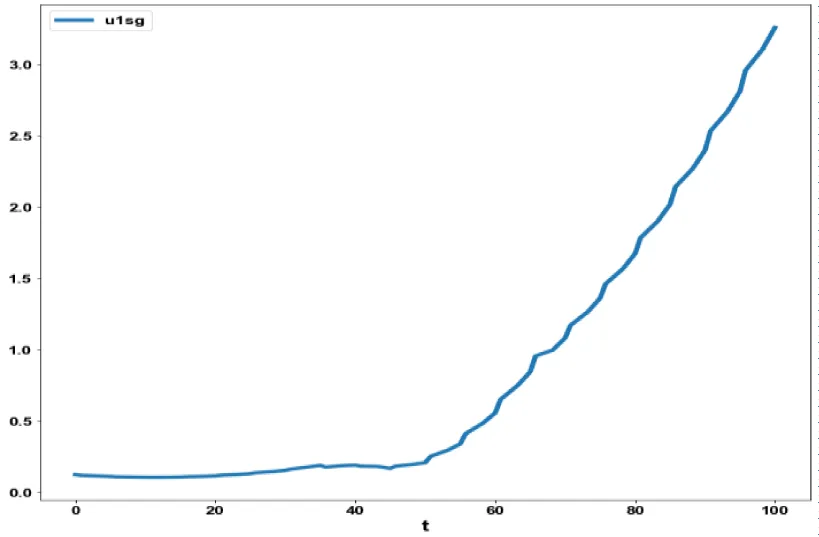
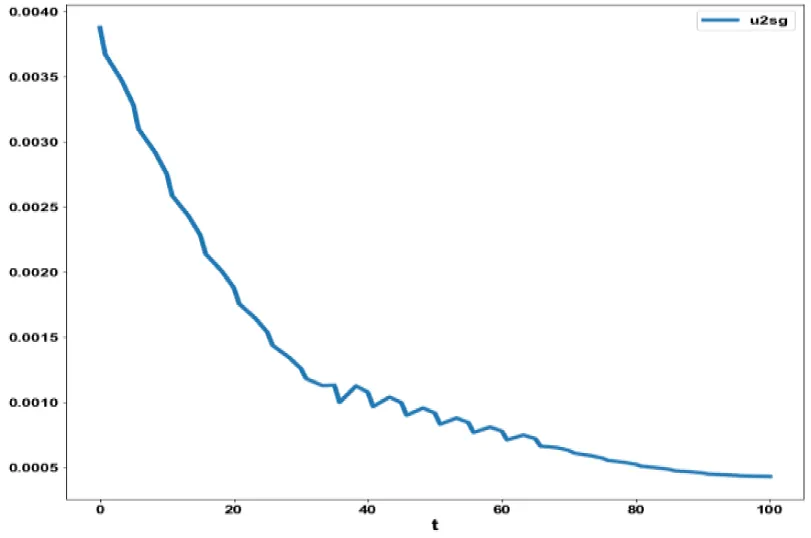
The obtained control profile of u1 and u2 exhibited noise (Figures 4d, e). This issue was addressed using the Savitzky-Golay Filter. The smoothed version of this profile is shown in figures 4f, g. The MNLMPC control values obtained for u1 and u2 are 0.0624 and 0.00443. The MNLMPC calculations converged to the Utopia solution, validating the analysis by Sridhar LN. [39], which demonstrated that the presence of a limit point/branch point enables the MNLMPC calculations to reach the optimal (Utopia) solution.

Figure 4d: MNLMPC for model 1 u1 vs t.

Figure 4e: MNLMPC for model 1 u2 vs t.

Figure 4f: MNLMPC for model 1 u1 (Savitzky Golay) vs t.

Figure 4g: MNLMPC for model 1 u2 (Savitzky Golay) vs t).

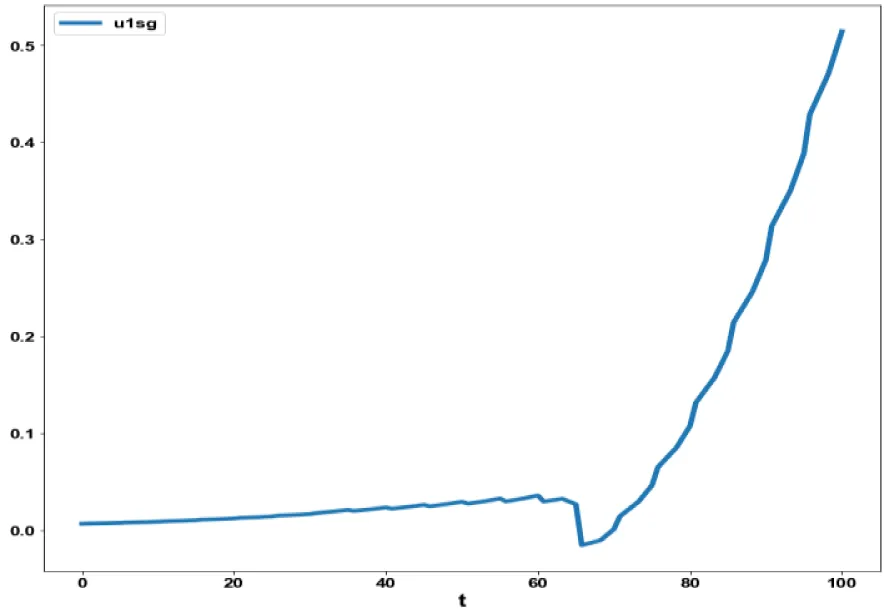
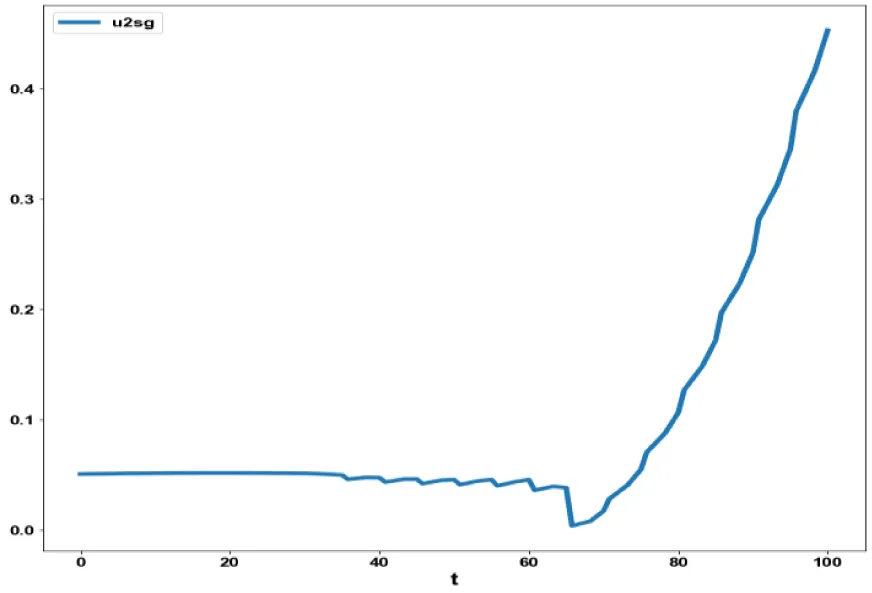
For the MNLMPC calculations involving model 2, ${\displaystyle \sum _{t_{i=0}}^{t_i=t_f}ival(t_i)}$ was minimized ${\displaystyle \sum _{t_{i=0}}^{t_i=t_f}wval(t_i)}$ was maximized individually and resulted in values of 0 and 200. The overall optimal control problem will involve the minimization of

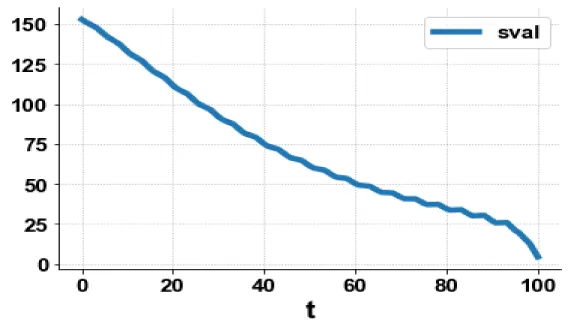
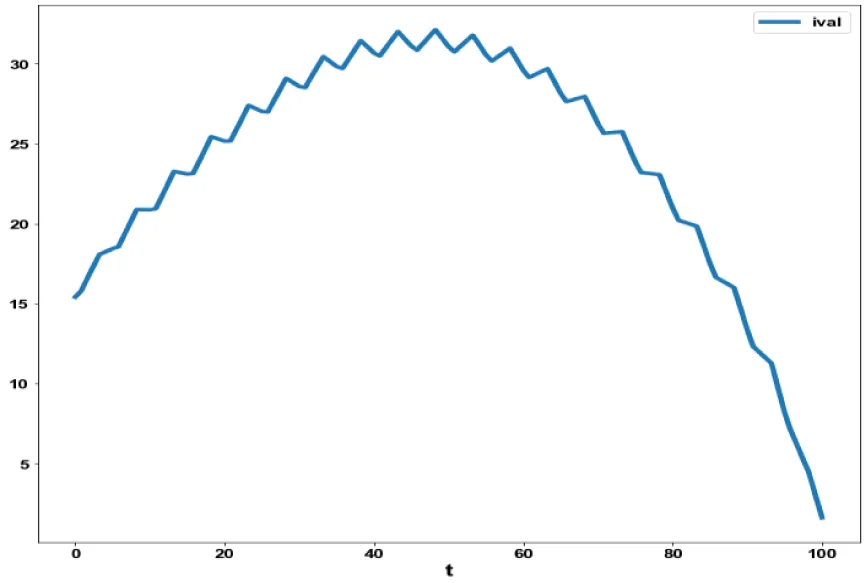
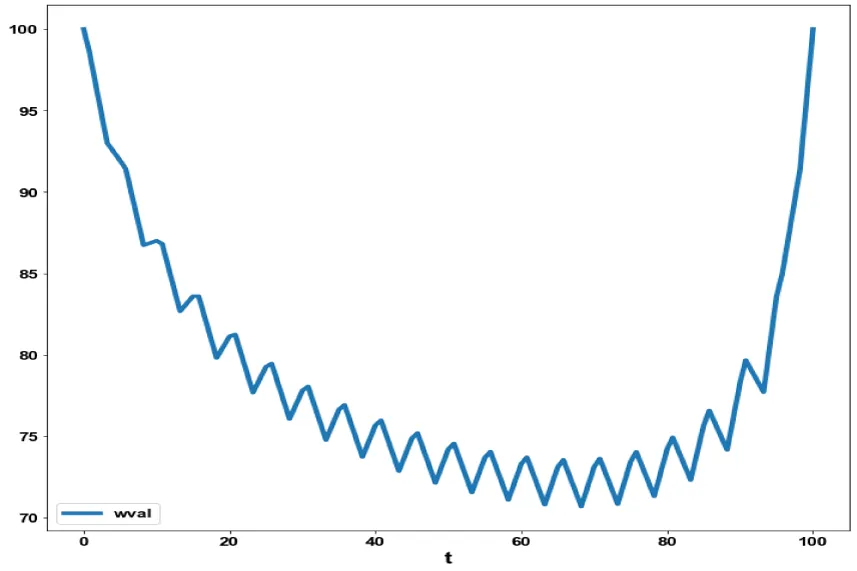
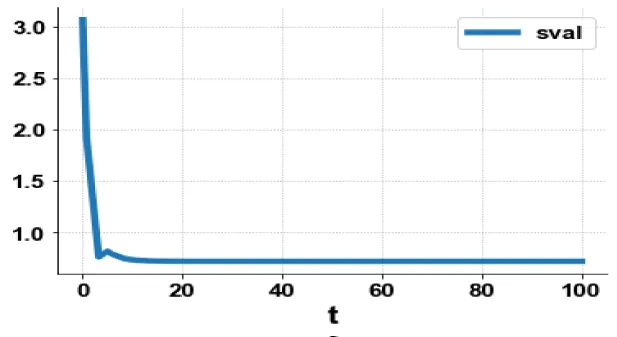
${({\displaystyle \sum _{t_{i=0}}^{t_i=t_f}ival(t_i)}-0)}^2+{({\displaystyle \sum _{t_{i=0}}^{t_i=t_f}wval(t_i)}-200)}^2$ was minimized subject to the equations governing the model. This led to a value of zero (the Utopia solution. The various concentration profiles for this MNLMPC calculation are shown in figures 5a-c. (Figures 5a-c) indicate the variation sval, ival, wval versus time.

Figure 5a: MNLMPC model 2, sval vs t.

Figure 5b: MNLMPC model 2, ival vs t.

Figure 5c: MNLMPC model 2, wval s t.

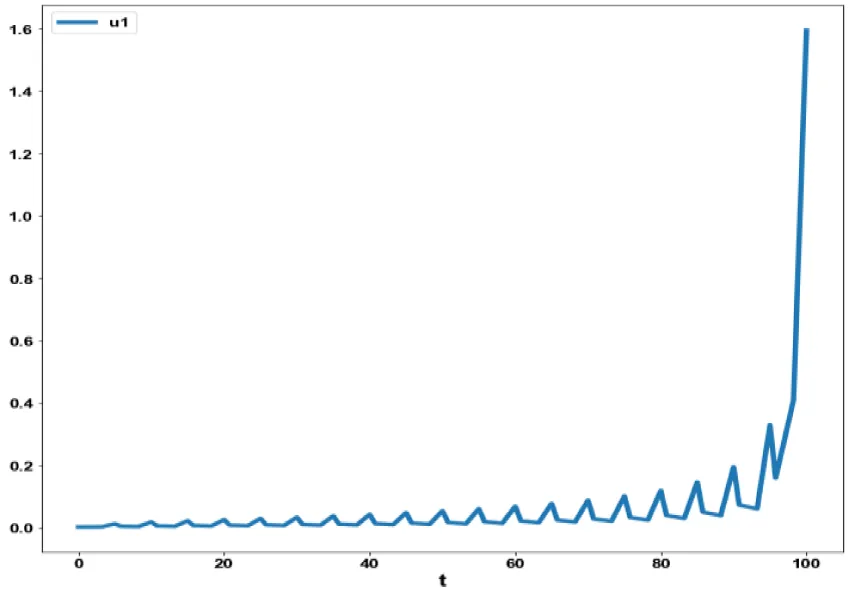
The obtained control profile of u1 and u2 exhibited noise (Figures 5d, e). This issue was addressed using the Savitzky-Golay Filter. The smoothed version of this profile is shown in figures 4f, g. The MNLMPC control values obtained for u1 and u2 are 0.002779 and 0.02749. The MNLMPC calculations converged to the Utopia solution, validating the analysis by Sridhar LN. [39], which demonstrated that the presence of a limit point/branch point enables the MNLMPC calculations to reach the optimal (Utopia) solution.

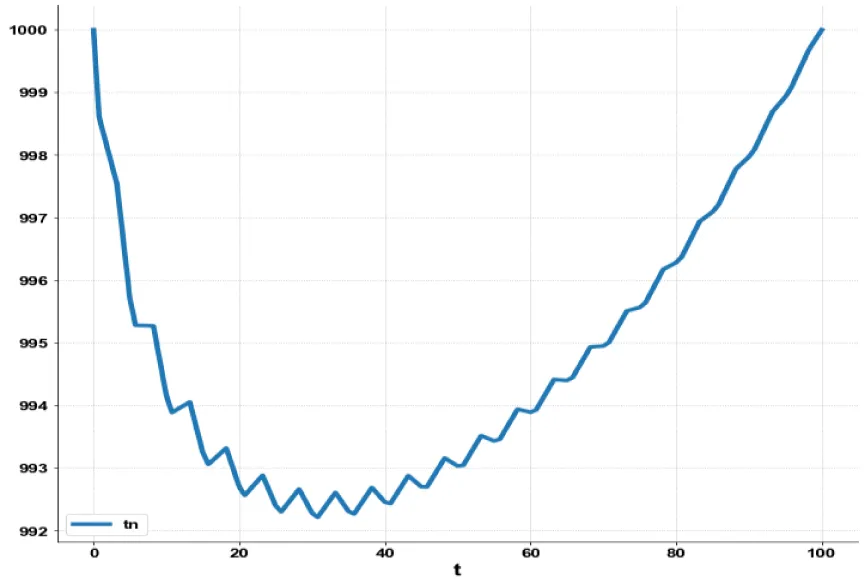
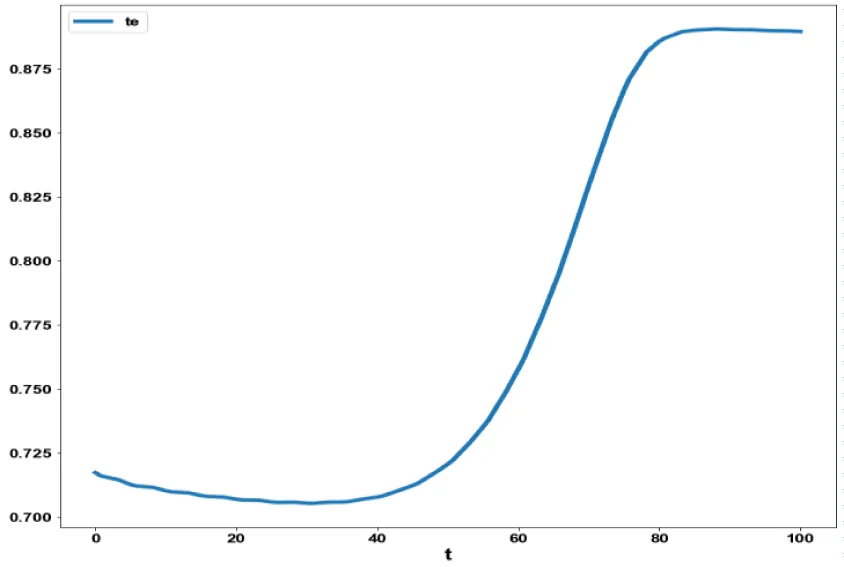
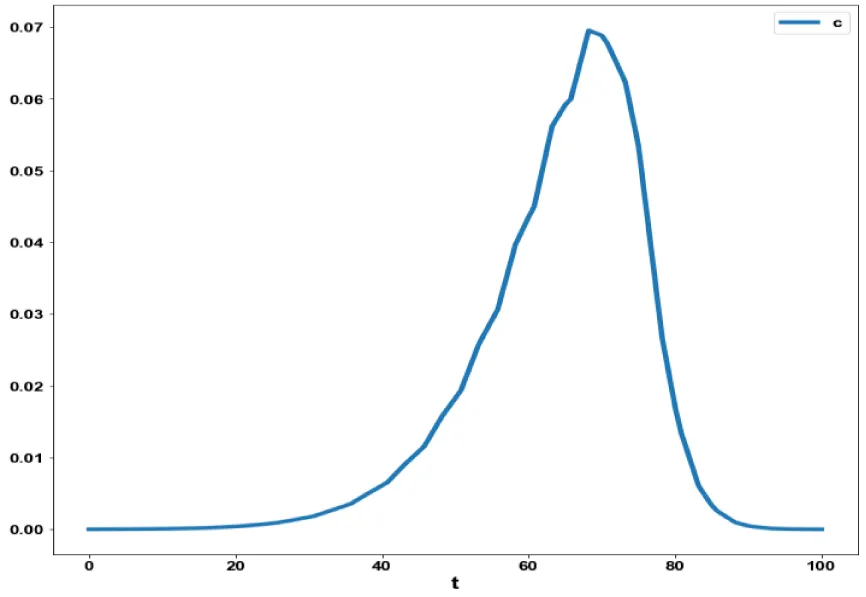
For the MNLMPC calculations involving model 3, ${\displaystyle \sum _{t_{i=0}}^{t_i=t_f}lval(t_i)}$ was minimized ${\displaystyle \sum _{t_{i=0}}^{t_i=t_f}aval(t_i)}$ was maximized individually and resulted in values of 0 and 5.47269. The overall optimal control problem will involve the minimization of ${({\displaystyle \sum _{t_{i=0}}^{t_i=t_f}lval(t_i)}-0)}^2+{({\displaystyle \sum _{t_{i=0}}^{t_i=t_f}aval(t_i)}-5.47269)}^2$ was minimized subject to the equations governing the model. This led to a value of zero (the Utopia solution. The MNLMPC control values obtained for u was 0.6345. The various concentration profiles for this MNLMPC calculation are shown in figures 6a-6f. (Figures 6a-e) show the variation of sval, aval, dval, lval, tval with respect to time while fig 6f shows the variation of the control variable. The MNLMPC calculations converged to the Utopia solution, validating the analysis by Sridhar LN. [39], which demonstrated that the presence of a limit point/branch point enables the MNLMPC calculations to reach the optimal (Utopia) solution.

Figure 5d: MNLMPC model 2, sval vs t.

Figure 5e: MNLMPC model 2, u2 vs t.

Figure 5f: MNLMPC model 2, u1 (Savitzky Golay) vs t.

Figure 5g: MNLMPC model 2, u2 (Savitzky Golay) vs t.

Figure 6a: MNLMPC model 3, sval vs t.

Figure 6b: MNLMPC model 3, aval vs t.

Figure 6c: MNLMPC model 3, tval vs t.

Figure 6d: MNLMPC model 3, lval vs t.

Figure 6e: MNLMPC model 3, dval vs t.

Figure 6f: MNLMPC model 3, u vs t.

Model 1 and Model 3 displayed limit points, while Model 2 demonstrated a branch point. In all three instances, the MNLMPC calculations converged to the Utopia solution, validating the analysis of Sridhar LN. [39] which showed that the existence of a limit point or a branch point allows the MNLMPC calculations to achieve the best possible (Utopia) solution.

Bifurcation analysis and Multiobjective nonlinear model predictive control calculations were performed on three leukemia models. The bifurcation analysis revealed the existence of limit and branch points. The limit and branch points (which cause multiple steady-state solutions from a singular point) are very beneficial as they enable the Multiobjective nonlinear model predictive control calculations to converge to the Utopia point (The best possible solution) in both models. A combination of bifurcation analysis and multiobjective nonlinear model predictive control for leukemia disease models is the main contribution of this paper.

All data used is presented in the paper.

The author, Dr. Lakshmi N Sridhar has no conflict of interest.

Dr. Sridhar thanks Dr. Carlos Ramirez and Dr. Suleiman for encouraging him to write single-author papers.

1. Deininger MW, Goldman JM, Melo JV. The molecular biology of chronic myeloid leukemia. Blood. 2000 Nov 15;96(10):3343-56. PMID: 11071626.
2. Topaly J, Zeller WJ, Fruehauf S. Synergistic activity of the new ABL-specific tyrosine kinase inhibitor STI571 and chemotherapeutic drugs on BCR-ABL-positive chronic myelogenous leukemia cells. Leukemia. 2001 Mar;15(3):342-7. doi: 10.1038/sj.leu.2402041. PMID: 11237055.
3. Deininger MW, Druker BJ. Specific targeted therapy of chronic myelogenous leukemia with imatinib. Pharmacol Rev. 2003 Sep;55(3):401-23. doi: 10.1124/pr.55.3.4. Epub 2003 Jul 17. PMID: 12869662.
4. Deininger MW, O'Brien SG, Ford JM, Druker BJ. Practical management of patients with chronic myeloid leukemia receiving imatinib. J Clin Oncol. 2003 Apr 15;21(8):1637-47. doi: 10.1200/JCO.2003.11.143. Epub 2003 Mar 13. PMID: 12668652.
5. Goldman JM, Melo JV. Chronic myeloid leukemia--advances in biology and new approaches to treatment. N Engl J Med. 2003 Oct 9;349(15):1451-64. doi: 10.1056/NEJMra020777. PMID: 14534339.
6. Pujo-Menjouet L, Mackey MC. Contribution to the study of periodic chronic myelogenous leukemia. C R Biol. 2004 Mar;327(3):235-44. doi: 10.1016/j.crvi.2003.05.004. PMID: 15127894.
7. Baccarani M, Martinelli G, Rosti G, Trabacchi E, Testoni N, Bassi S, Amabile M, Soverini S, Castagnetti F, Cilloni D, Izzo B, de Vivo A, Messa E, Bonifazi F, Poerio A, Luatti S, Giugliano E, Alberti D, Fincato G, Russo D, Pane F, Saglio G; GIMEMA Working Party on Chronic Myeloid Leukemia. Imatinib and pegylated human recombinant interferon-alpha2b in early chronic-phase chronic myeloid leukemia. Blood. 2004 Dec 15;104(13):4245-51. doi: 10.1182/blood-2004-03-0826. Epub 2004 Aug 19. PMID: 15319292.
8. Moore H, Li NK. A mathematical model for chronic myelogenous leukemia (CML) and T cell interaction. J Theor Biol. 2004 Apr 21;227(4):513-23. doi: 10.1016/j.jtbi.2003.11.024. PMID: 15038986.
9. Adimy M, Crauste F, Ruan S. A mathematical study of the haematopoiesis process with applications to chronic myelogenous leukemia, SIAM J. Appl. Math. 2005;65(4):1328. doi: 10.1137/040604698.
10. Michor F, Hughes TP, Iwasa Y, Branford S, Shah NP, Sawyers CL, Nowak MA. Dynamics of chronic myeloid leukaemia. Nature. 2005 Jun 30;435(7046):1267-70. doi: 10.1038/nature03669. PMID: 15988530.
11. Nanda S, Moore H, Lenhart S. Optimal control of treatment in a mathematical model of chronic myelogenous leukemia. Math Biosci. 2007 Nov;210(1):143-56. doi: 10.1016/j.mbs.2007.05.003. Epub 2007 May 18. PMID: 17599363.
12. Liso A, Castiglione F, Cappuccio A, Stracci F, Schlenk RF, Amadori S, Thiede C, Schnittger S, Valk PJ, Döhner K, Martelli MF, Schaich M, Krauter J, Ganser A, Martelli MP, Bolli N, Löwenberg B, Haferlach T, Ehninger G, Mandelli F, Döhner H, Michor F, Falini B. A one-mutation mathematical model can explain the age incidence of acute myeloid leukemia with mutated nucleophosmin (NPM1). Haematologica. 2008 Aug;93(8):1219-26. doi: 10.3324/haematol.13209. Epub 2008 Jul 4. PMID: 18603563.
13. Ommen HB, Nyvold CG, Braendstrup K, Andersen BL, Ommen IB, Hasle H, Hokland P, Ostergaard M. Relapse prediction in acute myeloid leukaemia patients in complete remission using WT1 as a molecular marker: development of a mathematical model to predict time from molecular to clinical relapse and define optimal sampling intervals. Br J Haematol. 2008 Jun;141(6):782-91. doi: 10.1111/j.1365-2141.2008.07132.x. Epub 2008 Apr 10. PMID: 18410450.
14. Cucuianu A, Precup R. 2010. A hypothetical-mathematical model of acute myeloid leukaemia pathogenesis. Comput Math Methods Med. 2010;11(1):49-65. doi: 10.1080/17486700902973751.
15. Döhner H, Estey EH, Amadori S, Appelbaum FR, Büchner T, Burnett AK, Dombret H, Fenaux P, Grimwade D, Larson RA, Lo-Coco F, Naoe T, Niederwieser D, Ossenkoppele GJ, Sanz MA, Sierra J, Tallman MS, Löwenberg B, Bloomfield CD; European LeukemiaNet. Diagnosis and management of acute myeloid leukemia in adults: recommendations from an international expert panel, on behalf of the European LeukemiaNet. Blood. 2010 Jan 21;115(3):453-74. doi: 10.1182/blood-2009-07-235358. Epub 2009 Oct 30. PMID: 19880497.
16. Komarova NL. Mathematical modeling of cyclic treatments of chronic myeloid leukemia. Math Biosci Eng. 2011 Apr;8(2):289-306. doi: 10.3934/mbe.2011.8.289. PMID: 21631131.
17. Stiehl T, Czochra AM. Mathematical modeling of leukemogenesis and cancer stem cell dynamics. Math. Model Nat Phenom. 2012;7(1):66-202. doi: 10.1051/mmnp/20127199.
18. MacLean AL, Lo Celso C, Stumpf MP. Population dynamics of normal and leukaemia stem cells in the haematopoietic stem cell niche show distinct regimes where leukaemia will be controlled. J R Soc Interface. 2013 Jan 24;10(81):20120968. doi: 10.1098/rsif.2012.0968. PMID: 23349436; PMCID: PMC3627104.
19. MacLean AL, Filippi S, Stumpf MP. The ecology in the hematopoietic stem cell niche determines the clinical outcome in chronic myeloid leukemia. Proc Natl Acad Sci U S A. 2014 Mar 11;111(10):3883-8. doi: 10.1073/pnas.1317072111. Epub 2014 Feb 24. PMID: 24567385; PMCID: PMC3956166.
20. Agarwal M, Bhadauria AS. Mathematical modeling and analysis leukemia: Effect of external T cells infusion. Appl Appl Math Int J. 2015;10(1):249-266.
21. Clapp G, Levy D. A Review of Mathematical Models for Leukemia and Lymphoma. Drug Discov Today Dis Models. 2015 Summer;16:1-6. doi: 10.1016/j.ddmod.2014.10.002. Epub 2014 Nov 29. PMID: 26744598; PMCID: PMC4698906.
22. Crowell HL, MacLean AL, Stumpf MP. Feedback mechanisms control coexistence in a stem cell model of acute myeloid leukaemia. J Theor Biol. 2016 Jul 21;401:43-53. doi: 10.1016/j.jtbi.2016.04.002. Epub 2016 Apr 27. PMID: 27130539; PMCID: PMC4880151.
23. Austin R, Smyth MJ, Lane SW. Harnessing the immune system in acute myeloid leukaemia. Crit Rev Oncol Hematol. 2016 Jul;103:62-77. doi: 10.1016/j.critrevonc.2016.04.020. Epub 2016 May 11. PMID: 27247119.
24. Zeidan AM, Mahmoud D, Kucmin-Bemelmans IT, Alleman CJ, Hensen M, Skikne B, Smith BD. Economic burden associated with acute myeloid leukemia treatment. Expert Rev Hematol. 2016 Jan;9(1):79-89. doi: 10.1586/17474086.2016.1112735. Epub 2015 Nov 14. PMID: 26568358.
25. Masarova L, Kantarjian H, Garcia-Mannero G, Ravandi F, Sharma P, Daver N. Harnessing the Immune System Against Leukemia: Monoclonal Antibodies and Checkpoint Strategies for AML. Adv Exp Med Biol. 2017;995:73-95. doi: 10.1007/978-3-319-53156-4_4. PMID: 28321813.
26. Lichtenegger FS, Krupka C, Haubner S, Köhnke T, Subklewe M. Recent developments in immunotherapy of acute myeloid leukemia. J Hematol Oncol. 2017 Jul 25;10(1):142. doi: 10.1186/s13045-017-0505-0. PMID: 28743264; PMCID: PMC5526264.
27. Krupar R, Schreiber C, Offermann A, Lengerke C, Sikora AG, Thorns C, Perner S. In silico analysis of anti-leukemia immune response and immune evasion in acute myeloid leukemia. Leuk Lymphoma. 2018 Oct;59(10):2493-2496. doi: 10.1080/10428194.2018.1434883. Epub 2018 Feb 12. PMID: 29431550.
28. Sharp JA, Browning AP, Mapder T, Burrage K, Simpson MJ. Optimal control of acute myeloid leukaemia. J Theor Biol. 2019 Jun 7;470:30-42. doi: 10.1016/j.jtbi.2019.03.006. Epub 2019 Mar 8. PMID: 30853393.
29. Khatun MS, Biswas MHA. Mathematical analysis and optimal control applied to the treatment of leukemia. J Appl Math Comput. 2020;64:331-353. doi: 10.1007/s12190-020-01357-0.
30. Dhooge A, Govearts W, Kuznetsov AY. A Matlab package for numerical bifurcation analysis of ODEs. ACMTransactions on Mathematical Software. 2003;29(2):141-164. doi: 10.1145/779359.77936.
31. Dhooge AW, Govaerts Y, Kuznetsov A, Mestrom W, Riet AM. CL_MATCONT; A continuation toolbox in Matlab. 2004;161-166. doi: 10.1145/952532.952567.
32. Kuznetsov YA. Elements of applied bifurcation theory. NY:Springer;1998. 
33. Kuznetsov YA. Five lectures on numerical bifurcation analysis. Utrecht University. NL: 2009.
34. Govaerts WJF. Numerical methods for bifurcations of dynamical equilibria. Siam. 2000.
35. Flores-Tlacuahuac A.   Pilar morales and martin riveral Toledo. Multiobjective nonlinear model predictive control of a class of chemical reactors. I & EC research. 2012;51(17):5891-5899.
36. Hart, William E, Carl D. Laird, Jean-Paul Watson, David L. Woodruff, Gabriel A. Hackebeil, Bethany L. Nicholson, John D. Siirola. Pyomo – Optimization modeling in python. 3rd ed; 2017.
37. Wächter A, Biegler L. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math Program. 2006;106:25-57. doi: 10.1007/s10107-004-0559-y.
38. Tawarmalani M, Sahinidis NV. A polyhedral branch-and-cut approach to global optimization.  Mathematical Programming. 2005;103(2):225-249. doi: 10.1007/s10107-005-0581-8.
39. Sridhar LN. Coupling bifurcation analysis and multiobjective nonlinear model predictive control. Austin Chem Eng. 2024;10(3):1107.
40. Upreti SR. Optimal control for chemical engineers. Taylor and Francis. 2013.