Investigation of Mechanical Thermodiffusion Processes Under Influence of Microwave Irradiation

In this mini-report, the interrelated processes of heat and mass transfer, which take into account the nature of interphase interaction in moistened porous media, are examined. A closed system of balance diffusion equations for the liquid phase and components of the gas mixture of water vapor and dry air is reviewed. The energy or heat balance equation, which contains the intensity of sources of evaporation or condensation during the phase transformation of liquid into water vapor, is analyzed. The phenomenon of dielectric relaxation into a heterogeneous porous layer under the influence of a symmetric electromagnetic field of microwave frequency is modeled by an isotropic (non-magnetic) dielectric with weak or insignificant conductivity and strongly depends on pore saturation by liquid. With the help of the spatial averaging method, taking into account the interphase interaction, the equations for mechanical balance are proposed, in which the exchange integrals of the moment of impulse and mechanical forces are applied. The macroscopic equations of mechanical balance into the solid and liquid phases are proposed, from where the analytical expressions for effective thermal and moisture stresses in the porous wetted layer are obtained using the accepted approximations and taking into account the known relations for stresses in the solid and liquid phases. According to the results of the heat and mass process numerical simulation, the distribution of thermal and moisture stress is obtained.

Microwave technologies are widely used in industrial processes, such as drying (textiles, wood, paper and ceramics), heat treatment of metals (hardening), disposal (recycling or disposal) of radioactive waste. In medicine, they are used to restoring frozen tissues, warm blood, and treat tumours. The greatest consumer interest in microwave technologies arises in the food preparation industry, namely the processes of baking, pasteurization, dehydration and sterilization. Volumetric heating of the material by microwave irradiation (internal dielectric heating) refers to accelerated methods of heat exchange and removal of moisture from the material. For various methods of dielectric heating, the prediction (forecasting) of heat and mass transfer (transport) processes is extremely important in terms of equipment development, optimization processes, and product quality improvement. Direct experimental measurement of temperature and moisture content in porous material is a complex and troublesome process. Therefore, a significant amount of scientific research was carried out to model the transport (diffusion) processes of heat and mass transfer for such heterogeneous materials. Several different techniques or methods of numerical calculations, which are based on the use of the finite difference method [1,2], finite elements [3] or the line transfer matrix method [4] have been used to simulate microwave heating with varying degrees of success. In fact, when performing these calculations, it is necessary to know [5-10] the constant dielectric or thermal properties of the material.

A lot of research has been done in the modelling of microwave heating of materials [11], but we have little progress in modelling the transfer of heat and mass during microwave drying. Since under influence of dielectric heating or drying in an electromagnetic field, the material with dielectric loss of power from microwave irradiation has no permanent electro-physical properties, for most materials the dielectric properties change as a function of moisture content and temperature. Therefore, during microwave heating (drying), the distribution of the electromagnetic field in the body (material) is strongly related to the processes of heat and mass transfer. Changes in the local moisture content and temperature affect the dielectric properties of the material, including the distribution of the electromagnetic field. The size of the load (material) relative to the waveguide or the drying cavity, the effect of the wave resistance (impedance) of the cavity, the amount of radiation power that is reflected from the inner walls of the cavity (resonator) in the direction of the on magnetron determine the quality of the microwave equipment.

Since the detailed distribution of the power of the electromagnetic field (internal heat sources) within the material loading is quite difficult to model [4], most studies assume that the lines of force of the electromagnetic field during microwave irradiation on the surface of the material are uniform and normal to the surface. It is also assumed that the power of the external irradiation in the body decays in accordance [12] with the exponential law. Such approach was happy and applied to modelling of heat and mass transport of dielectric the heated product of food [13,14]. A simple reflection was expressed according to investigation [15], where heat sources under dielectric losses of microwave irradiation in the range of solid product is assumed uniform. In reality, into the mentioned theoretical works the understanding of drying processes is limited, because under description of humidity transfer in porous media at isothermal conditions is used in general. For more developed models a law of molecular diffusion [16] is applied and assumed [17,18], that heat gradient is the main division force into processes of mass transport or transfer. It's need to pointed, that results of numerical modelling according to mentioned above models for humidity diffusion as rule do not agree with experimental measured [19] in the more cases.

Same researcher development of the models [20] into approach, when diffusion of water vapour is main mechanism of humidity transport during of drying processes. For too refined methods for describing of drying (microwave heating) the two area transport models [21-23] are treated. In these models is assumed, that two different area (region) for describing of humidity transport during drying (wetted and dried area) is existed. In the wetted area, moisture content is great as maximal sorption value for water vapour and basic mechanism for transport (transfer) of humidity is movement of liquid. In sorption region the movement of adsorbed (bounded) water and water vapour is the basic reason of mass transport. The applying of this model is limited, because during the long (limited) process of drying the division (boundary) between wetted and sorption areas (regions) is conventional.

A reference review is shown [24] that main progress was made into development of transport (diffusion) models under investigation of physics of ground, where main interest was concentrated on the utilization of nuclear remains and management of water resources. The basic formulation was development for interconnected processes of heat and mass transfer into works [25-27]. The main approaches are based on assumption that general transport potential consist on the two components: temperature and capillary potential.

During microwave drying, an induces by microwave (thermal) heating increment in density of water vapour and humidity potential is calling of movement of humidity from more heated into cooled area. A general restriction or deficiency of mentioned isothermal models is absence of the thermal induced changing of humidity. Firstly, this is due to a significant difference in the distribution of moisture in the porous material, which is caused by the processes of evaporation or condensation.

In fact, in the context of drying processes, reformulation of the problem in terms of moisture content and temperature is desirable for a fundamental understanding of drying processes, especially when modelling diffusion (transport) processes under conditions of intense internal microwave heating. Foremost, this is due to a significant difference in the distribution of moisture in the porous material, which is caused by the processes of evaporation or condensation.

The nature of stresses in porous materials that arise during microwave heating, as a result of changes in temperature and moisture distribution, also remains insufficiently researched. For example, despite the fact that the hydrothermal behavior of concrete under thermal (radiation) heating is described in detail in the work [28], the author is aware of only one scientific work [29], where the maximum values of thermal stresses caused by internal microwave heat sources were calculated in the specified material. Some attempts at computer simulation of the stressed state of the specified material under microwave irradiation were carried out in works [30,31], where only the energy (thermal) balance equation was used to calculate the thermal and elastic properties of the material.

Special attention should be paid to the study [32-36] of the properties of thermal and moisture stresses during microwave irradiation under conditions of phase transformation (evaporation or condensation) and changes in the pressure of the gas medium into the pores of the moistened material. Theoretical models for describing the dependence of microwave heating sources on the distribution of moisture and temperature in a porous medium also need improvement and development [37], especially in view of modelling effective (measured) characteristics due to the corresponding properties of phases or components in the studied wetted porous sample.

This porous sample or area is well described into the work [38], from there are follows that by using the local averaging method [39] the inhomogeneous body can be described through the appropriate continuous locals into space of coordinate and times the physical quantities. It is giving the possibility to review porous sample as the superposition of three continuous materials: skeletons (S), liquids (L), and gas (G). Under such an approach, the equations of the physical model into porous media can be rewritten relatively to the defined [39] by the homogenization method the averaged quantities. Such equations are formally equivalent to the equations for the homogeneous (isotropic) one phase media according to the approach of the solid or continuous media.

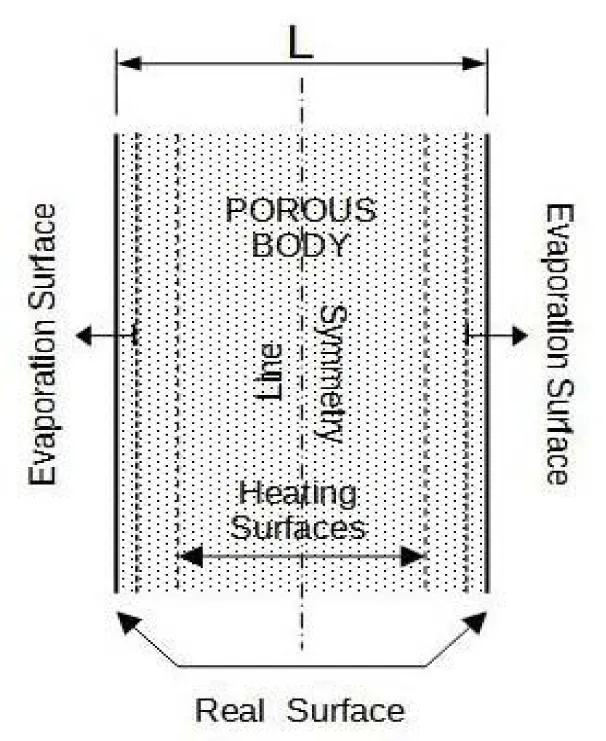
Let's define the object of studies. This is the one-dimensional porous wetted plate length of L (Figure 1) which is under the influence of symmetrical microwave irradiation of the fixed power. The constant convective flow by the hot air at the surfaces of the plate is also additionally applied during all times of microwave treatment, so in general it can be classified as the mixed microwave-convective treatment of porous wetted or humidified samples.

We are modeling such drying systems mathematically via the introduction of dynamical boundary conditions. There is confirmed by other authors [40,41] that, conditionally, it is possible to highlight the two zones during microwave treatment for a porous sample: the wetted and heated zones. The term zones will mean a one-dimensional area from the internal surface to the real hard boundaries of the body into the direction of the external environment. The moving zones are interconnected due to the dependence of diffusion coefficients in the internal volume of the sample from humidity, as well as the time dependences of surface heat and mass transfer coefficients on the real physical boundaries of the mentioned porous sample.

The thicknesses of the near-surface zones relatively to the surface of symmetry $S_0$ (Figure 1) can be described by the corresponding lengths.

$\Delta h_1=\frac{1}{h_m}{\psi }_G\frac{p_{\nu }}{x_{\nu }}{|}_{S_0}\text{ and }\Delta h_2=\frac{1}{h_T}{\lambda }_{eff}{|}_{S_0}\text{ (1)}$

where ${\psi }_G=\left[k_{in}{k}_{rG}\right]/{\mu }_G$ [42], here $k_{in}$ and $k_{\text{rG}}$ are the intrinsic permeability of skeleton and liquid phase, ${\mu }_G$ is the gas dynamical viscosity, $h_m$ and $h_T$ are the constant surface mass and heat exchange coefficients under convective heating conditions and , as it was mentioned below, is the surface of symmetry of the porous plate.

Mechanical properties For a spatially isotropic homogeneous solid phase (framework or skeleton) in a porous medium under the condition of the absence of external force loading, the quasi-static problem of linear thermoelastic [43-45] is formulated in the form of relations

$\begin{array}{l}{\widehat{T}}_{\alpha \beta ,\beta }+\widehat{I}{F}_{\alpha }=0,\\ F_{\alpha }=-\phi \left[\frac{\partial P_G}{\partial x_{\alpha }}-{\eta }_L\frac{\partial P_C}{\partial x_{\alpha }}\right]+\phi P_C\frac{\partial {\eta }_L}{\partial x_{\alpha }}\end{array}$

where ${\hat{T}}^{*}=\left(1-\phi \right)\left({\hat{t}}_S^{\text{'}}-K{\alpha }_S^T\left(T-T_0\right)\hat{I}\right)$ is the leading stress tensor ( here ${\hat{t}}_S^{\text{'}}$ is the own tension of porous skeleton [46], $K$ and ${\alpha }_S^T$ are the averaged lateral compression modulus and thermal expansion coefficient of the porous skeleton correspondingly [47]) $F_{\alpha }$ , is the components of internal (pondermotore) forces due to gas pressure, $P_G$ capillary pressure $P_C$ and liquid pore saturation ${\eta }_L$ [39] at the averaged constant porosity of the body $\phi$ , $T_0$ is the initial equilibrium temperature and $\hat{I}$ is the diagonal tensor.

In the case of a one-dimensional porous plate (Figure 1), which is under the influence of symmetrical external microwave irradiation according to the conditions of compatibility of Saint-Venant deformations [48], the system of equations for the stress component of the tensor takes the form

$\frac{{\partial }^2{T}_{xx}^{*}}{\partial x^2}+\frac{\partial F}{\partial x}=0$

$\begin{array}{l}\frac{{\partial }^2{T}_{yy}^{*}}{\partial x^2}+\frac{1}{1-\nu }\left(E\frac{{\partial }^{2}L}{\partial x^2}+\nu \frac{\partial F}{\partial x}\right)=\\ 0, \frac{{\partial }^2{T}_{zz}^{*}}{\partial x^2}+\frac{1}{1-\nu }\left(E\frac{{\partial }^{2}L}{\partial x^2}+\nu \frac{\partial F}{\partial x}\right)=0\end{array}$

here $E$ and $\nu$ are the averaged Young[48] module and Poisson [48] ratio.

Force loads into the internal area of the plate are also determined

$\begin{array}{l}{\Phi }^{*}\left(x\right)=-\underset{0}{\overset{x}{{\displaystyle \int }}}F\left(x\right)dx=\\ -\left[\Phi \left(x\right)-\Phi \left(0\right)\right], L^{*}\left(x\right)=L\left(x\right)-L\left(0\right)\text{ (2)}\end{array}$

where

$\Phi \left(x\right)=-{{\displaystyle \int }}^{\text{}}F\left(x\right)dx=\phi \left[P_G-{\eta }_L{P}_C\right],$

$L\left(x\right)\equiv -\left(1-\phi \right)K{\alpha }_S^T\left(T-T_0\right)$

are the quantity of humidity and thermal stress and $\Phi \left(0\right)L\left(0\right)$ are corresponding constant values on the internal surface of symmetry (Figure 1 is the surface $S_0$ at $x=0$ ) for the linear porous plate .

According to the symmetry conditions, the boundary conditions for a plate of finite $L$ thickness are applied: 1. There are no internal forces ${\Phi }^{*}\left(0\right)=L^{*}\left(0\right)=0$ along the plane of symmetry of the plate; 2. The boundary surfaces of the plate are free from the external loads $\underset{-L/2}{\overset{L/2}{{\displaystyle \int }}}{T}_{xx}^{*}dx=\underset{-L/2}{\overset{L/2}{{\displaystyle \int }}}{T}_{yy}^{*}dx=\underset{-L/2}{\overset{L/2}{{\displaystyle \int }}}{T}_{zz}^{*}dx=0$ ; 3. The derivative of stresses along the plane of symmetry $\frac{\partial T_{xx}^{*}\left(0\right)}{\partial x}=\frac{\partial T_{yy}^{*}\left(0\right)}{\partial x}=\frac{\partial T_{zz}^{*}\left(0\right)}{\partial x}=0$ is equal to zero.

Then the solution of the equations of the quasi-linear thermoelastic problem under the action of internal (moisture and thermal) loads has the form of the stresses

$T_{xx}^{*}={\Phi }^{*}\left(x\right)-{\Phi }^{*}\left(x\right)$

$T_{yy}^{*}\left(x\right)=T_{zz}^{*}\left(x\right)=\frac{E}{1-\nu }\left[M^{*}\left(x\right)-M^{*}\left(x\right)\right]$

and the deformation

$\begin{array}{c}\begin{array}{l}{E}_{yy}^{*}\left(x\right)=E_{zz}^{*}\left(x\right)=\\ \frac{1}{E}\left[\left(1-\nu \right)T_{yy}^{*}\left(x\right)-\nu T_{xx}^{*}\left(x\right)\right]+L\left(x\right)-L\left(0\right),\end{array}\\ E_{xx}^{*}=\frac{1}{E}\left[T_{zz}^{*}-2\nu T_{yy}^{*}\right]+L\left(x\right)-L\left(0\right),\end{array}$

Correspondingly, where

$M^{*}\left(x\right)=L^{*}\left(x\right)-\frac{\nu }{E}{\Phi }^{*}\left(x\right)$ is an expression for the total internal forces, and $M^{*}=\frac{1}{L}\underset{-L/2}{\overset{L/2}{{\displaystyle \int }}}{M}^{*}\left(x\right)dx$ or ${\Phi }^{*}=\frac{1}{L}\underset{-L/2}{\overset{L/2}{{\displaystyle \int }}}{\Phi }^{*}\left(x\right)dx$ refers to the averaged effort values.

General equations Using the well-known [49,50] approaches for describing heat and mass transfer during microwave heating, we obtain a system of closed equations for the heat and moisture diffusion

$\begin{array}{l}{(}_{\rho }{\partial }_{t}T(x,t)-\frac{1}{2}r{\partial }_t\left[c_L{}^L-{\partial }_t{c}_{\nu }{}^G\right]=\\ {\partial }_x\left[{\lambda }_{eff}{\partial }_{x}T\left(x,t\right)\right]+\end{array}$

$+\frac{1}{2}r\overrightarrow{\nabla }\cdot \left[J_L^x-J_{\nu }^x\right]+{\stackrel{\cdot }{q}}^t(x)\text{ (3)}$

${\partial }_t{c}_L{}^G+{\partial }_x{\overrightarrow{J}}_L=\stackrel{\cdot }{I } {\partial }_t{c}_{\nu }{}^G+{\partial }_x{\overrightarrow{J}}_{\nu }=-\stackrel{\cdot }{I}$

${\partial }_t{c}_a{}^G=-{\partial }_x{J}_a^x$

here ${\left(\rho C_p\right)}_{eff}={\displaystyle \sum }_{\sigma }{\theta }_{\sigma }{\rho }_{\sigma }{}^{\sigma }{C}_p^{\sigma }$ and ${\lambda }_{eff}={\displaystyle \sum }_{\sigma }{\theta }_{\sigma }{\lambda }_{\sigma }{}^{\sigma }$ (where $\sigma =\left\{S,L,G\right\}$ is the index of phase) are the effective thermal characteristics of the porous material, $T$ is the thermodynamic temperature, $\dot{q}$ and $\dot{I}$ are the heat and mass surfaces intensity correspondingly $C_p^{\sigma }$ , and ${\lambda }_{\sigma }{}^{\sigma }$ are the specific capacity and thermal conduction of $\sigma$ -phase and $r$ is the latent heat of vaporization.

With the proposed by the author of this review boundary conditions, the solutions of such a system of partial differential equations can be found according to the obtained analytical expression [51] for the heat sources

$\begin{array}{c}{\stackrel{.}{q}}^t\left(x\right)=2P_{in}\left|{\overline{n}}_{\omega }\left(t\right)\right|{\left|T\left(t\right)\right|}^2\alpha \left(x,t\right)\sqrt{\frac{1}{2}\left(1+\frac{1}{\sqrt{1+t{g}^2{\delta }_{\omega }\left(x,t\right)}}\right)}\times \\ \times \left(Exp\left[-2\underset{-L/2}{\overset{x}{{\displaystyle \int }}}\alpha \left(x,t\right)dx\right]+Exp\left[-2\underset{x}{\overset{L/2}{{\displaystyle \int }}}\alpha \left(x,t\right)dx\right]\right)\end{array}$

Then we can determine the stress-strain state of the linear body, with the values calculated relatively to the plane of symmetry

$\Phi \left(x\right)=-{{\displaystyle \int }}^{\text{}}F\left(x\right)dx=\phi \left[P_G\left(x,t\right)-{\eta }_L{P}_C\left(x,t\right)\right], \text{ (4)}$

$L\left(x\right)=-\left(1-\phi \right)K{\alpha }_S^T\left[T\left(x,t\right)-T_0\right]$

With defined above humidity and thermal internal forces loadings.

The closed system of equations is received by performing the conditions of compatibility, which take into account the weak variability of volume (phase) and dielectric (wave) properties of the three-phaseporous humidified media

$\frac{1}{{\theta }_{\sigma }\left(x,t\right)}\frac{\partial {\theta }_{\sigma }\left(x,t\right)}{\partial t}<<{\omega }_0$

and

$\frac{1}{{\overline{n}}_{\omega }^{eff}\left(x,t\right)}\frac{\partial {\overline{n}}_{\omega }^{eff}\left(x,t\right)}{\partial x}<<k_{\omega }^{eff}\left(x,t\right),$

Here ${\theta }_{\sigma }\left(x,t\right)$ is the volume fraction of $\sigma$ - phase, as well as conditions for applying the approximation of the effective [52] macroscopic field

${\lambda }_{\omega }^{eff}\left(x,t\right)=\frac{2\pi {\upsilon }_{\omega }^{eff}\left(x,t\right)}{{\omega }_0}>>l$

in the expressions for determining the effective electrophysical properties [38] of the porous material according to the method of local spatial averaging.

Here $k_{\omega }^{eff}\left(x,t\right)=2\pi /{\lambda }_{\omega }^{eff}\left(x,t\right)$ and ${\upsilon }_{\omega }^{eff}\left(x,t\right)=c_0/{\overline{n}}_{\omega }^{eff}\left(x,t\right)$ are the wave vector and phase velocity of electromagnetic (T.E.M. – TransverseElectro Magnetic [53]) wave propagation into the modeled porous dielectric environment ${\overline{n}}_{\omega }^{eff}\left(x,t\right)$ , is the effective value of refractive index, ${\theta }_{\sigma }\left(x,t\right)$ is the volume fraction of $\sigma$ - phase, ${\omega }_0$ is the constant angle frequency of symmetric microwave irradiation and $l$ is the characteristic (R.E.V. – Represenatative Elementere Volume [39]) length of averaged volume.

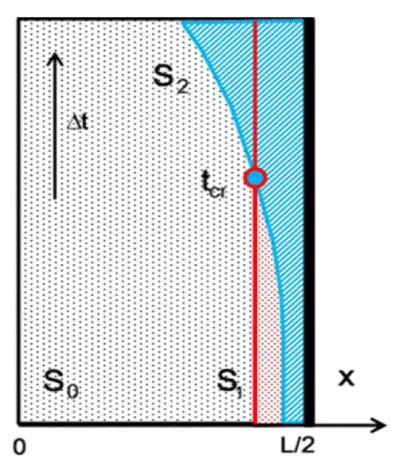
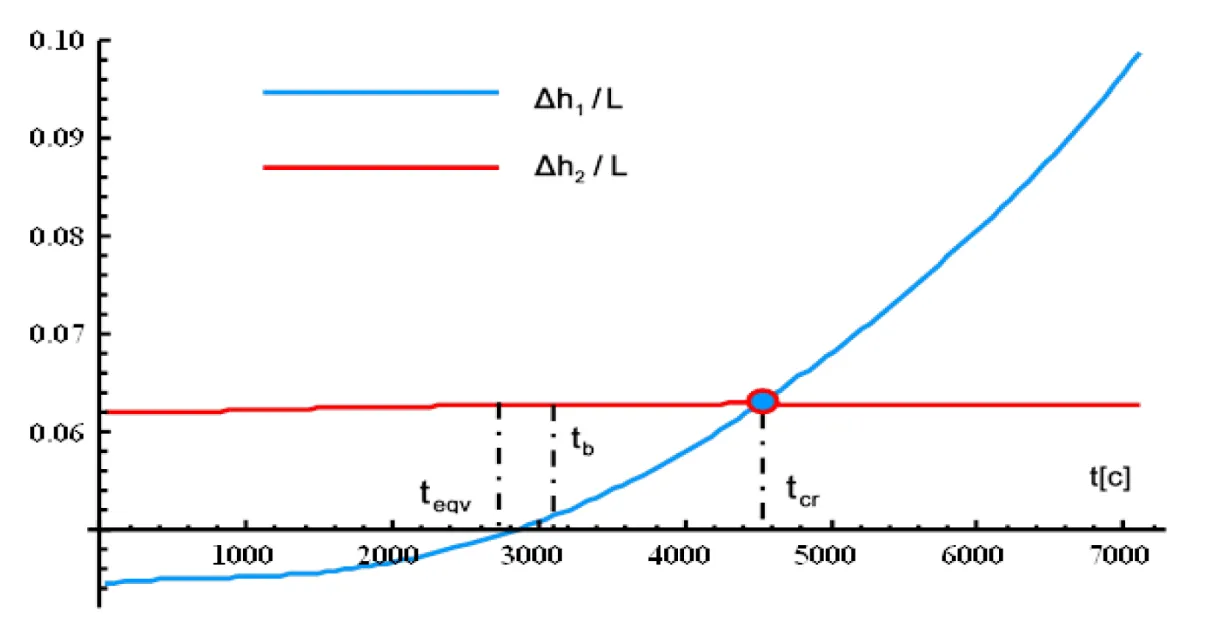
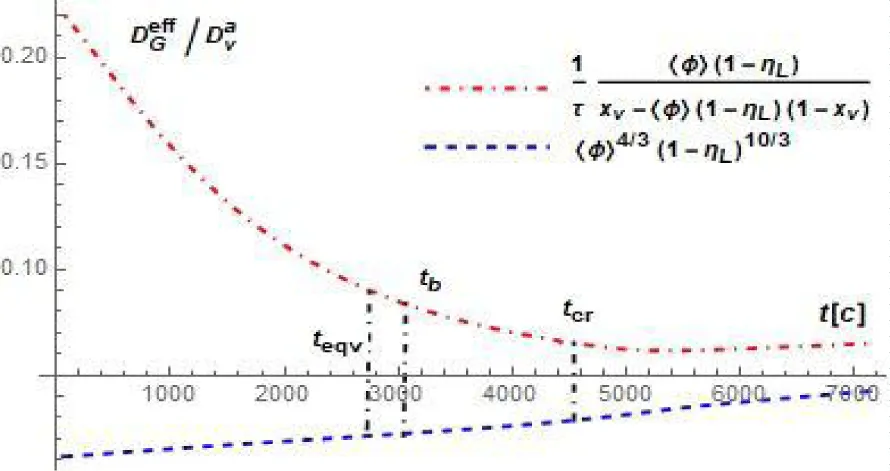
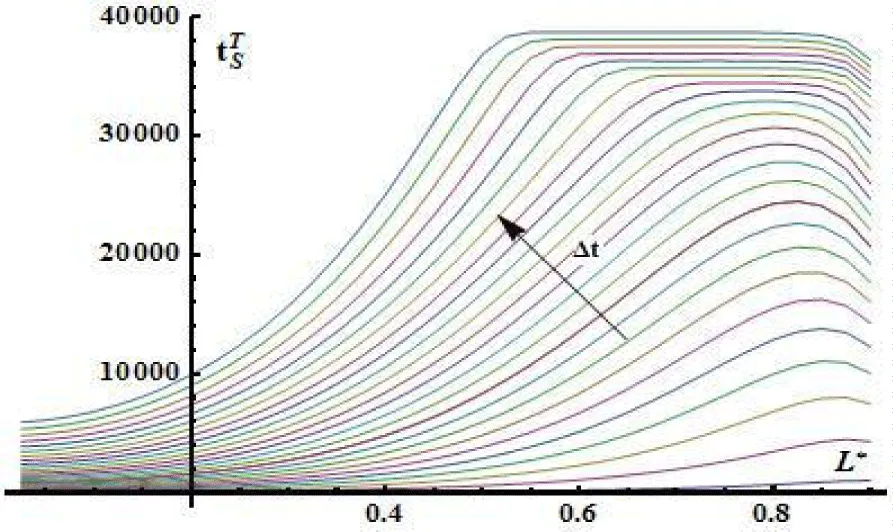
According to results of heat and mass process numerical simulation, the time shift of near-surface wetted and heated zones, which are separated by the surfaces $S_1$ and $S_2$ is obtained due to distribution of dimensionless sickness $\Delta h_1/L$ and $\Delta h_2/L$ (1) as depicted on figure 2) and (Figure 3) relatively to the surface $S_0$ of plate symmetry.

Conclusion I

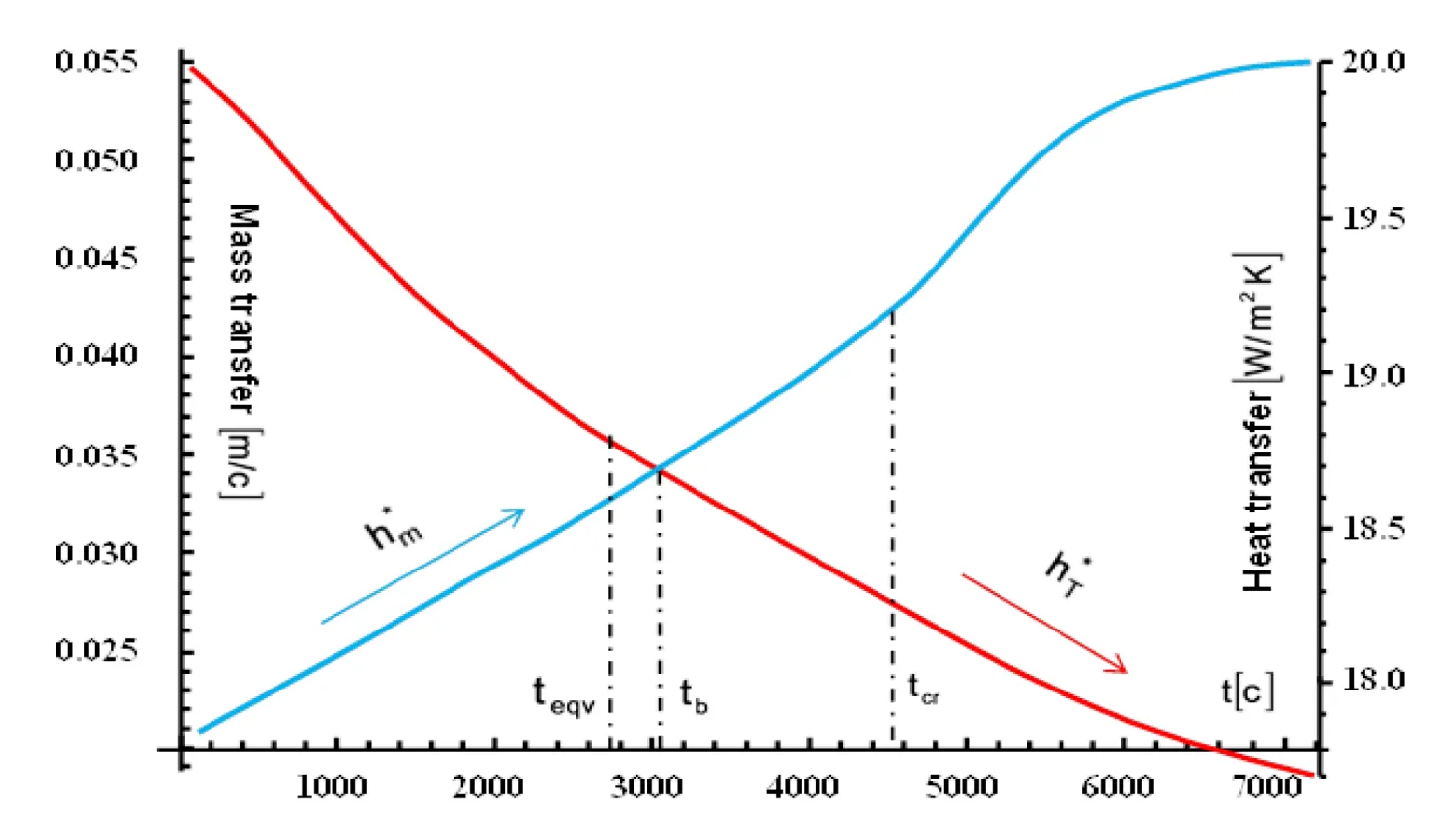
It is existing a fixed critical value of a time $t_{cr}$ there is a point of the crossover of surfaces $S_1$ and $S_2$ about that, the surface mass transfer coefficient $h_m^{*}$ (Figure 4) increases non-linearly. It can be joined with the beginning of the processes of intensity liquid evaporation at the near surface wetted zone;

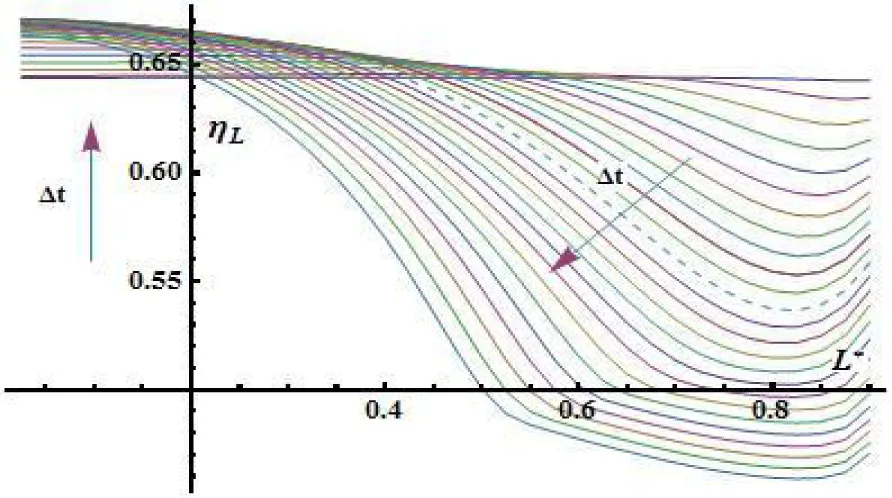
Likewise, it is also not significal the nonlinear behavior of the surface heat transfer coefficient is delivered $h_T^{*}$ (Figure 5) along the surface $S_1$ , which is produced with a deviation of the averaged liquid pore saturation ${\eta }_L$ from an equilibrium values at the surface of the symmetry $S_0$ of plate.

Conclusion II

In the neighborhood of time value $t_{eqv}$ an equilibrium state of a two component mixture of water vapor and dry air is fixed; above $x_{\nu }=x_a\simeq 1/2$ it the dry air is gradually displaced through the surface $S_1$ of wetting, and the molar fraction of water vapor $x_v$ in at the critical point of time $t_{cr}$ follows to the maximum value $x_{\nu }=1$ of saturation.

The diffusivity $D_G^{eff}/D_{\nu }^a$ of gas mixture in pores of material for the internal volume of the plate and at the evaporation surface are defined in various ways (here $D_G^{eff}$ is the diffusion coefficient of the gas mixture into pores and $D_{\nu }^a$ is the diffusion of water vapor into dry air), but over time in the region $t\ge t_{cr}$ the calculated values (at $\tau =4$ this porous body tortosity factor) of diffusion coefficients at the surface $S_1$ are aligned.

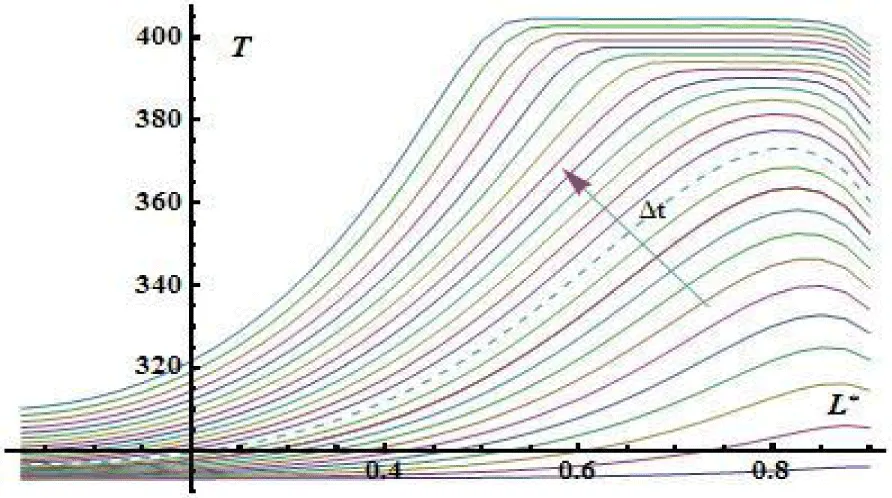
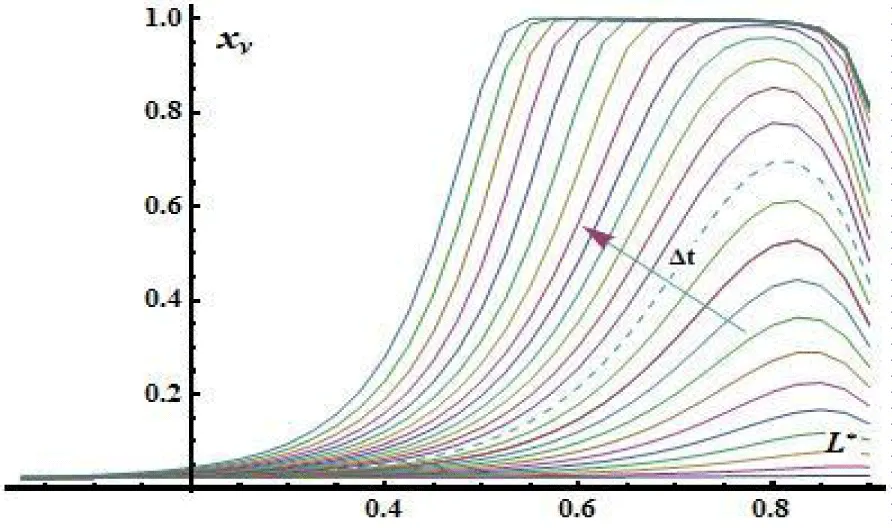
Solutions of the modified system of heat and mass transfer equations [50,51] for the material of historical ceramic brick are represented in the form of graphical dependencies as it is shown below, $L^{*}=n^{*}\Delta L/L_0\left(n^{*}=\Delta L/L_0\right)$ here is dimensionless half thickness of plate (Figures 6-8).

Conclusion III

Decreasing of moisture content is caused by the increasing of evaporation sources that are a result of inhomogeneous microwave heating of the plate and change of the thermodynamic state of two component mixture.

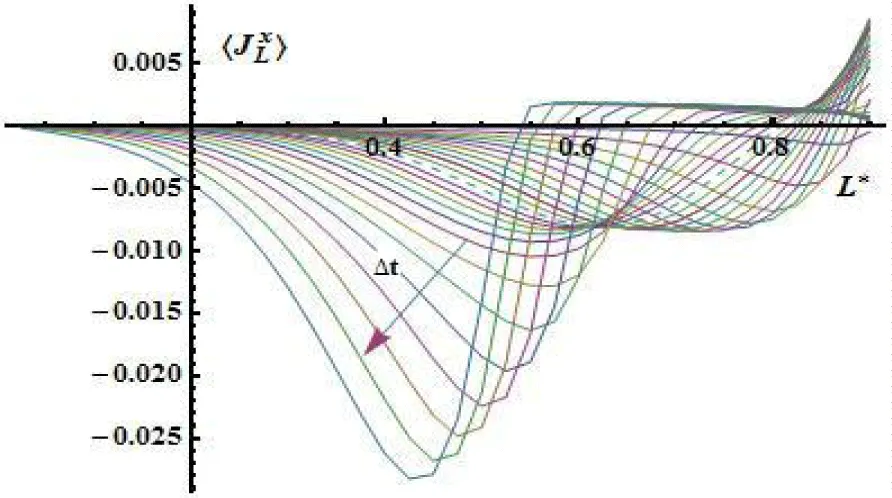
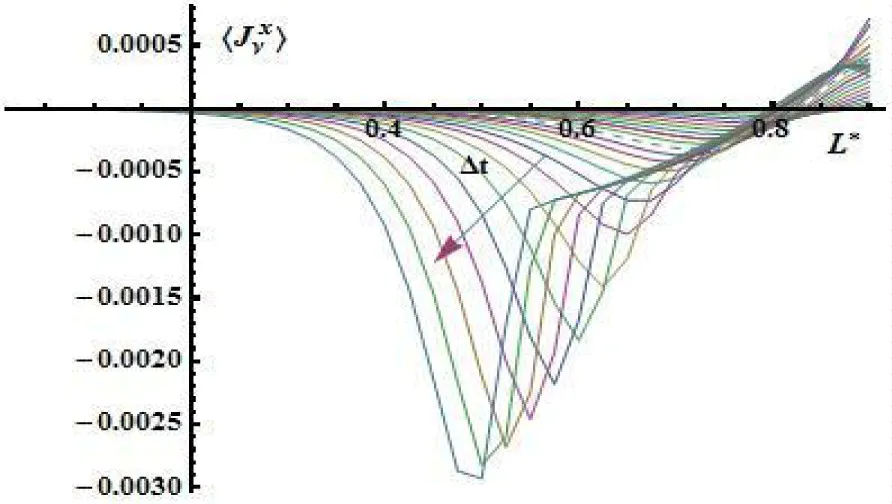
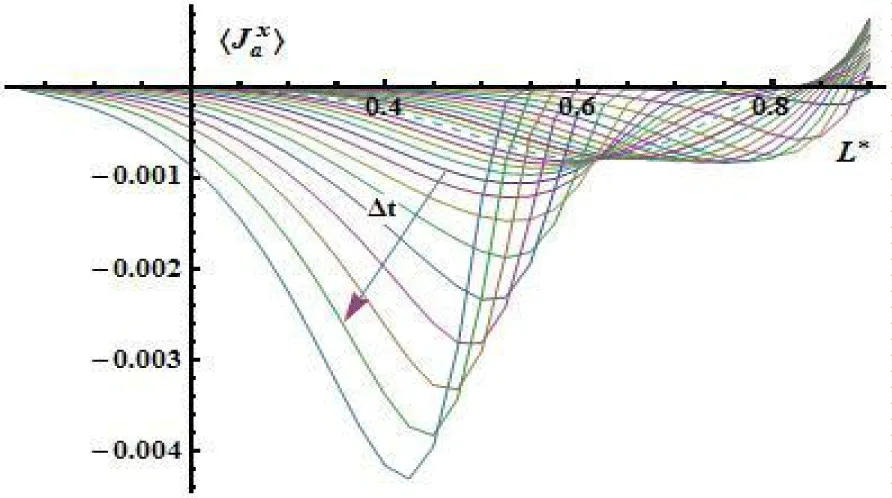
On the pictures below, it's depicted the distribution of flows by liquid $J_L^x$ (Figure 9), water vapor $J_{\nu }^x$ (Figure 10-12) and dry air $J_a^x$ (Figure 13) along half the thickness of the plate in the different time intervals.

Conclusion IV

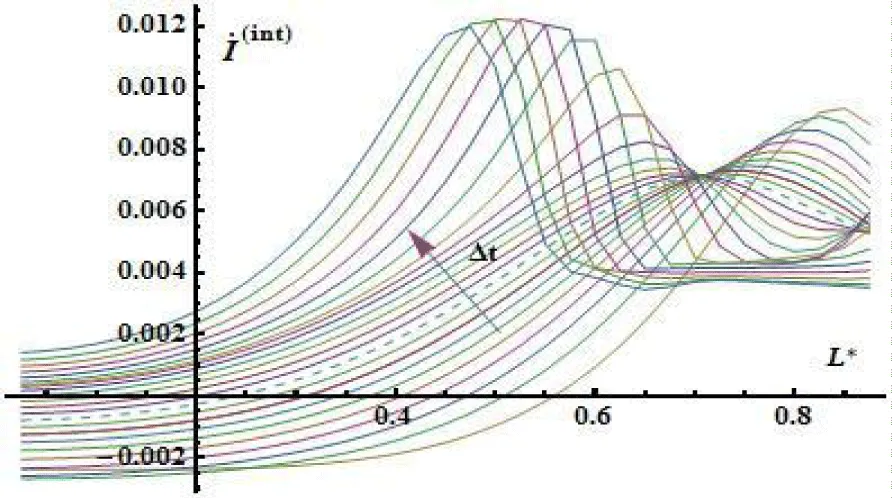
In the neighborhood of a time point $t_b$ that correlates to achievement of boiling temperature at normal conditions, its fixed changes of flow distribution for liquid and gas mixture components by the thickness of the plate (dashed line). This is due to an increase in the intensity (Figure 12) of internal sources of evaporation ${\stackrel{.}{I}}^{\left(int\right)}$ along the thickness of the plate.

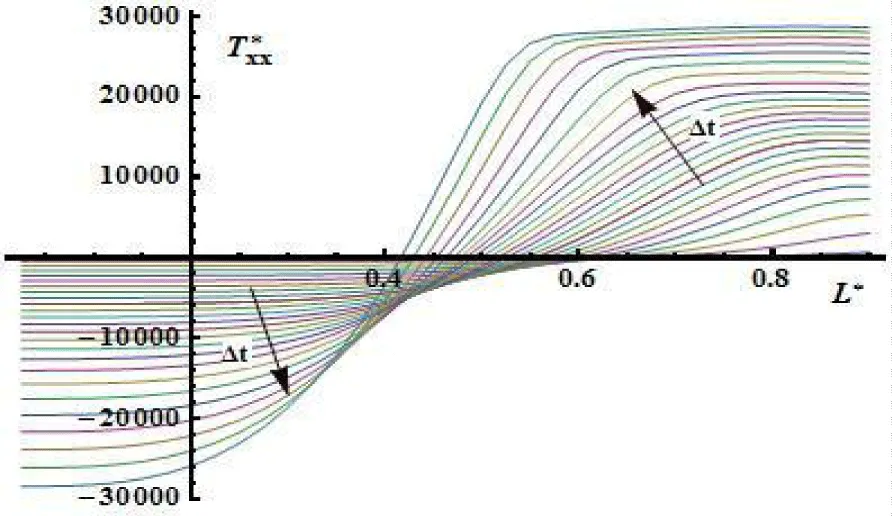
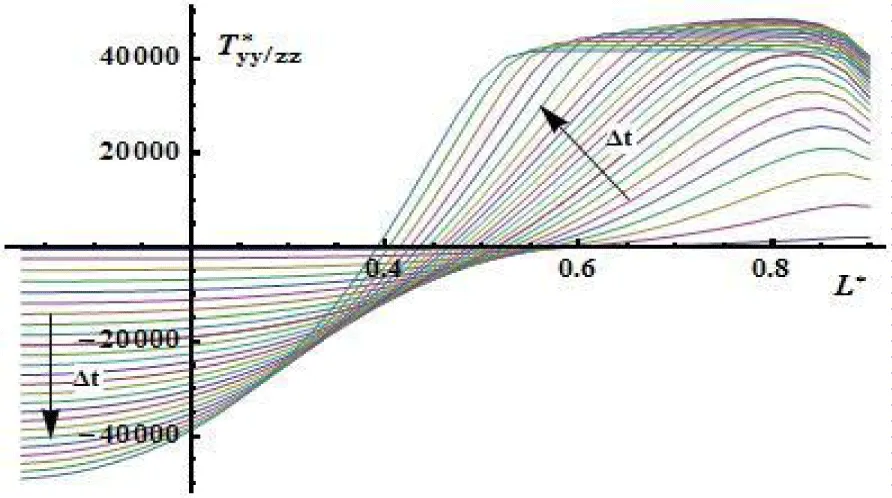
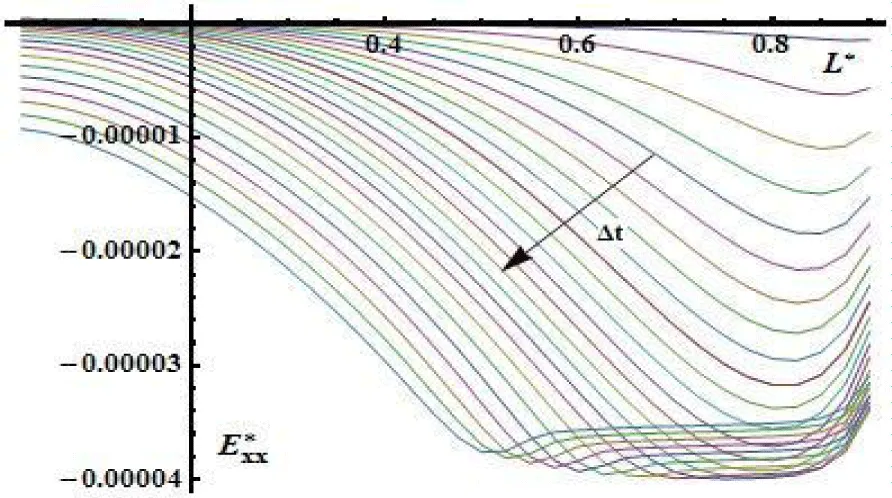
The distribution of specific stresses $T_{xx}^{*}$ (Figure 14) and $T_{xx/zz}^{*}$ (Figure 15) and small deformations $E_{xx}^{*}$ (Figure 15) and $E_{xx/zz}^{*}$ (Figure 16) in a solid matrix (frame or skeleton) over the half-thickness of the plate is shown by the following graphical dependencies (Figure 17).

The dynamics of thermal stress distribution $t_S^T$ (Figure 18) along the thickness of the plate is also shown in the form of the corresponding graphical dependence

From the pictures below see figures 14,15 it is follows that longitudinal components of stress tension are joined first with the distribution of the temperature field (Figure 7) and nonlinear behavior of the tangential component of stress tension is results of influence of the nonlinear evaporation processes (Figure 6) especially near the surface of sample.

The main advantage of the reviewed method for computer modelling of internal heating into this scientific mini repot is that under microwave treatment of porous heavily moisturized sample due to specific boundary conditions and linear combination of heat and mass transfer equation only hydraulic components of phase flows are considered under conditions of immediately transferring of liquid phase (water) into gas phase (water vapour) at the surface of evaporation. It is getting the possibility of applying such modelling to the medical industry for heating biological objects without damaging their internal structure. For example, as the acceleration of heating human transplant organs after Static Cold Storage (SCS) or worming of damaged tissues after cryoablation (freezing) during immunotherapy for threat tumours under the extreme medical human conditions. As it was seen from the mentioned above results of the computer simulation, there is no significant stress state, which corresponds basically to the changes in thermal properties of the porous skeleton. In the case of biological tissue, the internal heating mode can be regulated not only by the thickness of the sample but also through the changing of power and frequency of external microwave irradiation.

1. Samarskii AA. The theory of difference schemes. Moscow: Nauka. 1989;616.
2. Marchuk GI. Methods of computational mathematics. Moscow: Nauka. 1989;608.
3. Shi D. Numerical methods in heat transfer problems. Moscow: Mir. 1988;544.
4. Lindell IV. Methods for electromagnetic field analysis. Piscataway NJ. IEEE Press; 1995. p.320.
5. Desai RA, Lowery AJ, Christopouls C, Naylor CP, Blanshard JMV, Gregson K. Computer modelling of microwave cooking using the transmission-line model. IEEE Proc A. 1992;139:30-38.
6. Dibben DC, Metaxas AC. Finite element time domain analisys of multimode applicators using edge elements. J Microwave Power Electomagnetic Energy. 1994;29:242-251. doi: 10.1080/08327823.1994.11688252.
7. Iskander M. Modeling the microwave process - Challenges and new directions. Ceramic Trans. 1993;36:167-199.
8. Jia X, Jolly P. Simulation of microwave field and power distribution in a cavity by a three-Dimensional fi-nite element method. J Microwave Power Electomagnetic Energy. 1992;27:11-22.
9. Lorenson C. The why’s and how’s of mathematical modelling of microwave heating. 1990;11:P.14-22. doi: 10.20944/preprints202505.0265.v1.
10. Lorenson C, Gallerneault C. Numerical method for the modelling of microwave fields. Ceramic Trans.1991;21:193-200.
11. Davis J. Finite element analysis of waveguides and cavities – A review. IEEE Trans Magnetics. 1993;29:1578-1583.
12. Swinehart J. The Beer-Lambert law. J Chem Educ. 1962;39(7):333.
13. Chen DS, Sing RK, Haghighi K, Nelson P. Finite element analysis of temperature distribution in micro-wave cylindrical potato tissues. J Food Engineering. 1993;18:351-368. doi: 10.1016/0260-8774(93)90052-L.
14. Lin YE, Anantheswaran RC, Puri VM. Finite elment analysis of microwave heating of solid foods. J Food Engineering. 1995;25:85-112. doi: 10.1016/0260-8774(94)00008-W.
15. Jansen W, Wekken B. Modeling of dielectrically assisted drying. J Microwave Power Electromagnetic Energy. 1991;26:227-236.
16. Thomas HR, King SD. Couplet heat and mass transfer in unsaturated soil. A potentially -Based solution. Int J Numerical Analytical Methods Geomechanics. 1992;16:757-773.
17. Ozilgen M, Heil JR. Mathematical modeling of transient heat and mass transport in a backing biscuit. J Food Proc Pres. 1994;18:133-148.
18. Wang N, Brennan JG. A mathematical model of simultaneous heat and moisture transfer during drying of potato. J Food Engineering. 1995;24:47-60. doi: 10.1016/0260-8774(94)P1607-Y.
19. Chen P, Pei DCT. A mathematical model for drying processes. Int J. Heat and Mass Transfer. 1989;32(2):297-310.
20. King CJ. Freeze drying of foods. Butterworth, London: CRC Press; 1971. p.86.
21. Chen P, Pei DCT. A mathematical model for drying processes. Int J Heat and Mass Transfer. 1989;32(2):297-310.
22. Berger D, Pei DCT. Drying of hygroscopic capillary porous solids - A theoretical approach. Int J Heat and Mass Transfer. 1973;16:293-302. doi: 10.1016/0017-9310(73)90058-6.
23. Jansen W, Wekken B. Modelling of dielectric assisted drying. J Microwave Power Electromagnetic Energy. 1991;26:227-236. doi: 10.1080/08327823.1991.11688161.
24. Lal R, Shukla MK. Principles of soil physics. In: Basel NY, editor. MarcelDekker Inc; 2004. p.717.
25. Philip JR, Vries DA. Moisture movement in porous materials under temperature gradients. Thans Am Geophys Union. 1957;38:222-232. doi: 10.1029/TR038i002p00222.
26. Raudkivi AJ, Van U`n N. Soil moisture movement by temperature gradient. J Geotechnical Engineering Division. 1976;102:1225-1244.
27. Thomas HR, King SD. Couplet heat and mass transfer in unsaturated soil. A potentially - Based solution. Int J Numerical Analytical Methods Geomechanics. 1992;16;757-773.
28. Majorata CE, Gawin G, PesaventoF,Schrefler ВA. The sixth international conference on computational structures technology. The third international conference on engineering computational technology. Civil-Comp press and imprint of Civil-Comp Ltd. Stirling, Scotlant. Czech Republic, Prague. 2002;4(6):30.
29. Lepers B, Putranto A, Umminger M, Link G, Jelonnek J. A drying and thermoelastic model for fast mi-crowave heating of concrete. Frontiers in Heat and Mass Transfer (FHMT). 2014;5(13):1-11.
30. Ong KCG, Akbarnezhad A. Thermal stresses in the microwave heating of concrete. Proceedings of the 31st Conference on Our World in Concrete & Structures. Thailand, Singapore. 2006;15.
31. Like Q, Young L, Jun D, Pengfei T. Thermal stress distribution and evolution of concrete particles under microwave irradiation. Journal of Engineering Sciences and Technology Review. 2016;9(3):148-154.
32. Sungsoontorn S, Rattanadecho P, Pakdee W. One-dimensional model of heat and mass transports and pressure built up in unsaturated porous materials subjected to microwave energy. Drying Technology. 2011;29(2):189-204. doi: 10.1080/07373937.2010.483029.
33. Zhu H, Gulati T, Datta AK, Huang K. Microwave drying of spheres: Coupled electromagnetics-multiphase transport modeling with experimentation. Part I: Model development and experimental methodology. Food Bioprod.Process. 2015;96:314-325. doi: 10.1016/j.fbp.2015.08.001.
34. Gulati T, Zhu H, Datta AK. Coupled electromagnetics, multiphase transport and large deformation model for microwave drying. Chem Eng Sci. 2016;156:206-228. doi: 10.1016/j.ces.2016.09.004.
35. Kumar C, Joardder MUH, Farrell TW, Karim MA. Investigation of Intermittent Microwave Convective Drying (IMCD) of food materials by a coupled 3D electromagnetics and multiphase model. Dry Technol. 2018;36:736-750. doi: 10.1080/07373937.2017.1354874.
36. Teleken JT, Quadri MB, Antonio PN, Oliveira APN, Laurindo JB, Datta AK, Carciofi BAM. Mechanistic understanding of microwave-vacuum drying of non-deformable porous media. Dry Technol. 2021;39(7):850-867. doi: 10.1080/07373937.2020.1728303.
37. Alpert Y, Jerby E. Coupled thermal-electromagnetic model for microwave heating of Ttemperature-dependent dielectric media. IEEE Transactions on Plasma Science. 1999;27(2):555-562. doi: 10.1109/27.772285.
38. Hachkevych OR, Terlets’kyi RF, Holubets’ TV. Calculation of effective electrophysical characteristics of moitened porous materials. Journ of Math Sci. 2010;168(5):699-711. doi: 10.1007/s10958-010-0020-0.
39. Howes AH, Whitaker S. The spatial averaging theorem revisited. Chemical Engineering Science. 1980;23(12):1613-1623.
40. Chen P, Pei DCTA mathematical model for drying processes. Int J Heat and Mass Transfer. 1989;32(2)2:97-310.
41. Berger D, Pei DCT. Drying of hygroscopic capillary porous solids – A theoretical approach. Int J Heat and Mass Transfer. 1973;16:293-302. doi: 10.1016/0017-9310(73)90058-6.
42. Bird RB, Stewart WE, Lightfoot EN. Transport phenomena (Second Edition). New York-Toronto: Jon Wiley & Sons, inc; 2002. p.928.
43. Hassanizadeh M, Gray WG. General conservation equations for multi-phase systems: 1. Averaging procedure. Advanced in Water Resources. 1979;2:131-141. doi: 10.1016/0309-1708(79)90025-3. doi: 10.1016/0309-1708(79)90025-3.
44. Hassanizadeh M, Gray WG. General conservation equations for multi-phase systems: 2. Mass, momentuma, energy and entropy equations. 1970;2:191-203. doi: 10.1016/0309-1708(79)90035-6.
45. Hassanizadeh M, Gray WG. General conservation equations for multi-phase systems: 3. Constitutive theory for porous media flow. 1980;3:25-40. doi: 10.1016/0309-1708(80)90016-0.
46. Нигматулин РИ. Основы механики гетерогенных сред. M: Наука; 1978. p.336.
47. Eringen AC. Mechanics of continua. New-York: J. Wiley & Sons; 1962. p.608.
48. .R. Hachkevych, R.F. Terletskyi, T.L. Kurnytskyi. Modeling and Optimization in Thermomechanics of Electrically Conductive Inhomogeneous Bodies. In: Ya.Y. Burak, R.M. Kushnir, editors. OLviv: 'Spolom'. 2007; 300(1,2): 184.
49. Datta AK. Porous media approaches to studying simultaneous heat and mass transfer in food processes Part I - Problem formulations. Journ of food enginireeng. 2007;80:80-95. doi: 10.1016/j.jfoodeng.2006.05.013.
50. Datta AK. Porous media approaches to studying simultaneous heat and mass transfer in food processes Part II – Property data and representative results. Journ of food enginireeng. 2007;80:96-110
51. Holubets TV, Terletskiy RF, Yuzevych VM. The analytical expressions to describe wave propagation and heat release during microwave treatment of porous inhomogeneous plate based on the w.k.b. solution model. Advances in Materials Science. 2011;1:69-81. doi: 10.2478/adms-2023-0005.
52. Landau LD, Lifshitz EM. Electrodynamics of continuous media. Moscow: Nauka. 1982;632.
53. Orfanidis SJ. Electromagnetic waves and antennas. Rutgers University. 2004;1413.