General Science Group 2025 May 10;6(5):417-432. doi: 10.37871/jbres2099.
Evaluating the Efficacy of Different SARS-Cov-2 Drug Targets Using the Topo-Geometrical Superposition Algorithm, Molecular Docking and Chemical Reactivity Frameworks
Alejandro Morales-Bayuelo1*, Valentina Pérez-Quiñones2, Zvikomborero Zinhumwe3 and Praveen Mallri4,5
2Colegio Médico Colombiano, Ministerio de Salud, Cali-Valle del Cauca, Colombia
3Department of Bioengineering, Hubei University of Technology, Wuhan, China
4Department of Zoology, Indira Ganshi National Tribal University, Amarkantak, Madhya Pradesh, India
5Research Associate, Department of Research and Development, Academy of Bioelectric Meridian Massage Australia (ABMMA), Queensland, Australia
- SARS-CoV-2 virus
- COVID-19 treatments
- Molecular docking
- Molecular quantum similarity
- Chemical reactivity indices
- Density functional theory
Abstract
Introduction: The COVID-19 pandemic, an urgent global public health emergency, has resulted in millions of confirmed cases and deaths. Global healthcare systems face significant strain as facilities struggle to manage hospital capacities amid supply shortages. RdRp functions as the essential enzyme for viral replication through respiratory particles. The Food and Drug Administration recognizes Remdesivir as the only approved drug for COVID-19, yet scientists continue to explore additional treatment options.
Methods: The research implemented Glide docking software to perform Standard Precision (SP) and Extra Precision (XP) simulations. The docking grid maintained default parameters for the IFD method, which focused on accommodating different receptor conformations targeting RNA-dependent RNA polymerase's binding pocket. Molecular Quantum Similarity Measure (MQSM) performed Quantum similarity analyses through ZAB quantitative measures that evaluated molecules based on their Density Function (DFs). The molecular quantum similarity (MQS) calculation required two operators: the Dirac delta function and the Coulomb operator. The chemical reactivity analysis involved determining four primary indices, namely chemical potential (µ), hardness (η), softness (S) and electrophilicity (ɷ), to assess ligand stability and electrophilic characteristics alongside reactivity. Fukui functions revealed local chemical reactivity sites of the ligands to provide complete information about their reaction patterns.
Results: The molecular docking analysis showed that ligands formed important bonds with particular residues inside the binding pocket through hydrogen bonds to GLU166 and CYS145. The protein residues develop essential binding interactions that stabilize ligands. The chemical reactivity assessments revealed global reactivity parameters such as each ligand's chemical potential, hardness and softness, and electrophilicity. The analysis with Fukui functions revealed the electrophilic and nucleophilic areas on ligands to understand their reaction behavior and binding process better.
Conclusion: The multi-method research approach integrates molecular docking quantum similarity analysis and chemical reactivity studies and delivers essential details about ligands targeting the SARS-CoV-2 RNA-dependent RNA polymerase. The research findings support crucial advancements in designing drugs for COVID-19 treatment through rational methods.
Introduction
Numerous countries worldwide are affected by the major global health crisis triggered by the COVID-19 pandemic, while millions of people have confirmed cases and thousands have died from the virus. Healthcare systems throughout different nations battled unprecedented challenges that led to medical supply shortfalls and excessive hospital workloads while exhausting their medical personnel. Global challenges persist in the fight against the pandemic because vaccines represent the primary solution. At the same time, many nations continue facing reluctance to vaccination and logistical problems with distribution and inadequate access to vaccines.
SARS-CoV-2, the virus responsible for COVID-19, exhibits a range of symptom severity in those infected. Most individuals experience mild to moderate symptoms and recover without needing specific treatment, but some develop severe cases that require medical intervention [1]. The virus spreads mainly through tiny liquid particles released from an infected person's mouth or nose during activities like coughing, sneezing, talking, singing, or breathing. These particles, including small aerosols and larger respiratory droplets, can be transmitted via close contact with an infected person or by touching contaminated surfaces and the face [2]. As an RNA-dependent RNA polymerase (RdRp), SARS-CoV-2 depends on this enzyme for replicating and transcribing its genome, making it a key focus for studying the virus's biology and developing antiviral treatments [3].
In the fight against COVID-19, several drugs are currently under investigation, but so far, only one has received FDA approval: Remdesivir (Veklury). This antiviral medication treats COVID-19 in adults and adolescents aged 12 and older and is typically administered intravenously to hospitalized patients [4,5]. To better understand how these drugs interact with the receptor's active site, this study employed Molecular Docking, Molecular Quantum Similarity (MQS), and various reactivity indices to evaluate remdesivir and other related compounds. These include Arbidol, Baloxavir marboxil, Letermovir (Prevymis), Nexavir (Sorafenib), Podophyllotoxin, Trifluridine, Valaciclovir (Valtrex), and Zanamivir (Relenza).
The Molecular Quantum Similarity (MQS) concept, introduced by Carbo-Dorca and colleagues, investigates the molecular similarities across different compounds. The method applies DFT with Molecular Quantum Mechanics and Quantum Chemistry to merge molecular docking operations with chemical reactivity indices [5]. The innovative approach has generated essential information about possible COVID-19 treatments while revealing the binding relationships between approved medications, including remdesivir and proposed ligands.
Methodology for Docking Studies
System preparation
In the docking experiment, the receptor structure was prepared following specific protocols, with the crystal structure of SARS-CoV-2 RNA-dependent RNA polymerase (PDB code 6M71) as the reference. The receptor structure was further refined using the Protein Preparation Wizard module from the Schrödinger Suite 2017-1, and the following adjustments were made:
- Optimization of the hydrogen bond network and refinement of the protein structure.
- Protonation state determination at physiological pH using the PropKa utility.
- Restraint-based molecular minimization via the Impact Refinement (Impref) module, where heavy atoms were constrained to maintain a low Root-Mean-Square Deviation (RMSD) from the initial coordinates [6-8].
On the other hand, the molecular structures of the compounds were built using the Maestro Editor (Maestro, version 11.1, Schrödinger, LLC). The LigPrep module produced 3D conformations Epic predicted to exist under physiological pH conditions. The energy minimization process was executed through Macro Model using the OPLS2005 force field for adequate structural optimization.
Molecular docking approach
Glide was used with default parameters and the Standard Precision (SP) model for the docking studies. The binding pocket of RNA-dependent RNA polymerase (RdRp) was defined by the following residues: GLY616, TRP617, ASP618, TYR619, LEU758, SER759, ASP760, ASP761, ALA762, LYS621, TYR799, TRP800, GLU811, PHE812, CYS813, and SER814. These residues were identified using Glide's docking protocol [9,10]. The docking protocol used Glide scoring and prime advanced conformational refinement as part of its structured four-step workflow.
Initial docking: Glide performs rigid receptor docking to generate a range of ligand poses.
Side-Chain Prediction and Minimization: The protein is sampled using Prime’s side-chain prediction module, and the poses are minimized for each protein-ligand complex. Redocking: The ligand is redocked into the low-energy, induced-fit structures from the previous step using Glide’s default parameters (without van der Waals scaling). Binding Energy Estimation: The IFDScore, which includes docking energy (GScore), receptor strain, and solvation terms (from Prime energy), is calculated to estimate binding affinity. The degree of residue movement induced by the IFD process is further considered to investigate the active site's ligand interactions. All poses are compared within the molecular set for the most and least active ligands. Additionally, Molecular Dynamics (MD) simulations over 30 ns are performed to predict the most stable poses and evaluate their stability in the active site.
Quantum Similarity Analyses
Molecular quantum similarity measure
A Molecular Quantum Similarity Measure (MQSM) amid two A and B systems, known as ZAB, compares two molecules that may be created using their respective Density Functions (DFs).
Both DFs can be multiplied and integrated in terms of their electronic coordinates, which are then weighted using a predetermined positive operator Ω(r1,r2) [11-13]:
Equation 1 depends on the operator to evaluate information comparison and determine the level of system similarity. For example, using the Dirac delta function as the operator is particularly effective for functions with sharp peaks, like electronic density. It also provides a mathematical abstraction similar to a point charge or point mass, expressed as Ω(r1,r2)= δ(r1- r2).
One of the initial similarity metrics utilized is the overlapping MQSM, while another commonly employed alternative is the Coulomb operator, given by Ω(r1,r2)= |r1- r2|⁻¹, resulting in a Coulombic MQSM. Even when comparing two equivalent molecules, a similarity measure can be applied to any pair of molecular systems; this measurement is referred to as a self-similarity measure (ZAA for molecule A) [12].
For a given set of N molecules, a similarity measure can be computed for each molecule relative to every other molecule in the group, including itself. These similarity measurements can then be used to construct a symmetric matrix. The i-th column of this matrix represents the similarity measurements between the i-th molecule and all other molecules in the group, including itself. Thus, each column (vector) serves as an N-dimensional representation of the i-th molecule. These vectors can be viewed as a collection of chemical descriptors. Unlike traditional molecular descriptor sets used in theoretical descriptions, the columns of this similarity matrix offer a unique and distinctive representation of each molecule's properties [12-20].
- It is universal, derived from any collection of molecules and any individual molecule within that group.
- It is impartial, with no other possibilities available in the construction process than those dictated by the density functions and similarity measurements involved.
Carbó's similarity index
Carbó's similarity index for two molecules, I and J, is calculated using Equation 2. Known as the cosine similarity index, this measure represents the cosine of the angle between the density functions when they are considered as vectors. For any pair of compared molecules, the Carbó QSI ranges from 0 to 1, reflecting the degree of similarity between them, with a value closer to 1 indicating greater similarity (i.e., when I is identical to J) [13-28].
The quantum similarity using the Euclidean distance
Taking into account the similarity of equation 3:
It is simplified to the so-called Euclidean distance index when k= x= 2. Index 3 of the form can also be defined as follows:
This Equation 4 forms the distance index of infinite order [18-30].
MQSM overlap considering the equation 2:
The distribution of Dirac's delta, Ω (r1, r2) = δ (r1, r2), is the most typical and intuitive choice for such a positively defined operator. These selections transform the broad definition of MQSM to compute the overlap MQSM that obtains volume measurements by both electronic density functions when superimposed [17-20].
The Dirac delta function is derived instinctively from the physical definition and is computationally compliant. The MQSM calculates the degree of overlap between molecular comparisons using information about the electron concentration in the molecule [16-21].
MQS Coulomb Considering the Equation 5
When the operator (Ω) is replaced with the Coulomb operator, Ω (r1, r2) = , the coulomb MQS is generated, which defines the electrostatically repellent coulomb energy between two charge densities [20,21]:
The equation enables expansion of the Coulomb operator through molecular density functions, which show electron distributions in space. As such, it can serve as a descriptor for electrostatic potential in specific contexts. This operator is related to electrostatic interactions and measures the electrostatic repulsion between electronic distributions [30-37].
Euclidean distance index considering the equation 3
Another major transformation that can be expressed in terms of the classical distance is:
Here is the distance between a and b, and k=2 is the definition of distance, respectively. Subsequently, the Euclidean distance between A and B as two quantum objects is defined by [17-21]:
Occasionally, it is written as: , where DAB has values in the range of [0,∞﴿ but for earlier circumstances where the compared items are identical, it converges to zero between them [17-21]:
The norm of the differences in the density functions of the compared objects can be used to interpret this index geometrically. The distance or dissimilarity index can be used to define the Euclidean distance index, which can also be represented as [21-25]:
Alignment method - TGSA (Topo-Geometrical Superposition Algorithm)
Gironés developed TGSA to apply molecular superposition theory to shared frameworks through atomic type matching and bonding interactions based on atomic number coordination principles [23-35].
Chemical Reactivity Analysis
The field established that quantum similarity corresponds directly with chemical reactivity descriptors [37,38]. Both quantum similarity and DFT require the density function to calculate similarity indices. Chemical reactivity utilizes the Coulomb index as its electronic basis to achieve its effects. FMO analysis that accounts for the energy gap is required to compute global reactivity indices μ, ɳ, and ω [39-44].
Results and Discussion
Molecular docking>
The COVID-19 virus responsible for SARS-CoV-2 undergoes regular mutations, which create new variants that make drug development more difficult. Developing treatments that work on different virus strains represents a principal barrier. The quick virus spread, and immediate treatment requirements make it hard to adhere to standard drug development timelines. Rush processes needed during emergencies might lead to reduced testing procedures and validation routines.
Despite these challenges, the scientific community has made significant strides, rapidly developing vaccines and exploring various therapeutic strategies. Ongoing research and global collaboration will be crucial for addressing the evolving nature of the pandemic and improving our ability to manage and treat COVID-19.
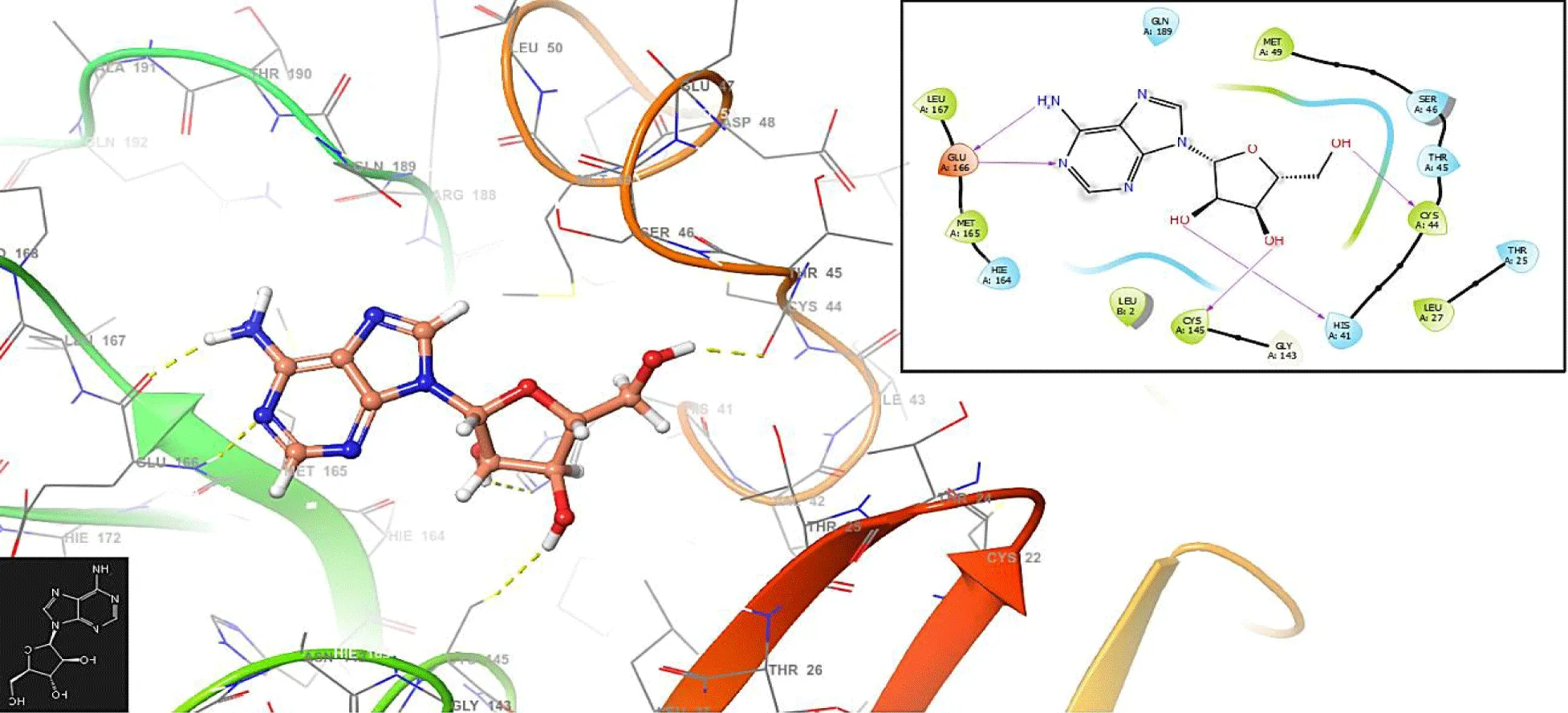
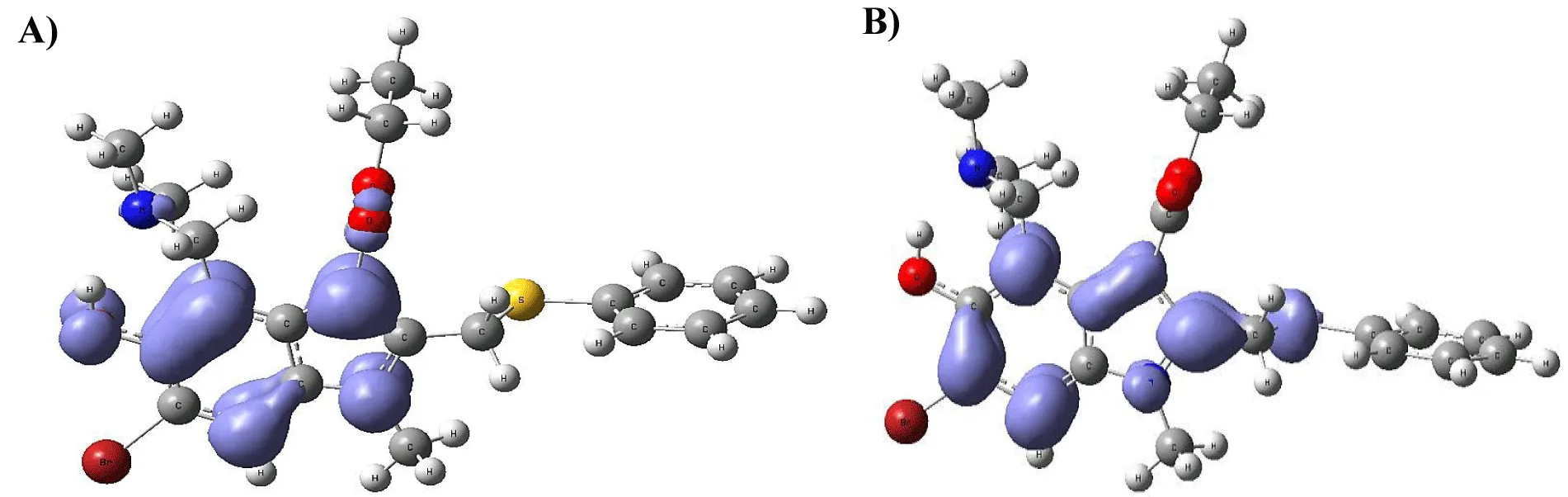
This study provides new insights into a series of ligands based on the crystal structure of SARS-CoV-2 RNA-dependent RNA polymerase (PDB code 6M71). Figure 1 presents the molecular docking results for the compound Vidarabine.
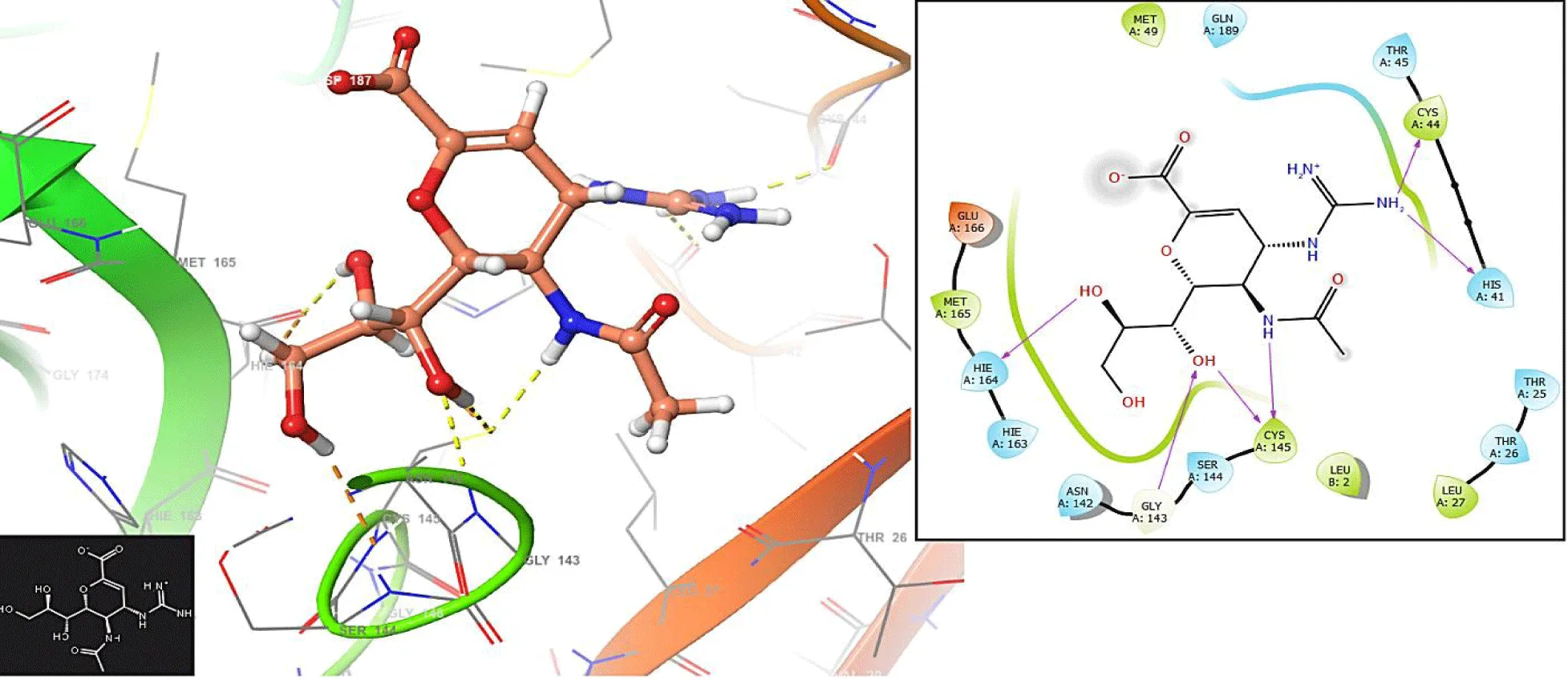
In figure 1, the Vidarabine has interaction with the residues GLU166 (-H bond: 1.2581 Å and 1.2846 Å), CYS145 (-H bond: 1.3658 Å) and HIS41: 1.458 Å.
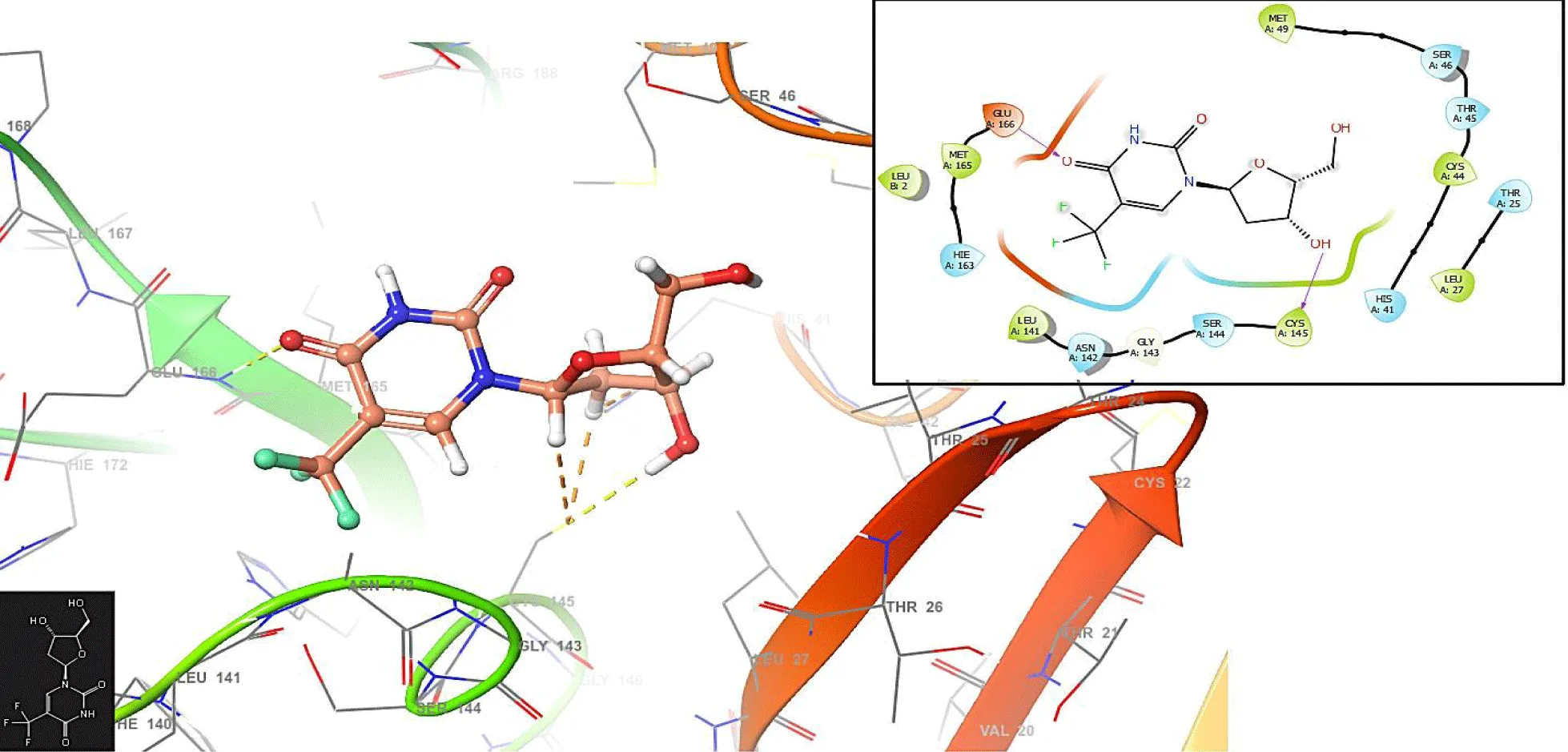
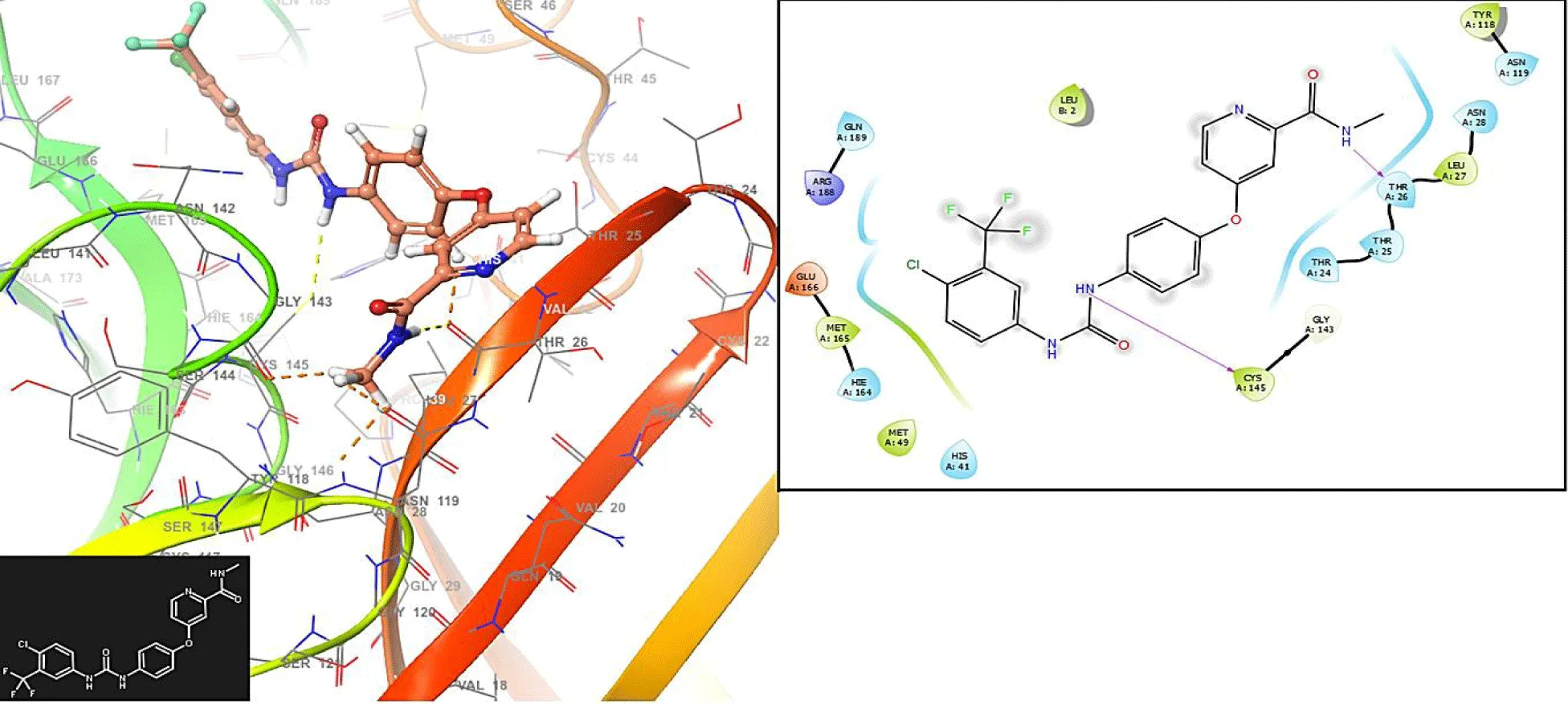
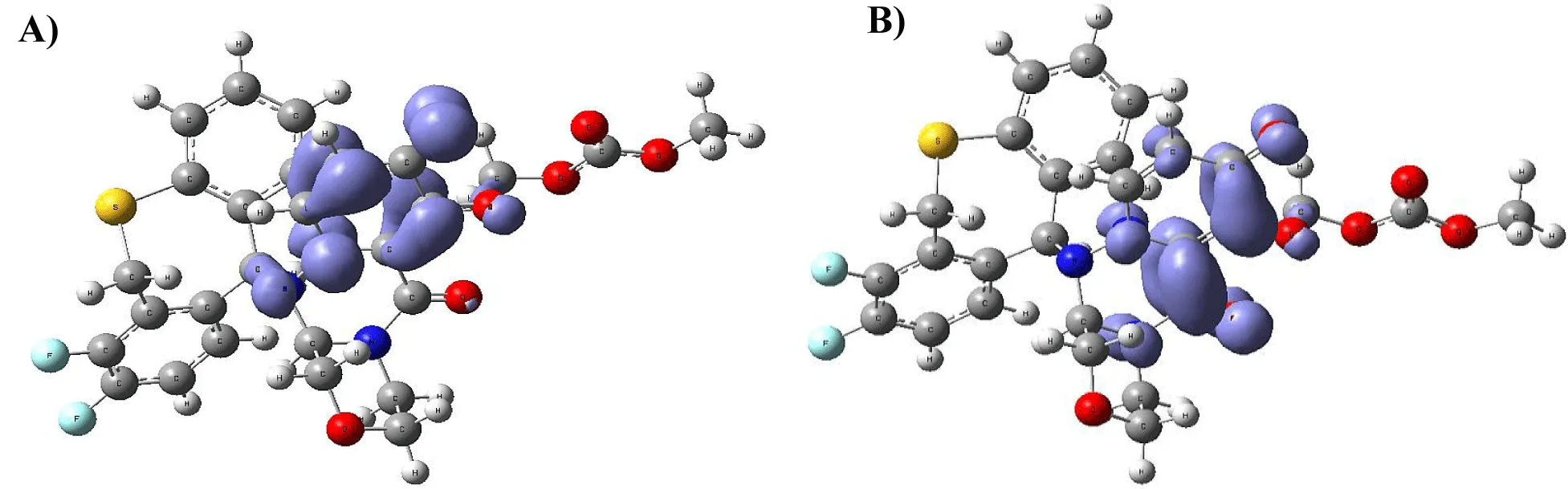
In figure 2, the Trifluridine interacts with the residues GLU166 (-H bond: 1.1281 Å) and CYS145 (-H bond: 1.0158 Å). In the same form, the Letermovir interacts with the residues GLU166 (-H bond: 1.3282 Å) and CYS145 (-H bond: 1.1285 Å and 1.3426 Å); (Figure 3).
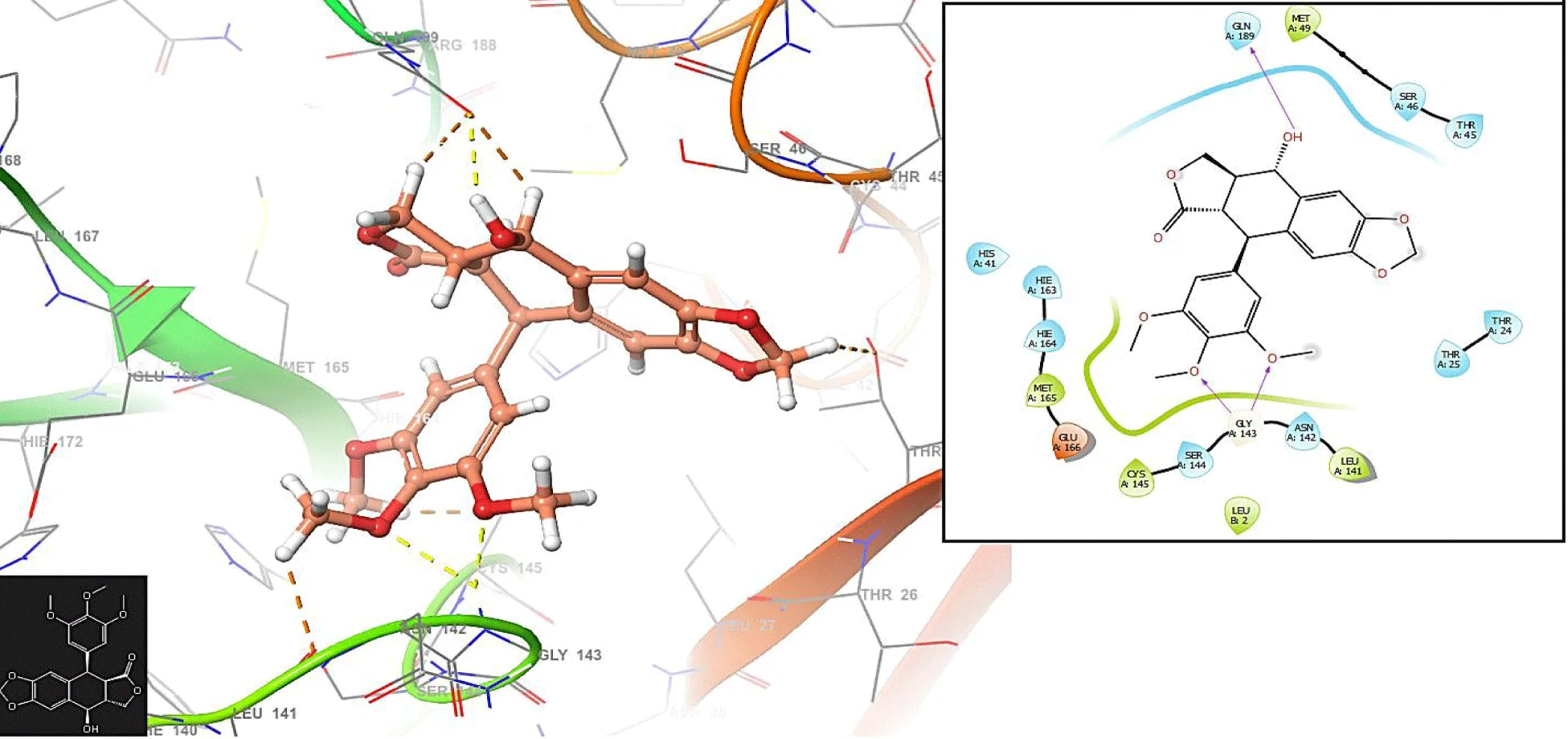
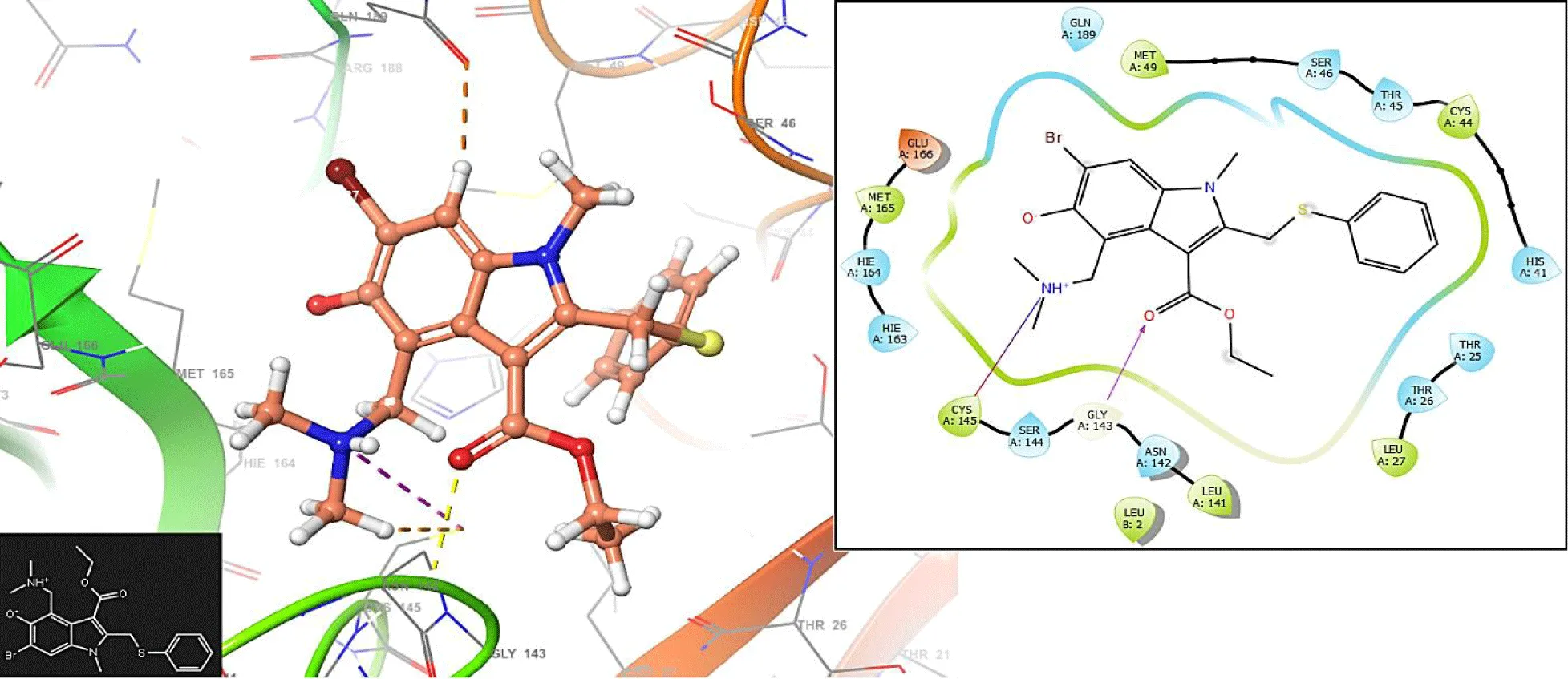
Unlike figures 1-3, the Podophyllotoxin has no interaction with the residues GLU166 and CYS145. The compound has an interaction with the residue GLN189: 1.2548 Å.
Researchers can use the identification of vital back pocket residues to create new drug development opportunities. The back pocket's structural stability relies on the contributions of the pocket's residue components. The evolutionary fitness of the virus depends on specific pocket residues remaining conserved during evolutionary changes across different virus strains. Medical research that targets invariant protein regions improves the potential for producing antiviral medications that work against diverse viral strains. The host immune system reacts to protein interactions within the back pocket region. Studying how viral proteins influence host immune pathways becomes essential because it enables researchers to develop approaches that boost the host immune defense against infections. When replicating viruses, they use existing cellular components from their host organisms. Back pocket residue interactions determine how the virus can adapt to and control host cellular processes and membrane transport functions. Coronaviruses and other viruses use different tactics to avoid detection by the host immune system during infection. Specific residues in the back pocket help viruses evade host defense systems; thus, researchers could use these interactions to improve immune response effectiveness.
Understanding the importance of interactions with residues in the back pocket of a protein related to COVID-19 is essential for unraveling the virus's molecular mechanisms and guiding therapeutic interventions and drug development efforts (Figure 4).
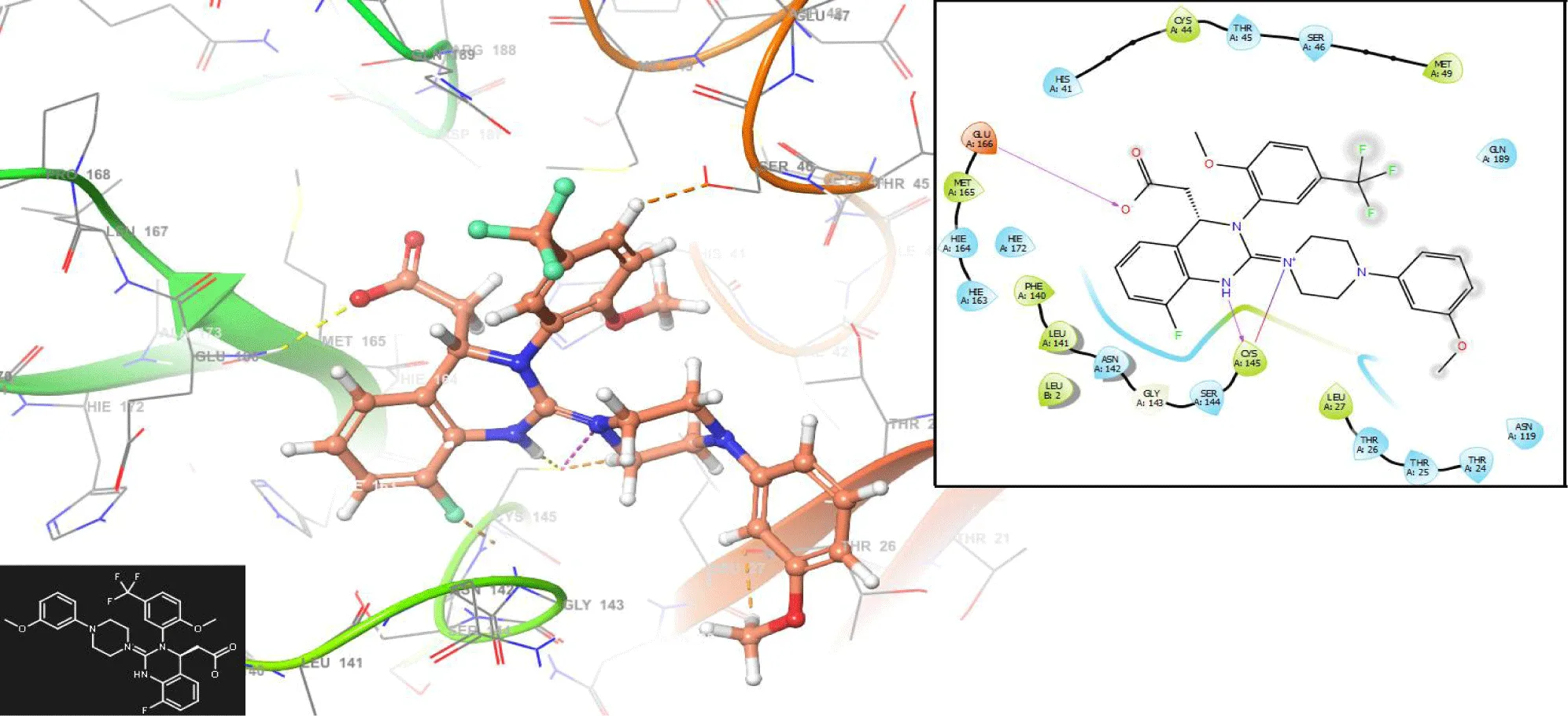
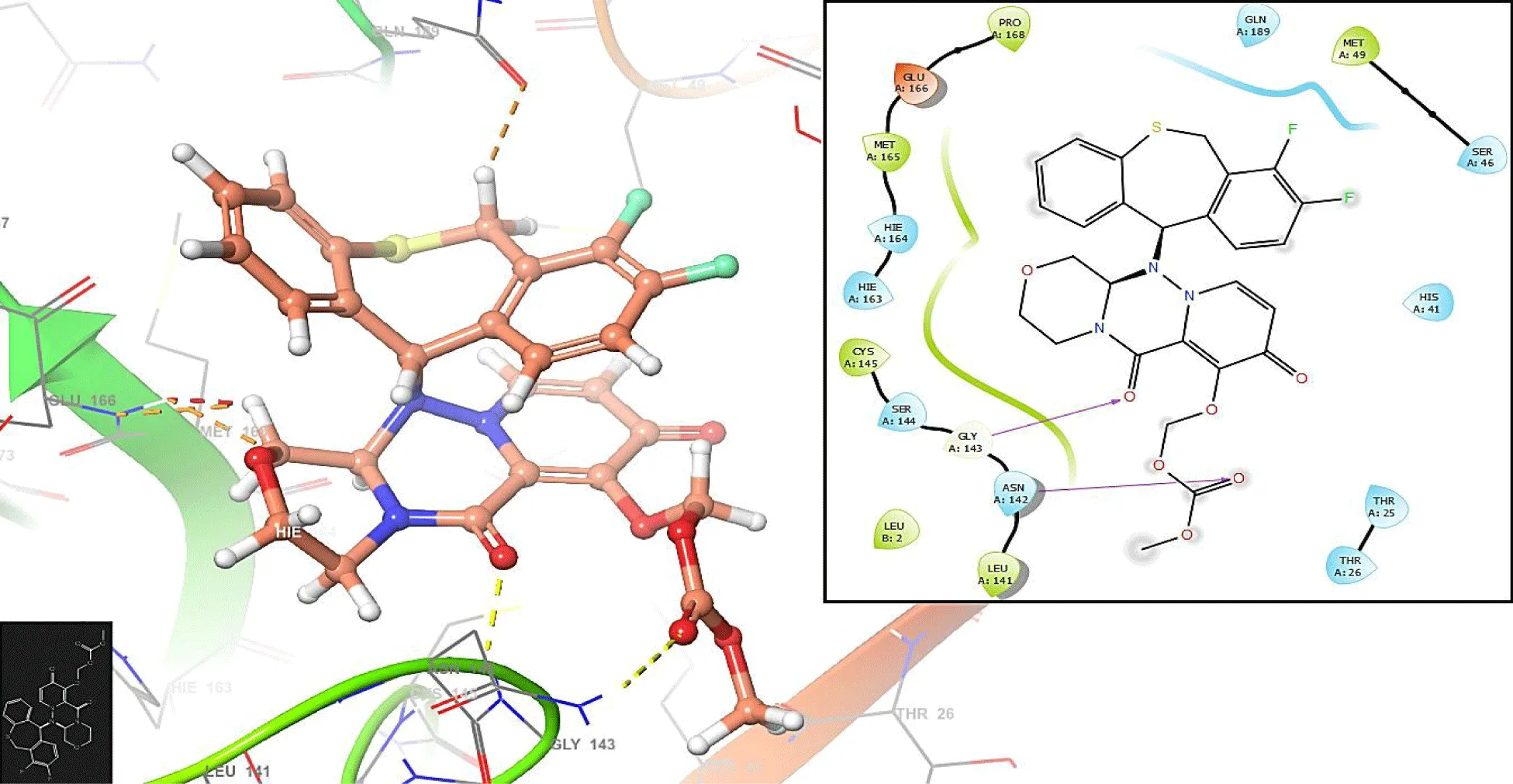
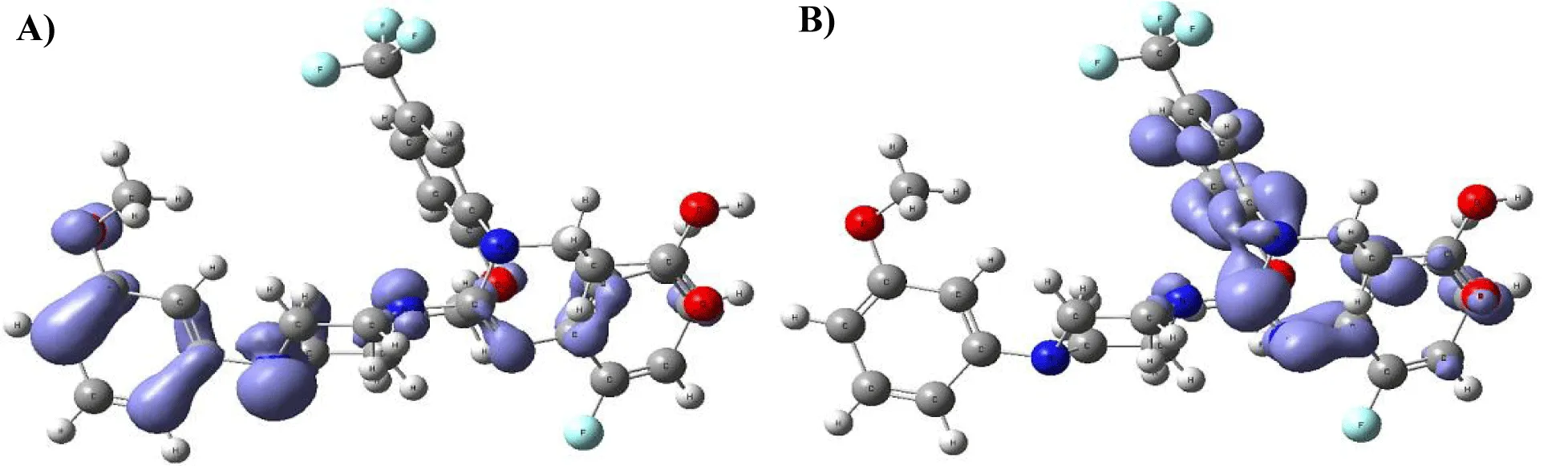
Figures 5,6 show the interactions with the compounds Nexavir and Baloxavir marboxil, respectively. Nexavir interacts with the residues CYS145 (-H bond: 1.3692 Å) and THR25 (-H bond: 1.1286 Å), while the compound Baloxavir marboxil interacts with the residues GLY143 (-H bond: 1.2486 Å) and ASN142 (-H bond: 1.3942 Å).
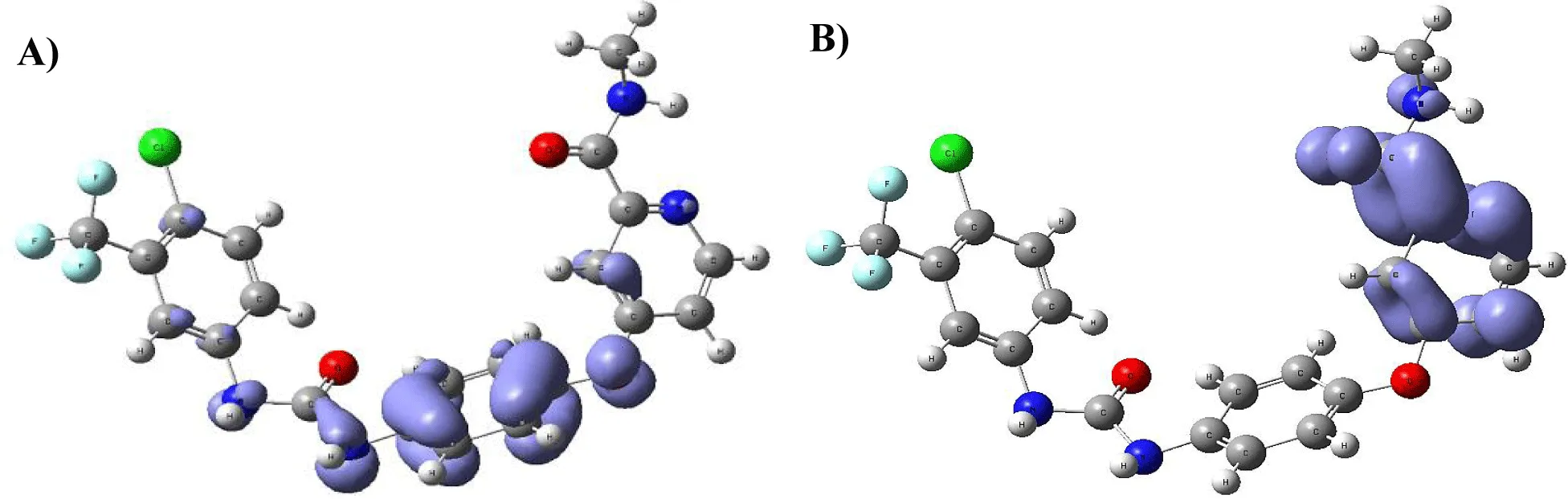
Figures 7,8 show the interactions with the compounds Zanamivir and Arbidol. The compound Zanamivir interacts with the residues HIE164 (-H bond: 1.3658 Å), GLY143: 1.2569 Å and CYS145: 1.1586 Å and 1.2564 Å.
Protein structures associated with COVID-19 require stable bonds between hydrogen molecules to maintain their structure. Hydrogen bonds help shape protein three-dimensional structures and serve as essential elements that support stable protein molecule stability. Hydrogen bonds are critical to building secondary protein structures because they produce alpha helices and beta sheets. The stabilizing forces of alpha helices occur when the carbonyl oxygen of one amino acid bonds to the amide hydrogen of an amino acid located a distance downstream, maintaining the helical shape. Beta sheets exist as stable structures because hydrogen bonds connect the adjacent strands. The solubility of proteins depends on hydrogen bond interactions between water molecules and polar amino acid side chains outside the protein structure. A protein maintains its stable solution environment through water molecules that interact with it. Hydrogen bonds are dynamic because they create and break apart, thus enabling proteins to shift their structures. The dynamic stability mechanism enables protein transition between functional states because enzymes need it to change between active and inactive states.
Quantum similarity analysis
In table 1, the higher overlap similarity is between the compounds Vidarabine-R vs Trifluridine-R with 0.5673 with a Euclidean distance of 4.5422 (Table 2) and the lowest similarity is between Zanamivir (Relenza)-R vs Letermovir-R with 0.1793 their euclidean distance of 7.5148. The similarity values are generally low (under 0.5), considering the interval related to the Carbo index (0.1).
| Table 1: Overlap molecular quantum similarity values. | ||||||||
| O_Hab | Arb | Lete | Nexa | Podo | Triflu | Vala | Vida | Zana |
| Arb | 1.0000 | |||||||
| Lete | 0.2985 | 1.0000 | ||||||
| Nexa | 0.3263 | 0.2009 | 1.0000 | |||||
| Podo | 0.3733 | 0.2713 | 0.2597 | 1.0000 | ||||
| Triflu | 0.3107 | 0.5107 | 0.4074 | 0.3278 | 1.0000 | |||
| Vala | 0.3331 | 0.2776 | 0.2742 | 0.2039 | 0.3342 | 1.0000 | ||
| Vida | 0.3685 | 0.2379 | 0.2417 | 0.2371 | 0.5673 | 0.3488 | 1.0000 | |
| Zana | 0.3086 | 0.1793 | 0.1795 | 0.3111 | 0.2734 | 0.2638 | 0.3212 | 1.0000 |
| Table 2: Euclidean distance using the overlap operator. | ||||||||
| O_Dab | Arb | Lete | Nexa | Podo | Triflu | Vala | Vida | Zana |
| Arb | 0.0000 | |||||||
| Lete | 6.8628 | 0.0000 | ||||||
| Nexa | 6.1639 | 7.7602 | 0.0000 | |||||
| Podo | 5.7267 | 7.2353 | 6.7469 | 0.0000 | ||||
| Triflu | 5.9138 | 5.9194 | 5.9685 | 6.1410 | 0.0000 | |||
| Vala | 5.5566 | 6.9379 | 6.3696 | 6.4222 | 5.7886 | 0.0000 | ||
| Vida | 5.2113 | 6.9548 | 6.3227 | 6.0894 | 4.5422 | 5.2632 | 0.0000 | |
| Zana | 5.8325 | 7.5148 | 6.9308 | 6.1351 | 6.2123 | 5.9916 | 5.5602 | 0.0000 |
On the Other hand, in table 3, we can see the higher electronic similarity between the compound Vidarabine-R vs., Trifluridine-R with 0.9529 with a Euclidean distance of 14.3644 (Table 4) and the lowest similarity between the compounds Vidarabine-R vs. Letermovir-R with 0.5901 and a euclidean distance of 61.1425. Unlike the overlap similarity values, the electronic similarity is above 0.5 with the Carbo index (0.1). Therefore, in the set studied, although the molecules are quite different from a structural point of view, they are quite similar from an electronic point of view.
| Table 3: Coulomb molecular quantum similarity values. | ||||||||
| C_Hab | Arb | Lete | Nexa | Podo | Triflu | Vala | Vida | Zana |
| Arb | 1.0000 | |||||||
| Lete | 0.8188 | 1.0000 | ||||||
| Nexa | 0.7329 | 0.7681 | 1.0000 | |||||
| Podo | 0.8689 | 0.7645 | 0.8005 | 1.0000 | ||||
| Triflu | 0.7811 | 0.8213 | 0.7429 | 0.8320 | 1.0000 | |||
| Vala | 0.8045 | 0.7885 | 0.6250 | 0.8210 | 0.7972 | 1.0000 | ||
| Vida | 0.7779 | 0.5901 | 0.6676 | 0.7416 | 0.9529 | 0.6885 | 1.0000 | |
| Zana | 0.8490 | 0.7389 | 0.7599 | 0.8167 | 0.6525 | 0.7626 | 0.6939 | 1.0000 |
| Table 4: Euclidean distance using the coulomb operator. | ||||||||
| C_Dab | Arb | Lete | Nexa | Podo | Triflu | Vala | Vida | Zana |
| Arb | 0.0000 | |||||||
| Lete | 43.8093 | 0.0000 | ||||||
| Nexa | 42.2388 | 48.4877 | 0.0000 | |||||
| Podo | 29.9169 | 48.8483 | 37.4501 | 0.0000 | ||||
| Triflu | 35.4518 | 45.7493 | 39.5504 | 33.1973 | 0.0000 | |||
| Vala | 33.8267 | 47.7126 | 47.6373 | 34.0725 | 30.7978 | 0.0000 | ||
| Vida | 35.5541 | 61.1425 | 44.0302 | 40.0380 | 14.3644 | 37.0406 | 0.0000 | |
| Zana | 30.0799 | 51.2319 | 38.8327 | 34.5350 | 41.2215 | 34.7385 | 37.7945 | 0.0000 |
Electronic similarity proves essential for drug design because it determines potential new drug candidates' performance, selectivity, and safety levels. The rational design of drugs requires a thorough understanding and efficient use of electronic similarity. Drug design heavily depends on electronic similarity because drugs must match their targets through binding affinity. Potent and specific biomolecule interactions result from electronic properties that match between drug molecules and their targets, thus producing effective binding events. Drugs require electronic similarity to achieve proper selectivity during their action mechanism. The selective interaction between drugs with electronic profiles and particular target proteins or receptors decreases unexpected drug effects, creating superior therapeutic benefits. The investigation of drug behavior at a molecular level often depends on electronic structure evaluations that quantum mechanical calculations help assess. Drug developers use these considerations to improve electronic characteristics for achieving specific drug activities.
Chemical reactivity study
Ligand stabilizing factors in proteins depend heavily on chemical reactivity indices. Researchers studying these indices learn about ligand-protein binding interactions that explain protein-ligand stability and specific and non-specific binding abilities. The bond strength between ligands and proteins depends on electronic and thermodynamic factors representing chemical reactivity indices. Ligands with advantageous electronic properties form robust bonds that improve their binding capabilities toward proteins. The propensity for electrophilic or nucleophilic reactions between ligands and particular amino acid residues in proteins depends on the reactivity indices of electrophilicity and nucleophilicity. The protein binding site becomes more stable due to the interactions that occur between ligands. Table 5 presents the global reactivity indices because of the highest similarity values derived from electronic perspectives.
Table 5: Chemical reactivity indices. |
||||
| Compound | C. Potential (µ) | Hardness (η) | Softness (S) | Electrophilicity (µ) |
| Arbidol | -3.1190 | 4.5868 | 0.2180 | 1.0604 |
| Letermovir-R | -3.5314 | 4.6572 | 0.2147 | 1.3388 |
| Nexavir | -3.9948 | 4.3340 | 0.2307 | 1.8411 |
| Podophyllotoxin-R | -3.5282 | 5.1293 | 0.1949 | 1.2134 |
| Trifluridine-R | -4.6889 | 5.0083 | 0.1996 | 2.1950 |
| Valaciclovir (Valtrex)-R | -2.8524 | 2.8428 | 0.3517 | 1.4311 |
| Vidarabine-R | -3.4062 | 4.8249 | 0.2072 | 1.2023 |
| Zanamivir (Relenza)-R | -3.6942 | 3.6001 | 0.2778 | 1.8954 |
Table 5 shows the values of the global reactivity indices. The compound with the highest chemical potential is Trifluridine-R with µ = -4.6889eV. The compound with the highest hardness is Podophyllotoxin-R, with η = 5.1293 eV. The compound with the highest softness is Valaciclovir (Valtrex)-R with S=0.3517 eV-1. Finally, the compound with the highest electrophilicity is Trifluridine-R with ɷ =2.1950 eV.
Electrophilic ligands may form strong interactions with nucleophilic sites on the protein, such as amino acid residues with electron-rich functional groups (e.g., nitrogen or sulfur atoms). The electrophilic nature of the ligand facilitates the formation of covalent or non-covalent bonds with the nucleophilic sites, contributing to higher binding affinity.
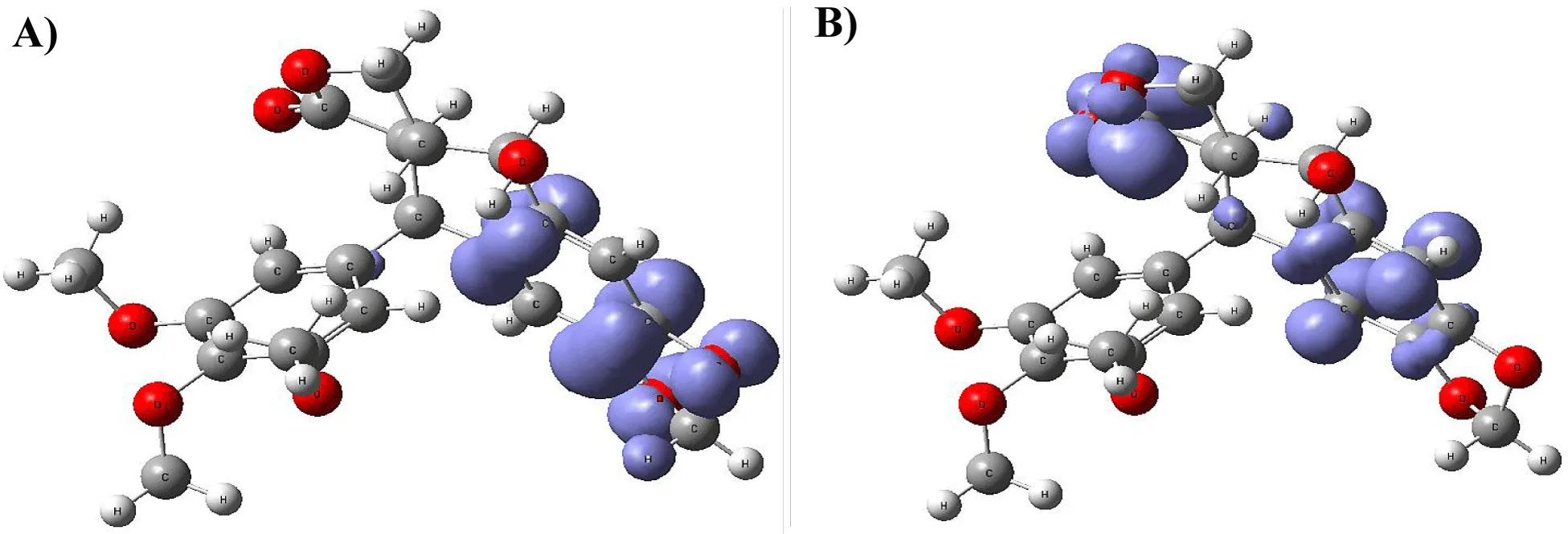
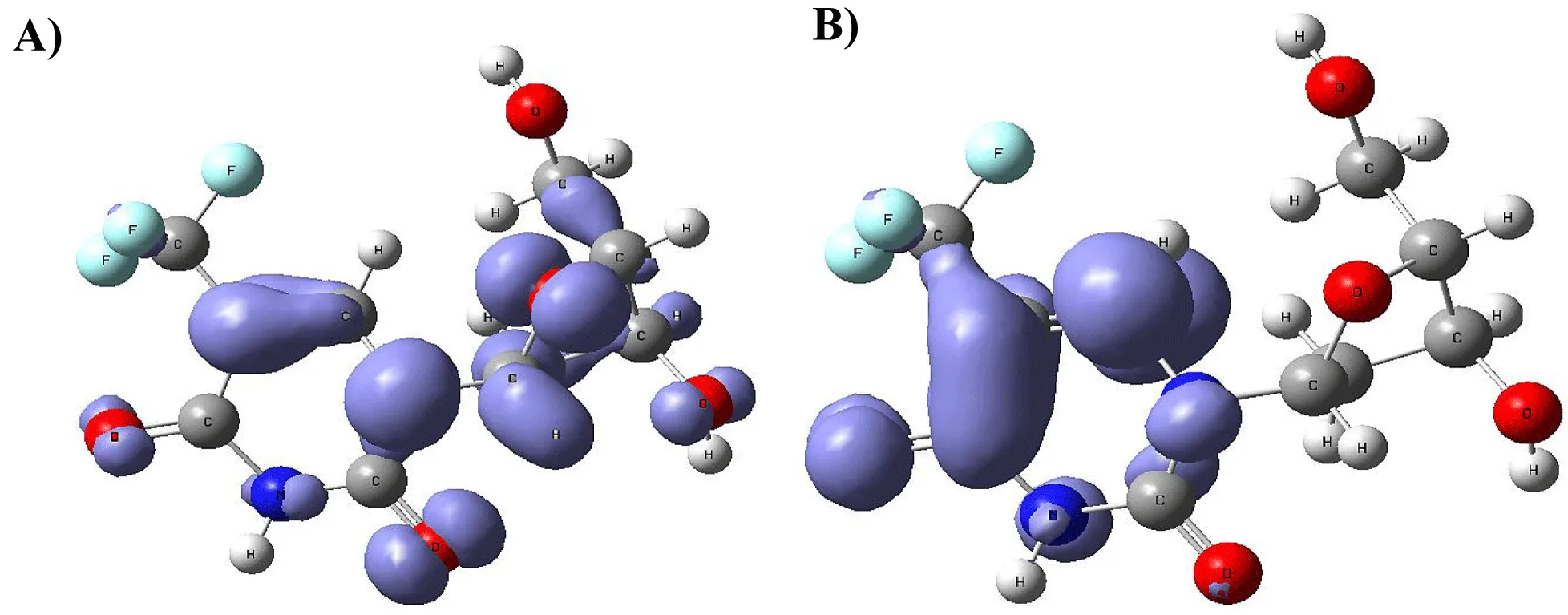
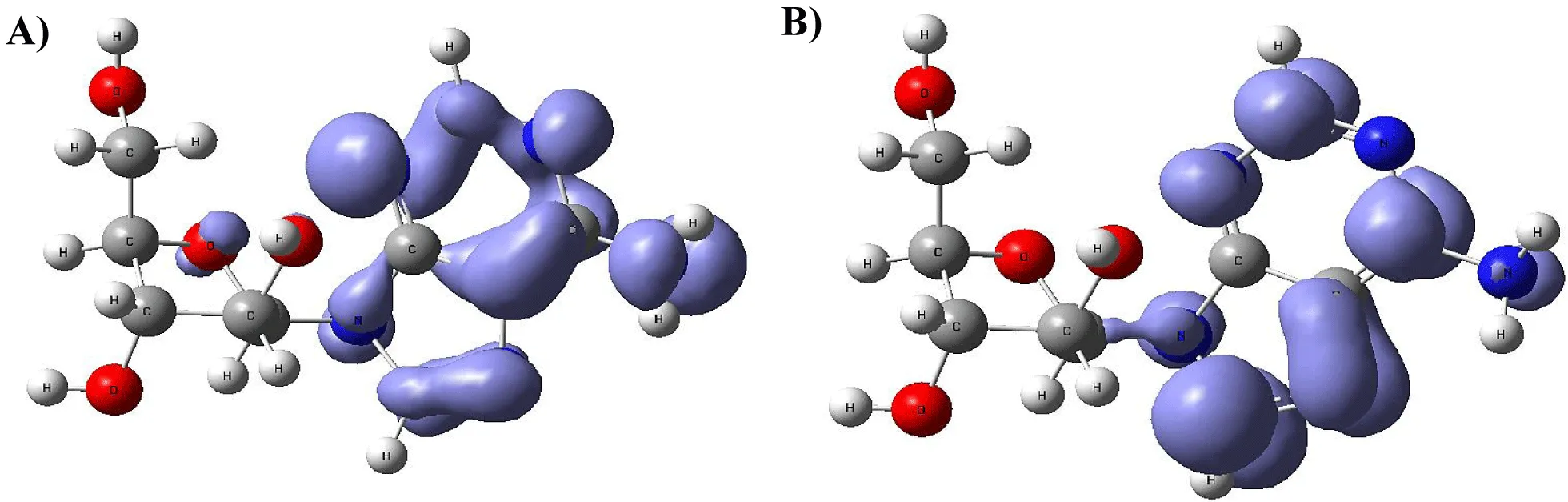
Figure 9-15 shows the Fukui Functions related to the selected compounds, considering their biological activity. Given that the reactivity indices related to electrostatic properties influence the strength of electrostatic interactions between ligands and proteins, understanding these indices helps assess the role of electrostatic forces in ligand stabilization within the protein binding site.
The central skeleton of aromaticity contains the site of local chemical reactivity for the ligand Arbidol. Aromaticity, a key concept in organic chemistry, plays a significant role in local reactivity. Aromatic systems found in molecules produce their special stability pattern and response behavior. Benzene rings demonstrate exceptional stability because π electrons spread throughout the molecule through resonance delocalization. The stability of aromatic systems affects the local reactivity by influencing the likelihood of chemical reactions occurring in their vicinity.
Aromatic systems exhibit a high electron density above and below the plane of the ring. This localized electron density affects the local reactivity by influencing the aromatic system's susceptibility to nucleophiles or electrophiles.
The Fukui functions reported can identify nucleophilic and electrophilic sites in a ligand. Ligands with nucleophilic sites may form favorable interactions with electrophilic residues in the protein and vice versa, contributing to ligand stabilization. Fukui functions can guide the design of ligands with electronic properties compatible with the protein's binding site.
Ligands tailored to interact favorably with the electronic environment of the protein binding site are more likely to achieve stable binding. Fukui functions to aid in optimizing ligand design for enhanced reactivity and stability. Developing ligands through electronic reactivity analysis allows scientists to design molecules that best suit protein electronic environments. The Fukui functions deliver important electronic reactivity data about ligands to help researchers analyze their interactions with proteins. Using Fukui functions in ligand design supports the logical creation of durable ligand-protein complexes with preferred characteristics for drug development studies and molecular recognition research.
Conclusion
Scientists face multiple hurdles while developing COVID-19 drugs due to genetic variations, the virus's quick spread, the absence of existing treatments, the complicated viral replication process, and drug safety issues. This study obtained insights into a series of ligands based on the crystal structure of SARS-CoV-2 RNA-dependent RNA polymerase (PDB code 6 m 71). Molecular docking outcomes revealed interactions with specific residues for each ligand. The back pocket protein interactions remain vital because they influence how the protein functions, shapes itself and contributes to viral replication. The stabilization mechanism of COVID-19 protein structures depends heavily on hydrogen bonding, leading to proper protein folding, stability maintenance, and functional conformational changes.
Quantum similarity analysis showed low structural ligand similarity while demonstrating high electronic similarity patterns as key elements in drug development for their influence on drug-target binding and safety levels. Combining chemical reactivity indices enhanced knowledge about ligand-protein interactions, accelerating the development of helpful drug candidates. The study focused on local reactivity aspects, especially those controlled by aromatic characteristics, to show why aromatic systems play an essential role in ligand stability and reactivity. Fukui function analysis, which identified electrophilic and nucleophilic sites within ligands, provided valuable guidance on ligand stability for binding purposes. Developing new drugs to combat COVID-19 requires complete knowledge of how ligands interact with proteins, their electronic properties, and chemical reactivity. The acquired knowledge proves vital for both therapeutic strategy improvement and the development of effective antiviral medications.
Underlying Data
Morales-Bayuelo, Alejandro, 2023, "Replication data for Study of a series of ligands used as inhibitors of the SARS-CoV-2 virus", https://doi.org/10.7910/DVN/7KFPUT, Harvard Dataverse, V1
Acknowledgment
AMB thanks to the Universidad del Sinú, Seccional Cartagena.
Funding
UNISINU-2024-I.
Conflicts of Interest/Competing Interests
The authors declare no conflict of interest.
Availability of Data and Material
Support information is not attached.
Code Availability
Institutionally licensed programs for Gaussian 09.
Authors' Contributions
AMB conceived and designed the study, conducted research, provided materials, and collected and organized data.
AMB analyzed and interpreted data.
AMB wrote the initial and final draft of the article, and provided logistic support.
ZZ and PM reviewed the final draft.
All authors have critically reviewed and approved the final draft and are responsible for the content and similarity index of the manuscript.
References
- COVID-19 consulted. 2023.
- Banerjee A, Kulcsar K, Misra V, Frieman M, Mossman K. Bats and Coronaviruses. Viruses. 2019 Jan 9;11(1):41. doi: 10.3390/v11010041. PMID: 30634396; PMCID: PMC6356540.
- Yang D, Leibowitz JL. The structure and functions of coronavirus genomic 3' and 5' ends. Virus Res. 2015 Aug 3;206:120-33. doi: 10.1016/j.virusres.2015.02.025. Epub 2015 Feb 28. PMID: 25736566; PMCID: PMC4476908.
- Song Z, Xu Y, Bao L, Zhang L, Yu P, Qu Y, Zhu H, Zhao W, Han Y, Qin C. From SARS to MERS, Thrusting Coronaviruses into the Spotlight. Viruses. 2019 Jan 14;11(1):59. doi: 10.3390/v11010059. PMID: 30646565; PMCID: PMC6357155.
- a) Graham RL, Donaldson EF, Baric RS. A decade after SARS: strategies for controlling emerging coronaviruses. Nat Rev Microbiol. 2013 Dec;11(12):836-48. doi: 10.1038/nrmicro3143. Epub 2013 Nov 11. PMID: 24217413; PMCID: PMC5147543. b) Morales-Bayuelo A, Sánchez-Márquez J. Receptor-Based Pharmacophore Modelling of a series of ligands used as inhibitors of the SARS-CoV-2 virus by complementary theoretical approaches, molecular docking, and reactivity descriptors. F1000Res. 2023 Jun 26;12:749. doi: 10.12688/f1000research.133426.1. PMID: 39291142; PMCID: PMC11406136.
- Burley SK, Berman HM, Bhikadiya C, Bi C, Chen L, Di Costanzo L, Christie C, Dalenberg K, Duarte JM, Dutta S, Feng Z, Ghosh S, Goodsell DS, Green RK, Guranovic V, Guzenko D, Hudson BP, Kalro T, Liang Y, Lowe R, Namkoong H, Peisach E, Periskova I, Prlic A, Randle C, Rose A, Rose P, Sala R, Sekharan M, Shao C, Tan L, Tao YP, Valasatava Y, Voigt M, Westbrook J, Woo J, Yang H, Young J, Zhuravleva M, Zardecki C. RCSB Protein Data Bank: biological macromolecular structures enabling research and education in fundamental biology, biomedicine, biotechnology and energy. Nucleic Acids Res. 2019 Jan 8;47(D1):D464-D474. doi: 10.1093/nar/gky1004. PMID: 30357411; PMCID: PMC6324064.
- Halgren JJ. Klicic DT. Mainz MP. Repasky EH, Knoll M, Shelley JK, Perry DE, Shaw P, Francis PS, Shenkin. Glide: A new approach for rapid, accurate docking and scor- ing. 1. Method and assessment of docking accuracy. J Med Chem. 2025;47(7):1739-49. doi: 10.1021/jm0306430.
- Friesner RA, Banks JL, Murphy RB, Halgren TA, Klicic JJ, Mainz DT, Repasky MP, Knoll EH, Shelley M, Perry JK, Shaw DE, Francis P, Shenkin PS. Glide: a new approach for rapid, accurate docking and scoring. 1. Method and assessment of docking accuracy. J Med Chem. 2004 Mar 25;47(7):1739-49. doi: 10.1021/jm0306430. PMID: 15027865.
- Sastry GM, Adzhigirey M, Day T, Annabhimoju R, Sherman W. Protein and ligand preparation: parameters, protocols, and influence on virtual screening enrichments. J Comput Aided Mol Des. 2013 Mar;27(3):221-34. doi: 10.1007/s10822-013-9644-8. Epub 2013 Apr 12. PMID: 23579614.
- Jorgensen WL, Maxwell DS, Tirado-Rives J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J Am Chem Soc. 1996;118:11225-11236. doi: 10.1021/ ja9621760.
- (a) Carbó-Dorca R, Amat L, Besalú E, Lobato M. Quantum similarity. Adv Molec Simil. 1998.
- (b) Carbó-Dorca R, Besalú E. A general survey of molecular quantum similarity huzinaga symposium, fukuoka. J Molec Struct Theochem. 1998.
- (c) Solá M, Mestres J, Carbó R, Duran M. A Comparative analysis by means of quantum molecular similarity measures of density distributions derived from conventional ab initio and density functional methods. J Chem Phys. 1996. doi: 10.1063/1.470859.
- (d) Carbó R, Besalú E. Theoretical foundation of quantum similarity in "molecular similarity and reactivity: From quantum chemical to phenomenological approaches. In: Carbó R Editor. Understanding chemical reactivity. Kluwer Academic Publishers (Amsterdam). 1995.
- (a) Morales-Bayuelo A, Matute RA, Caballero J. J Mol Mod. 2015.
- (b) Morales-Bayuelo A, Vivas-Reyes R. J Quant Chem. 2014.
- (c) Morales-Bayuelo A, Vivas-Reyes R. J Math Chem. 2013.
- (d) Morales-Bayuelo A, Valdiris V, Vivas-Reyes R. J Theor. Chem. 2014.
- (e) Morales-Bayuelo A, Torres J, Baldiris R, Vivas-Reyes R. Int J Quant Chem. 2012. doi: 10.1002/qua.23288.
- (f) Morales-Bayuelo A, Torres J, Vivas-Reyes R. Int J Quant Chem. 2012. doi: 10.1002/qua.23284.
- (g) Morales-Bayuelo A, Baldiris R, Vivas-Reyes R. J Theor Chem. 2013. doi: 10.1155/2014/239845.
- Te Velde G, Velde G te, Bickelhaupt FM, Baerends EJ, Fonseca Guerra C, a van Gisbergen SJ, Snijders JG, Ziegler T, J Comput Chem. 2001.
- Van lenthe E. J Chem. 1994.
- Perdew JP, Wang Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys Rev B Condens Matter. 1992 Jun 15;45(23):13244-13249. doi: 10.1103/physrevb.45.13244. PMID: 10001404.
- Pye CC, Ziegler T, van Lenthe E, Louwen JN. An implementation of the conductor-like screening model of solvation within the Amsterdam density functional package — Part II. COSMO for real solvents. Can. J Chem. doi: 10.1139/V09-008. 2009.
- Schipper PRT, Gritsenko OV, van Gisbergen SJA, Baerends EJ. Molecular calculations of excitation energies and (hyper)polarizabilities with a statistical average of orbital model exchange-correlation potentials. J Chem Phys. doi: 10.1063/1.480688. 2000.
- Carbó-Dorca R, Leyda L, Arnau M. How similar is a molecule to another? An electron density measure of similarity between two molecular structures. Int J Quantum Chem. doi: 10.1002/qua.560170612. 1980.
- Carbó-Dorca R, Gironés X. Int J Quant Chem. 2005.
- Bultinck P, Gironés X, Carbó-Dorca R. Reviews in computational chemistry, volume 21. Rev Comput Chem. 2005.
- Constans P, Amat L, Carbó-Dorca R. J Comput Chem. 1997.
- Carbó-Dorca R, Mercado LD. Quantum similarity and discrete representation of molecular sets. J Com Chem. 2010.
- Gironés X, Carbó-Dorca R, QSAR Combinator. Sci. 2006.
- Carbó-Dorca R, Besalú E, Mercado LD, J Com Chem. 2011.
- Carbó-Dorca R, Gironés X, Int J Quantum Chem. 2005.
- Carbó-Dorca R, Besalú E, J Comp Chem. 2010.
- Morales-Bayuelo A, Ayazo H, Vivas-Reyes R. Europ J Med Chem. 2010.
- Morales-Bayuelo A, Torres J, Vivas-Reyes R. Quantum molecular similarity analysis and quantitative definition of catecholamines with respect to biogenic monoamines associated: Scale alpha and beta of quantitative convergence. Int J Quant Chem. doi: 10.1002/qua.23284. 2012.
- Morales-Bayuelo A, Torres J, R. Baldiris R, Vivas-Reyes R. Quantum molecular similarity analysis and quantitative definition of catecholamines with respect to biogenic monoamines associated: Scale alpha and beta of quantitative convergence. Int J Quant Chem. 2012. doi: 10.1002/qua.23284.
- Morales-Bayuelo A, Torres J, Vivas-Reyes R. Hückel treatment of pyrrole and pentalene as a function of cyclopentadienyl using Local Quantum Similarity Index (LQSI) and the Topo-Geometrical Superposition Approach (TGSA). doi: 10.1142/S0219633612500150. J Theo Comp Chem. 2012.
- Morales-Bayuelo A, Vivas-Reyes R. Topological model to quantify the global reactivity indexes as local in Diels–Alder reactions, using Density Function Theory (DFT) and Local Quantum Similarity (LQS). J Math Chem. doi: 10.1007/s10910-012-0069-8. 2013.
- Morales-Bayuelo A, R Baldiris, Vivas-Reyes R. J Theor Chem. 2013.
- Morales-Bayuelo A, Vivas-Reyes R. J Quant Chem. 2014.
- Morales-Bayuelo A, V Valdiris, Vivas-Reyes R. J Theor Chem. 2014
- Morales-Bayuelo A, Vivas-Reyes R. Theoretical calculations and modeling for the molecular polarization of furan and thiophene under the action of an electric field using quantum similarity. J Quant Chem. 2014. doi : 10.1155/2014/585394.
- Parr RG, Pearson RG. Absolute hardness: Companion parameter to absolute electronegativity. J Am Chem Soc. 1983;105(26). doi: 10.1021/ja00364a005.
- Geerlings P, De Proft F, Langenaeker W. Conceptual density functional theory. Chem Rev. 2003 May;103(5):1793-873. doi: 10.1021/cr990029p. PMID: 12744694.
- Chattaraj PK, Sarkar U, Roy DR. Electrophilicity index. Chem Rev. 2006 Jun;106(6):2065-91. doi: 10.1021/cr040109f. PMID: 16771443.
- Parr RG, Szentpaly Lv, Liu S. Electrophilicity Index. J Am Chem Soc. 1999;121(9). doi: 10.1021/ja983494x.
- Galván M, Pérez P, Contreras R, Fuentealba P. A direct evaluation of regional Fukui functions in molecules. Chem Phys Lett. 1999;304(5-6):405-413. doi: 10.1016/S0009-2614(99)00325-5.
- Yang W, Mortier WJ. The use of global and local molecular parameters for the analysis of the gas-phase basicity of amines. J Am Chem Soc. 1986 Sep 1;108(19):5708-11. doi: 10.1021/ja00279a008. PMID: 22175316.
- Fuentealba P, Pérez P, Contreras R. Higher order derivatives for nuclear indexes in the framework of density functional theory. J Chem Phys. 2000;115:6822-6826. doi: 10.1063/1.1394755.
- 43. Y 45. Y Zhao, DG Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, non-covalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc. 2008;120:215. doi: 10.1007/s00214-007-0310-x.
- MJ Frisch, GW Trucks, HB Schlegel, GE Scuseria, MA Robb, JR Cheeseman, G Scalmani, V Barone, B Mennucci, GA Petersson, H Nakatsuji, M Caricato, X Li, HP Hratchian, AF Izmaylov, J Bloino, G Zheng, JL Sonnenberg, M Hada, M Ehara, K Toyota, R Fukuda, J Hasegawa, M Ishida, T Nakajima, Y Honda, O Kitao, H Nakai, T Vreven, JA Montgomery, JE Peralta, F Ogliaro, M Bearpark, JJ Heyd, E Brothers, KN Kudin, VN Staroverov, R Kobayashi, J Normand, K Raghavachari, A Rendell, JC Burant, SS Iyengar, J Tomasi, M Cossi, N Rega, JM Millam, M Klene, JE Knox, JB Cross, V Bakken, C Adamo, J Jaramillo, R Gomperts, RE Stratmann, O Yazyev, AJ Austin, R Cammi, C Pomelli, JW Ochterski, RL Martin, K Morokuma, VG Zakrzewski, GA Voth, P Salvador, JJ Dannenberg, S Dapprich, AD Daniels, O Farkas, JB Foresman, JV Ortiz, J Cioslowski, DJ Fox. Spectroscopic Evaluation of the Molecular Structures of di-µ-Chlorobis(1,5-Cyclooctadiene) Iridium (I) and Rhodium (I) Complexes. Gaussian Inc. Wallingford CT; 2009.
Content Alerts
SignUp to our
Content alerts.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.