Heterodyne Light Source Using Two Tandem Acousto-Optic Modulators under Bragg Diffraction Conditions

We propose a novel heterodyne light source architecture employing two tandem Acousto-Optic Modulators (AOM) operating under Bragg-diffraction conditions. A mirror and a half-wave plate are strategically positioned between the AOMs. By fine-tuning the angle of the mirror relative to the AOMs, only the +1st- or −1st-order light is generated, allowing the two light beams to coincide. The beat frequency is determined by the difference in modulation frequencies. In order to demonstrate the feasibility of this architecture, we use this light source in Common-Path Heterodyne Interferometry (CPHI) to measure the gold film thickness of a Surface Plasmon Resonance (SPR) sensor. The experimental results are in good agreement with the outcomes of mathematical simulations. In addition, the heterodyne light source has two linear polarizations perpendicular to each other with a frequency difference of 10 kHz, and the utilization rate of the light source can reach 90%.

Heterodyne light sources commonly used in research include Zeeman lasers [1,2], Mach–Zehnder architectures [3,4] and Electro-Optic Modulator (EOM) architecture [5]. Among these, the Zeeman laser functions as a self-contained heterodyne light source, offering a high beat frequency but at a high cost. The heterodyne light source based on the Mach–Zehnder architecture consists of two Acousto-Optic Modulators (AOM); however, as it lacks a common-path architecture, it is susceptible to environmental disturbances. Additionally, the architecture only uses +1st order light or -1st order light, the 0th order light is almost wasted, so the utilization rate of the laser is low. The heterodyne light source based on the EOM architecture requires full-wave voltage modulation, which causes a temperature rise in the electro-optic crystal, potentially leading to phase errors due to the high voltage.

Recently, Chiu MH, et al. [6] proposed a heterodyne light source using two AOMs connected in series. While this setup is simple to implement, the diffraction efficiency remains suboptimal because the modulators are operated under Raman-Nath conditions. The disadvantage of this architecture is that it will also lose a part of the 0th order light, although the contrast of interference is also high, but the utilization rate of the laser is low. In order to improve its shortcomings, we propose an optimized configuration with two AOMs connected in series, both operating under Bragg-diffraction conditions. When Bragg diffraction is generated, it is not a vertical incidence, but an oblique incidence, so the conditions are different from those of Raman-Nath diffraction. Through fine-tuning of the mirror and the two AOMs to ensure that the two orthogonally polarized light beams coincide, the heterodyne interference signal is substantially enhanced and the utilization rate of the laser approaches 90%.

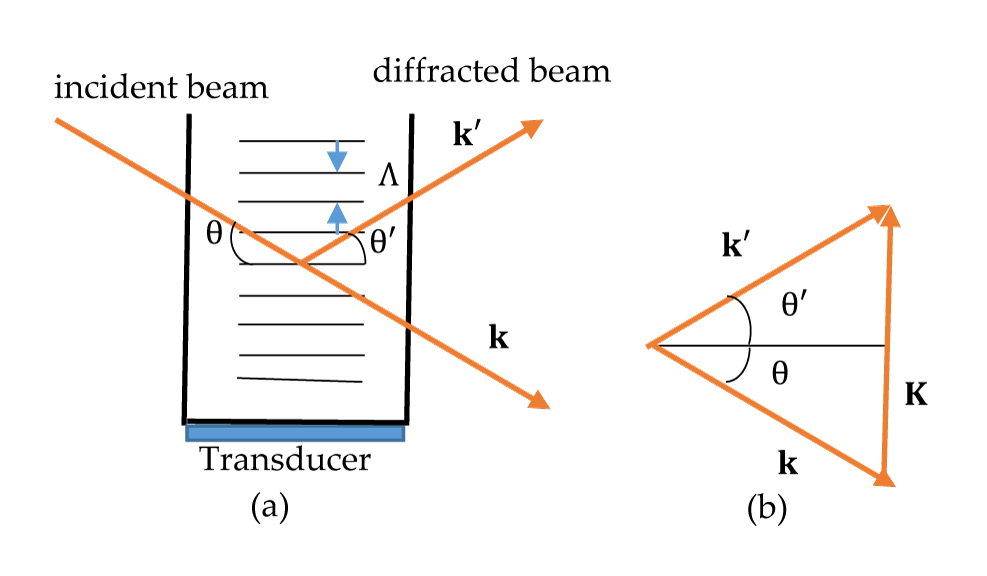
In the acousto-optic modulator (AOM) shown in figure 1(a), the Bragg diffraction conditions are derived from the triangle in figure 1(b) and are expressed as [7]:

Figure 1: The +1st-order diffraction beam in Acousto-Optic Modulator (AOM) under the Bragg diffraction condition.

$\begin{array}{l}\text{then K}={\text{k}}^{\text{'}}\text{sin}{\theta }^{\text{'}}+\text{ksin}\theta .If\theta \text{'}\approx \theta \text{ and }\\ {\text{k}}^{\text{'}}\approx \text{k}=\frac{2\pi }{\lambda },then\text{ K}=\frac{2\pi }{\Lambda }=2\text{ksin}\theta \text{ and:}\end{array}$

${\text{k}}^{\text{'}}=\text{k}+\text{K (1)}$

$\Lambda =\frac{\lambda }{2sin\theta }=\frac{v_s}{f_s}\text{ (2)}$

where K, k', and are the wave vectors of the sound wave, diffracted beam, and incident beam, respectively, while θ and θ' are the incident and diffracted angles, respectively. Here, v_s is the sound velocity, f_s is the frequency of the sound wave or the modulation frequency, Λ is the wavelength of sound, and λ is the wavelength of the beam in the medium. If the frequency of the incident beam is f = f₀, then the Doppler effect causes the frequency of the diffracted beam to be f' = f₀ - fs, where the beam is the +1st-order beam. Eq. (2) represents the Bragg condition.

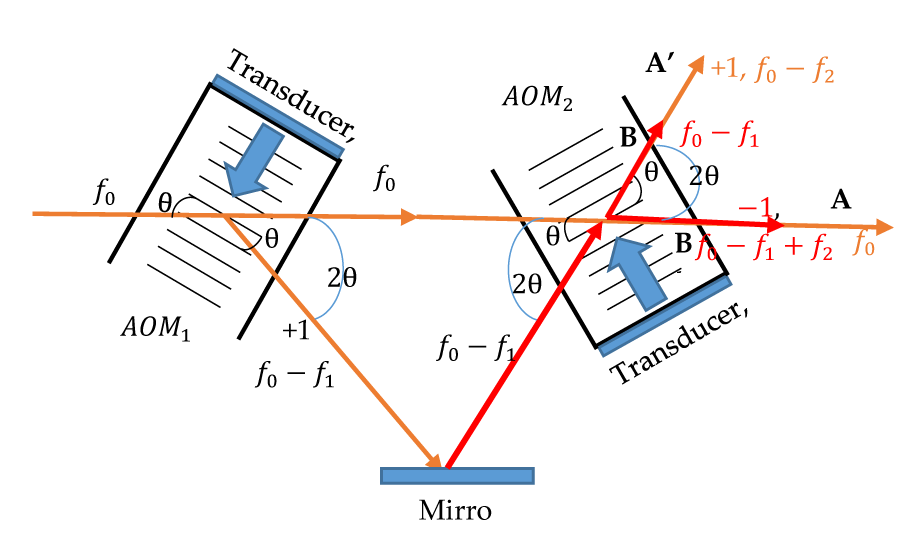
The basic optical setup of the heterodyne light source is shown in figure 2 to further illustrate the principle of the coincidence of the two beams produced by the two AOMs connected in series. Here the modulation frequencies of AOM₁ and AOM₂ are f₁ and f₂, respectively. Under Bragg diffraction conditions, if the optical frequency of the laser light is f₀, then the optical frequency of the 0th-order beam from AOM₁ is unchanged at f₀, while the optical frequency of the +1st-order beam is f₀ − f₁. The angle between these two beams is 2θ. The 0th-order beam from AOM₁ is incident on the second AOM (AOM₂). The optical frequency of the direct beam remains unchanged at f₀ which is denoted as beam A, while the optical frequency of the +1st-order beam is f₀ − f₂ and is denoted as beam A'. The angle between these two beams is 2θ. In addition, the diffracted light with a frequency of f₀ − f₁ is reflected into AOM₂ after passing through mirror M. The direct light frequency remains f₀ − f₁, denoted as beam B, and its −1st-order beam has a frequency of f₀ − f₁ + f₂, denoted as beam B'. By fine-tuning the angle of mirror M so that the angle of incidence is θ (that is, the angle between the 0th-order beams is 2θ), the two sets of beams can coincide. One set consists of beam A' coincident with beam B, while the other set consists of beam A coincident with beam B'. The frequency difference between the two beams in both sets is f = | f₂ - f₁ |.

Figure 2: The basic optical setup of a heterodyne light source.

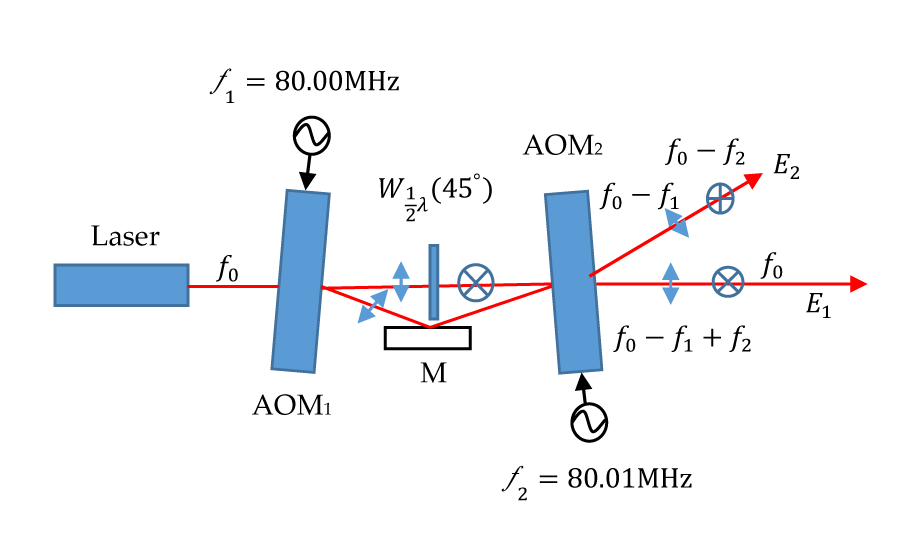
As illustrated in figure 3, the proposed heterodyne light source consists of a laser, two AOMs (AOM₁, AOM₂), a Mirror (M), and a half-wave plate W_λ⁄2 (45°) positioned at an azimuth angle of 45°.

Figure 3: Schematic of the heterodyne light source utilizing two tandem AOMs in Bragg-diffraction conditions. Components: helium-neon laser (λ = 632.8 nm); AOM₁, AOM₂: acousto-optic modulators; W_λ⁄2 45°: half-wave plate; M: mirror.

The acoustic waves of the two AOMs propagate in opposite directions. In this configuration, the laser operates at a frequency of f₀, and the modulation frequencies of AOM₁ and AOM₂ are set to f₁ (80.00 MHz) and f₂ (80.01 MHz), respectively. Fine-tuning the AOMs enables them to operate under Bragg-diffraction conditions, the diffraction efficiency of the ±1st-order light reaches approximately 44%, while the 0th-order light achieves approximately 51% efficiency. When the 0th-order light from AOM₁, which is p-polarized, passes through the half-wave plate W_λ⁄2 (45°), the outgoing light becomes s-polarized, making its polarization perpendicular to that of the +1st-order light. The +1st-order light from AOM₁, after being reflected by mirror M, is directed into AOM₂. Upon passing through AOM₂, the frequencies of the 0th- and −1st-order light beams become f₀ − f₁ and f₀ − f₁ + f₂, respectively. In addition, after the 0th-order light of AOM₁ passes through AOM₂, the frequencies of the 0th- and +1st-order lights from AOM₂ are f₀ and f₀ − f₂, respectively, as illustrated in figure 3. By adjusting the angle of mirror M relative to the AOMs, the 0th-order p-polarized light (f₀ − f₁) coincides with the +1st-order s-polarized light (f₀ − f₂), while the −1st-order p-polarized light (f₀ − f₁ + f₂) coincides with the 0th-order s-polarized light (f₀). The Jones vectors of the electric field intensities E₁ and E₂ can be expressed as:

$E_1=\left[\begin{array}{c}{A}_{x1}{e}^{j2\pi \left(f_0-f_1+f_2\right)t}\\ A_{y1}{e}^{j2\pi f_{0}t}\end{array}\right]\text{ (3)}$

$E_2=\left[\begin{array}{c}{A}_{x2}{e}^{j2\pi \left(f_0-f_1\right)t}\\ A_{y2}{e}^{j2\pi (f_0-f_{2}t}\end{array}\right]\text{ (4)}$

Respectively, where A_x1 and A_y1 are the amplitudes of the electric field E₁ in the x and y directions, and A_x2 and A_y2 are the amplitudes of the electric field E₂ in the x and y directions, respectively. Once the two orthogonally polarized light beams coincide, two sets of heterodyne light sources are formed, with a frequency difference of f = | f ₂ - f ₁| = 10 kHz.

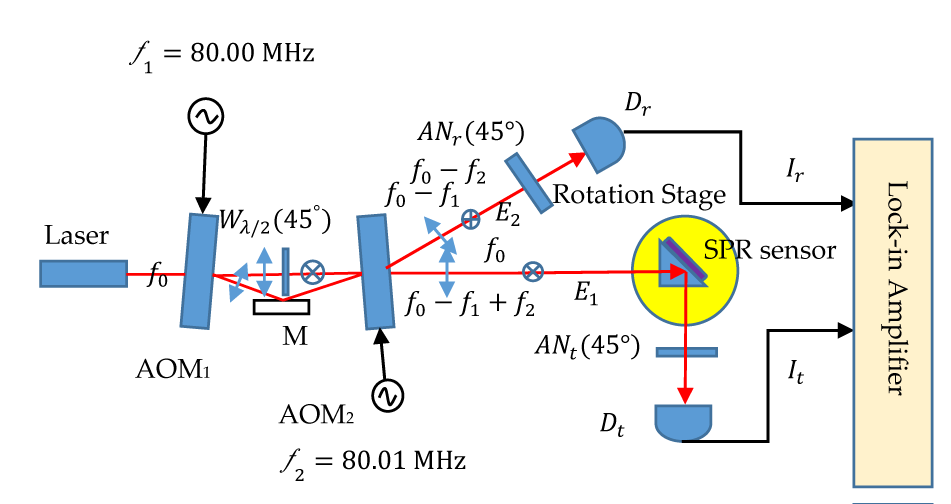
In order to demonstrate the feasibility of the proposed heterodyne light-source architecture, we use common-path heterodyne interferometry to measure the thickness of the gold film of a known Surface Plasmon Resonance (SPR) sensor. The experimental architecture is illustrated in figure 4.

Figure 4: Verification experiment: A common-path heterodyne interferometer based on the proposed heterodyne light-source architecture used for measuring the gold-film thickness of the SPR sensor. AN_r, AN_t: analyzers; D_r, D_t: photodetectors; SPR: SPR sensor; SR830: lock-in amplifier.

We use an analyzer with a transmission axis set at a 45° angle to allow the orthogonal polarized light beams to interfere. The resulting interference signal was detected by a photodetector. The reference signal detected by is expressed as

$I_r=I_{r0}\left(1+V_{r}cos\left(2\pi ft\right)\right)\text{ (5)}$

and the test signal detected by D_t can be expressed as:

$I_t=I_{t0}\left(1+V_{t}cos\left(2\pi ft+\varphi \right)\right)\text{ (6)}$

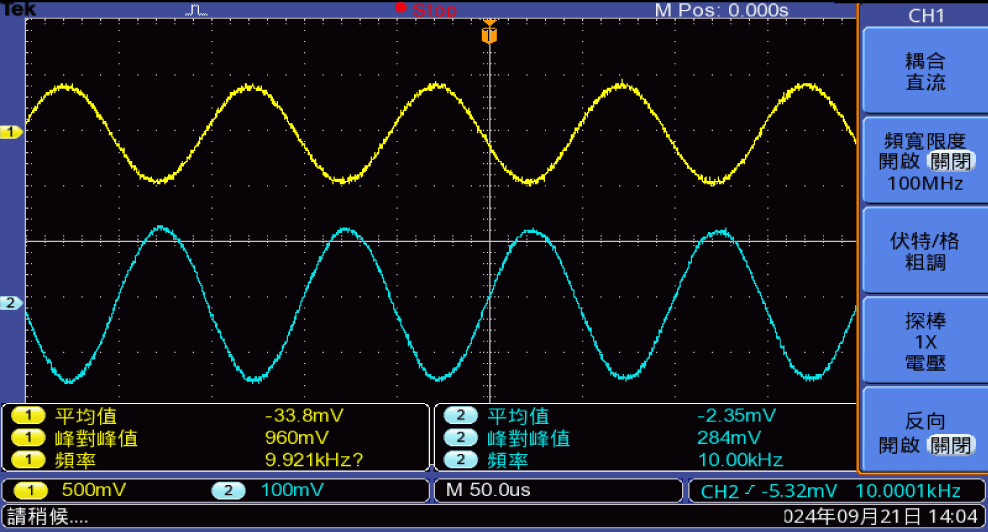
where I_r0 and I_t0 are the average intensities, V_r and V_t are the visibilities, and ϕ is the phase-shift difference of the SPR sensor. The interference signals were recorded using an oscilloscope, as shown in figure 5. According to the principle of the SPR sensor, the phase shift difference ϕ can be expressed as:

Figure 5: Wave forms of the test and reference signals. The frequency of two signals is 10kHz.

$\varphi ={\delta }_p-{\delta }_s\text{ (7)}$

where δp and δs are the phase shifts of the p- and s-polarized light beams after passing through the SPR sensor.

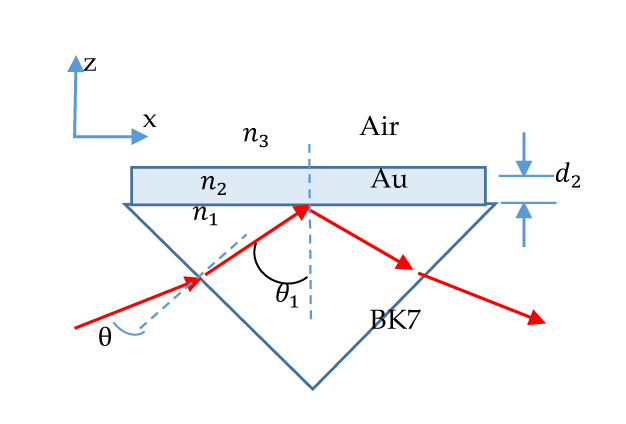
As illustrated in figure 6, the refractive indices of the prism (BK7), Au, and air are denoted by n₁, n₂ and n₃, respectively.

Figure 6: Configuration of SPR sensor.

The total reflection coefficient of the p- or s-polarized light can be expressed as [8]:

$r_{123}^t=\frac{r_{12}^t+r_{23}^t{e}^{i2k_{z2}{d}_2}}{1+r_{12}^t{r}_{23}^t{e}^{i2k_{z2}{d}_2}}=\left|r_{123}^t\right|\angle {\delta }_t,t=pors\text{ (8)}$

where d2 is the thickness of Au and:

$k_{z2}{d}_2=k_0{n}_2{d}_{2}cos{\theta }_2=\raisebox{1ex}{$2\pi d_2$}\!\left/ \!\raisebox{-1ex}{${\lambda }_0$}\right.{\left(n_2^2-n_1^{2}si{n}^2{\theta }_1\right)}^{1/2},\text{ (9)}$

where n₂ and n₁ are the refractive indices of Au and the prism, respectively; θ₂ and θ₁ are the angles of the light beams at the Au–prism interface;

$r_{ij}^t=\frac{E_i^t-E_j^t}{E_i^t+E_j^t}, (t=s or p)$

is the reflection coefficient at the boundary between mediums i and j,

where; $E_{i(j)}^p=\raisebox{1ex}{$n_{i(j)}{}^2$}\!\left/ \!\raisebox{-1ex}{$k_{zi(j)}$}\right.E_{i(j)}^s=k_{zi(j)}$ ;

and i, j = 1,2,3 For a laser wavelength of 632.8 nm, the refractive indices of the BK7 prism, Au, and air are 1.51509, (−12 + 1.26i)^1/2, and 1.0003, respectively. Substituting these values into Eqs. (7)–(9) yields the total reflection coefficient and the phase shift difference ϕ. The resonance angle is near at for the boundary between Au and Bk7 and surface plasmon resonance conditions must be met

$k_{sp}=\sqrt{\frac{{\epsilon }_1{\epsilon }_2}{{\epsilon }_1+{\epsilon }_2}}{k}_0\text{ (10)}$

where ε2 and ε1 are the relative permittivity of Au and the Bk7 prism, respectively and k₀ is the wavenumber in vacuum.

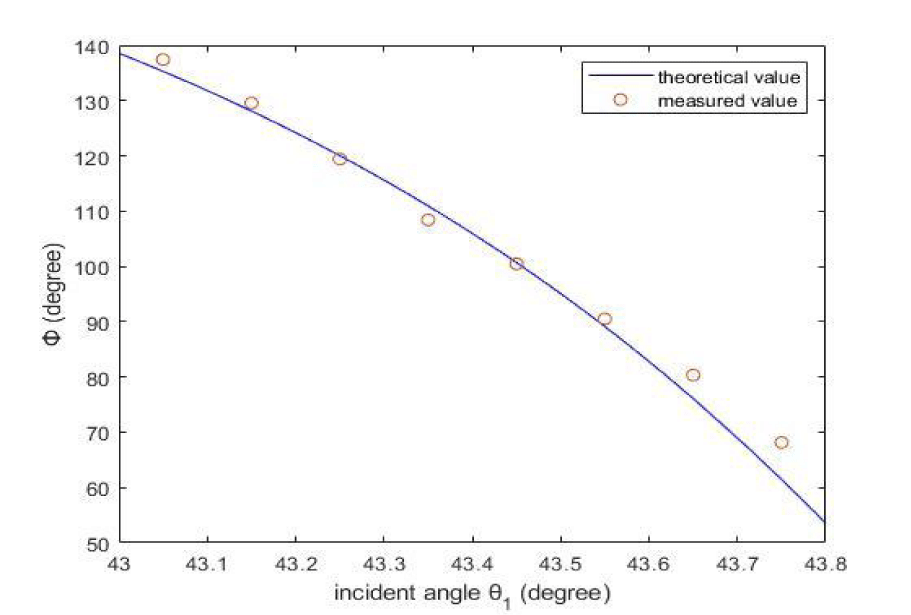
By rotating the SPR sensor counterclockwise near the resonance angle (from 43o to 48o), the phase-shift difference ϕ and the angle of incidence θ₁ were recorded. The experimental data, denoted by red circles, are shown in figure 7, alongside simulation results (solid line) generated using MATLAB. The optimal gold-film thickness obtained from the experiment was 35 nm, which is in good agreement with the actual gold-film thickness of the SPR sensor.

Figure 7: Experimental results for the SPR’s gold-film thickness measurement using the common-path heterodyne interferometry (approximately 35 nm). Red circles: experimental values; blue line: simulation curve.

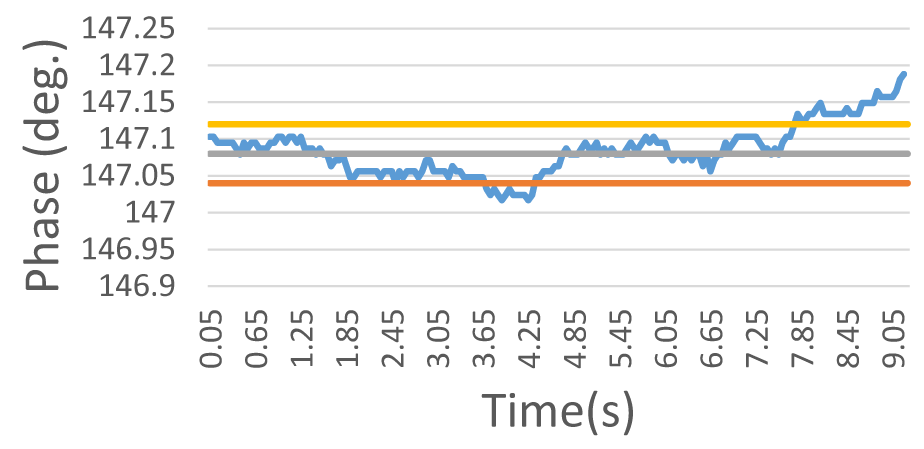
These experiments confirm the feasibility of the proposed heterodyne light source as a reliable component for a common-path heterodyne interferometer. The phase resolution determined by stander deviation test was 0.04° as shown in figure. 8. From table 1, the phase resolution of our structure is better than that of the Mach-Zehnder AOM structure and EOM architecture in our experiments. Although it is not better than Zeeman laser. But because of the low price, it still has its value. Under Bragg-diffraction conditions, the interference contrast could exceed 0.7 and the utilization rate of the light source was approximately 90%.

Figure 8: The standard deviation of phase measurement.

This heterodyne light-source architecture, featuring dual AOMs in tandem under Bragg-diffraction conditions, addresses the limitations of the Mach–Zehnder architecture regarding light-source utilization, as well as the low diffraction efficiency of previous dual-AOM architectures [6]. It offers ease of assembly and reduces the need for components such as beamsplitters, polarized beamsplitters, and an additional mirror, while only requiring the addition of a half-wave plate. This makes it a highly efficient and practical solution. Although it has a good utilization rate of light source, the long arrangement of components in the architecture is its disadvantage, so there are still improvements in the future.

Conceptualization, M.H. Chiu; methodology, M.H. Chiu; software, C.C. Chiu; formal analysis, M.H. Chiu; investigation, C.C. Chiu; resources, M.H. Chiu; data curation, C.C. Chiu; writing-original draft preparation, M.H. Chiu; writing-review and editing, M. H. Chiu; visualization, M.H. Chiu; supervision, M. H. Chiu; project administration, M.H. Chiu; funding acquisition, M.H. Chiu.

Data Availability Statement

Where no new data were created.

Funding

The current study was funded by the National Science and Technology Council (NSTC112-2221-E-150-035, Taiwan).

Acknowledgment

M.H. Chiu thanks the NSTC in Taiwan for supporting this work.

Disclosures

The authors declare no conflicts of interest.

1. AS Badger, TA Rabson. Zeeman effect and ruby laser polarization. In Proceedings of the IEEE. 1964;52(9):1047-1048. doi: 10.1109/PROC.1964.3239. doi: 10.1109/PROC.1964.3239.
2. Takasaki H, Umeda N, Tsukiji M. Stabilized transverse zeeman laser as a new light source for optical measurement. Appl Opt. 1980 Feb 1;19(3):435-41. doi: 10.1364/AO.19.000435. PMID: 20216866.
3. MJ Ehrlich, LC Philips, JW Wanger. Voltage-controlled acousto-optic phase shifter. Rev Sci Instrum. 1988;59:2390-2392. doi: 10.1063/1.1139915.
4. Gazalet MG, Ravez M, Haine F, Bruneel C, Bridoux E. Acousto-optic low-frequency shifter. Appl Opt. 1994 Mar 1;33(7):1293-8. doi: 10.1364/AO.33.001293. PMID: 20862154.
5. DC Su, MH Chiu, CD Chen. Simple two-frequency laser. Prec Eng. 1996;18:161-163. doi: 10.1016/0141-6359(96)80485-5.
6. MH Chiu, CC Chiu. Tandem heterodyne light sources with dual acousto-optic modulators as an example of the optical rotation measurement of water as a function of temperature. Appl Opt. 2024;63:6955-6959. doi: 10.1364/AO.531977.
7. A Yariv, P Yeh. Optical waves in crystals:Propagation and control of laser radiation. Wiley, John Wiley & son Inc. USA; 2003. p.329-336.
8. H Raether. Surface plasmons on smooth and rough surfaces and on gratings. Springer Tracts in Modern Physics. 1988;111.