Omicron Waves of the COVID-19 Pandemic and Efficacy of Vaccinations and Testing

The sharp increase in the number of new COVID-19 cases in late 2021 and early 2022, which occurred even in countries with high vaccination levels, has raised the question about the possibility of overcoming the pandemic only through vaccination. Averaged daily numbers of new COVID-19 cases and deaths per capita and their ratio were used to find links with the percentages of fully vaccinated people and boosters and the tests per case ratio. The datasets for European and some other countries and regions corresponding to February 01, 2022 were used. Simple linear and non-linear statistical methods showed that vaccinations can significantly reduce the likelihood of deaths and the increase in the tests per case ratio diminishes the number of infections. These conclusions are consistent with the previous study based on the data from September 01, 2021 (before the advent of the Omicron). However, the numbers of new daily Omicron cases per capita increase with the increase of the percentage of fully vaccinated people and boosters. It looks that removal of restrictions on the movement of vaccinated persons and the abolition of many quarantine restrictions have led to a sharp increase in the number of infections. To overcome the pandemic, the increase of the tests per case ratio and extension of quarantine restrictions are necessary.

To investigate the infectivity of new strains of SARS-CoV-2, effectiveness of quarantine, testing and vaccination, different relative characteristics (calculated per capita) can be used. In particular, averaged numbers of new daily cases DCC and deaths DDC per million are regularly reported by COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU) [1]. The percentages of fully Vaccinated People (VC) and Boosters (BC) and Daily Tests per Case ratios (DTC) can be also found in [1]. The daily characteristics DCC, DDC, DTC, etc. allow us to investigate the recent situation in comparison with accumulated numbers of COVID-19 Cases (CC), Death (DC) and Tests (TC) per capita [2,3].

Vaccinations and successes in vaccine logistics management can reduce the mortality caused by SARS-CoV-2 [3-7]. Nevertheless, the Omicron waves in Europe were characterized by very high DCC values [1]. This characteristic and the daily numbers of new Deaths per Capita (DDC) are very important in order to investigate the efficiency of vaccinations and testing. In particular, it was shown in [3,8] that rather high numbers of VC did not prevent new pandemic waves in the summer and autumn of 2021. In this paper we will try to update the correlations between DCC, DDC, DDC/DCC and VC values for Omicron waves (based on the JHU datasets corresponding to February 01, 2022). The rather high BC values in Europe allow finding the links between boosters and DCC, DDC, DDC/DCC values. The linear and non-linear correlations between the testing level DTC and DCC, DDC, DDC/DCC will also be investigated.

The data sets regarding the relative characteristics (per capita) reported by JHU as of February 01, 2022 [1] will be used. The figures corresponding to the version of the JHU data available on February 06, 2022 are presented in table 1. The characteristics VC, BC and DTC are taken without smoothing. Since daily characteristics DCC (new cases per million) and DDC (new deaths per million) are very random and demonstrate some weekly periodicity, the smoothed (averaged) values will be used. These values are calculated and displayed by JHU with the use of figures registered during the previous 7 days. This smoothing procedure differs from one proposed in [9-11], where the values registered in the nearest 7 days were used.

The linear regression will be used to calculate the regression coefficients r and the coefficients a and b of corresponding best fitting straight lines [12,13]:

$y=a+bx\text{ (1)}$

where x are VC, BC, DTC values and y are DCC, DDC, and DDC/DCC values.

To find links between DCC and DTC values, the following non-linear correlation will also be applied:1

$y=a+b{(x+c)}^{\gamma },a\ge o,b>o,x>-c\text{ (2)}$

at γ = 1 relationship (2) reduces to (1) and can be rewritten as follows:

$z\equiv \log \left|y-a\right|=\log (b)+\gamma \log (x+с)\text{ (3)}$

Then for new random variables z and, $w\equiv \log (x+c)$ a linear regression similar to (1) can be applied. The constant parameters γ, log(b) and corresponding best fitting lines can be found with the use of standard formulas for the linear regression for every fixed values of constant parameters a and c.

The F-test for the null hypothesis that says that the proposed linear relationships (1) or (3) fit the data sets will also be applied. The experimental values of the Fisher function can be calculated with the use of the formula:

$F=\frac{r^2(n-m)}{(1-r^2)(m-1)}\text{ (4)}$

where n is the number of observations (number of countries and regions taken for statistical analysis); m = 2 is the number of parameters in the regression equation [13]. The corresponding experimental values F have to be compared with the critical values Fc(k1,k2) of the Fisher function at a desired significance or confidence level (k₁ = m – 1, k₂ = n – m [14]). If F/F_c(k₁,k₂)<1, the null hypothesis is not supported by the results of observations. The highest values of F/F_c(k₁,k₂) correspond to the most reliable hypotheses [15]. In the case of non-linear regression (2) the values of additional parameters a and c must be chosen in order to ensure the maximum of the correlation coefficient r or the highest values of F/F_c(k₁,k₂) (similar to the parameter identification methods used in [9]).

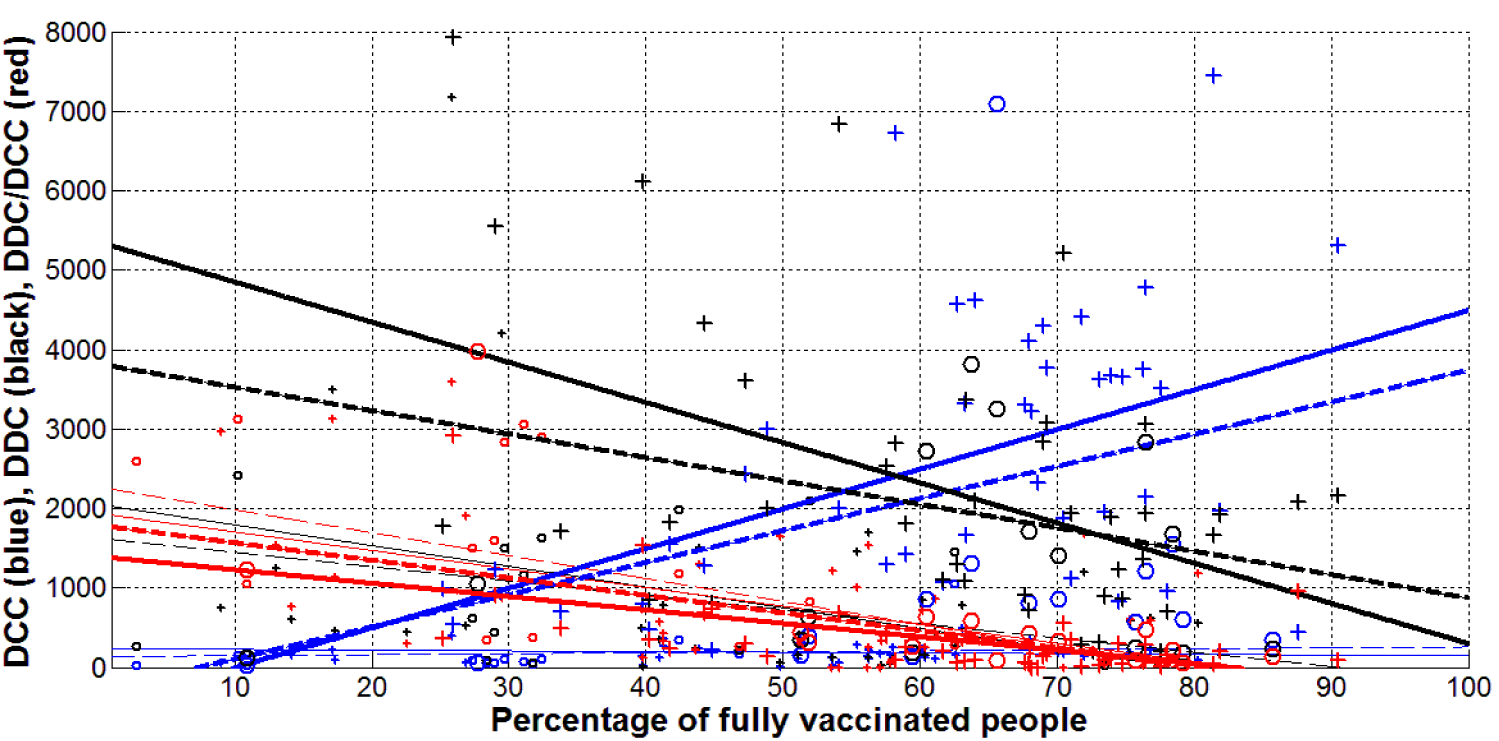
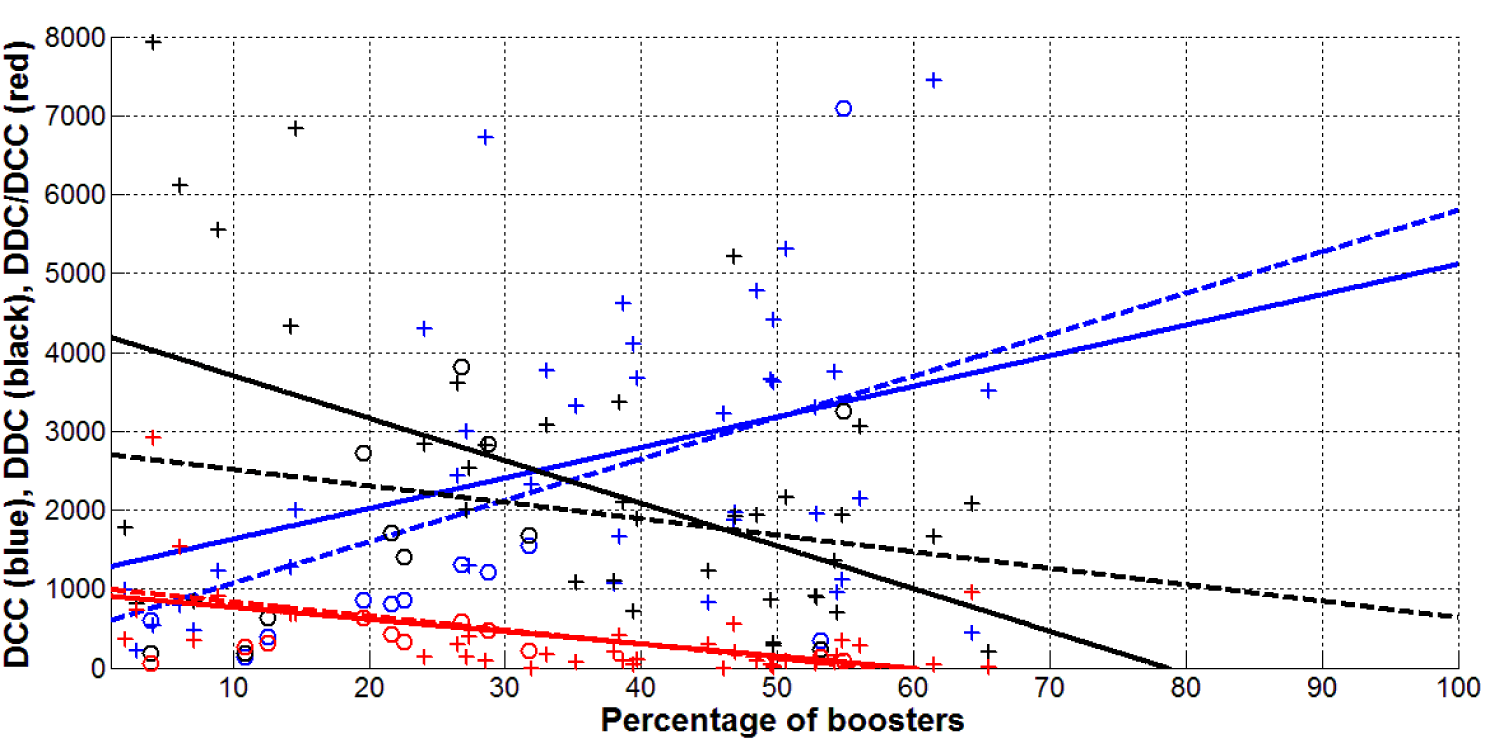
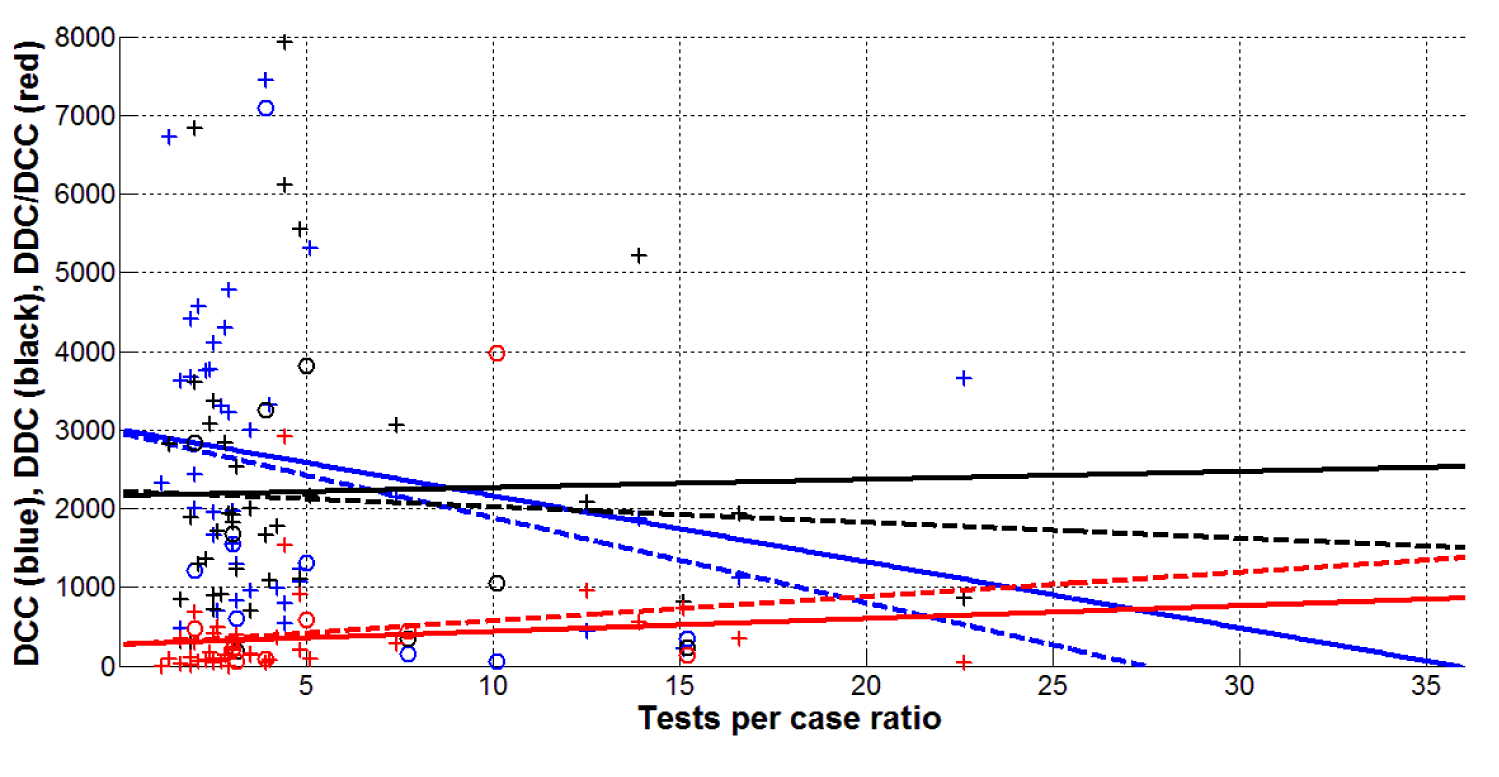
The results of the linear regression application are presented in table 2 and figures 1-3. The data sets corresponding to the European countries and complete datasets with the information about some other countries and regions listed in table 1 have been used. Thus, we have two different numbers of observations n for every application of the linear relationship (1). Due to the lack of some data, the numbers n are different for different relationships. Corresponding values of n, the regression coefficients r, coefficients a and b; values of the Fisher function F,Fc(k1,k2) and F/F_c(k₁,k₂) are listed in table 2. The best fitting lines (1), calculated with the use of corresponding values a and b are shown in figures 1-3 by solid lines for European datasets and by dashed lines for complete datasets. The DCC, DDC, and DDC/DCC values are represented by “crosses” for European countries and by “circles” for other countries and regions.

Figure 1: Smoothed daily characteristics of the COVID-19 pandemic vs. percentage of fully Vaccinated People (VC).
New cases per million (DCC, blue), new deaths per 500 million (DDC x 500, black), daily mortality rate (DDC x 105/DCC, red). Best fitting lines (1) are solid for European datasets and dashed for complete datasets. “Crosses” represent the European datasets, “circles” - figures for other countries and regions. Bold lines and large markers correspond to February 1, 2022; thin lines and small markers – to September 01, 2021, [3].

Figure 2: Smoothed daily characteristics of the COVID-19 pandemic vs. percentage of Boosters (BC) as of February 1, 2022.
New cases per million (DCC, blue), new deaths per 500 million (DDC x 500, black), daily mortality rate (DDC x 105/DCC, red). Best fitting lines (1) are solid for European datasets and dashed for complete datasets. “Crosses” represent the European datasets, “circles” - figures for other countries and regions.

Figure 3: Smoothed daily characteristics of the COVID-19 pandemic vs. tests per case ratio (DTC) as of February 01, 2022.
New cases per million (DCC, blue), new deaths per 500 million (DDC x 500, black), daily mortality rate (DDC x 105/DCC, red). Best fitting lines (1) are solid for European datasets and dashed for complete datasets. “Crosses” represent the European datasets, “circles” - figures for other countries and regions.

Table 2 and figure 1 illustrate that there are correlations between DCC, DDC, DDC/DCC values and the percentage of fully vaccinated people VC, since F/F_c(k₁,k₂)>1 for all 6 calculations (see the rows in table 2 corresponding to figure 1). The correlations were revealed for the relationships versus BC (there is only one exception for the global DDC values, see the rows in table 2 corresponding to figure 2).

As of September 01, 2021 no statistical significant correlation was revealed for the relationship DCC versus VC, [3] (Figure 1). The Omicron waves have changed the situation even more unexpectedly. As of February 01, 2022, the increase of vaccination levels (both VC and BC values) increases the numbers of new daily cases DCC (see positive values of parameter a in table 2 and bold blue lines in figures 1,2). This unexpected fact can be explained by the removal of restrictions on travel and visits to crowded places for vaccinated persons.

During the Omicron waves, the numbers of new deaths per capita are much higher than DDC values in September 2021 (compare bold and thin black lines in figure 1). This fact can be explained by a huge increase in the number of cases DCC in Omicron waves. In comparison with DCC, the DDC values always decrease with the increasing of vaccination levels VC and BC (see black lines in figures 1,2). But the forecast for Omicron waves is more pessimistic. As of September 01, 2021, the critical levels of VC that could stop new deaths were estimated as 78.8% for the European dataset and 90.7% for the complete one (see [3], thin black lines in figure 1). In five months, no critical values are visible, i.e., new deaths will appear even at 100% level of fully vaccinated people (see bold black lines in figure 1). This result can be explained by removal of restrictions for vaccinated persons.

The critical percentage of boosters x0 can be calculated by putting y = 0 into eq. (1):

$x_0=-\frac{a}{b}\text{ (5)}$

Using the values a = 8.4891 and b = -0.1080 from table 2, one can conclude that DDC values in Europe could tend to zero when the percentage of boosters exceeds 78.6% (see black solid line in figure 2). For the complete data set (the black dashed line in figure 2) no significant correlation between the DDC and BC values has been revealed since F/F_c(k₁,k₂)<1 (Table 2).

Fortunately, the mortality rate DDC/DCC always decreases with the increase of vaccination levels VC and BC (see table 2 and red lines in figures 1,2). The critical VC values (calculated with the use of eq. (5) and corresponding values a, b listed in table 2) are 82.5% and 81.0% for the European and complete datasets, respectively. Very close critical VC values yielded the statistical analysis of the data corresponding September 01, 2021, [3] (compare bold and thin red lines in figure 1). The critical BC values are 59.4% and 56.6% for the European and complete datasets, respectively (see red lines in figure 2). As of September 01, 2021 the DDC/DCC values were approximately 40% and 27% (for European and complete datasets, respectively) higher than the corresponding Omicron figures (compare thin and bold red lines in figure 1). This reduction of mortality rate may be associated with both the weakening of the pathogen and an increase in the number of people who have received natural immunity.

Table 2 illustrates that almost no statistically significant correlations were revealed for the daily tests per case ratio DTC. The only exception is the global relationship of DCC versus DTC, since F/F_c(k₁,k₂)>1 (see table 2, the dashed blue line in figure 3). Similar correlation was revealed in [3] for the ratio of accumulated numbers.

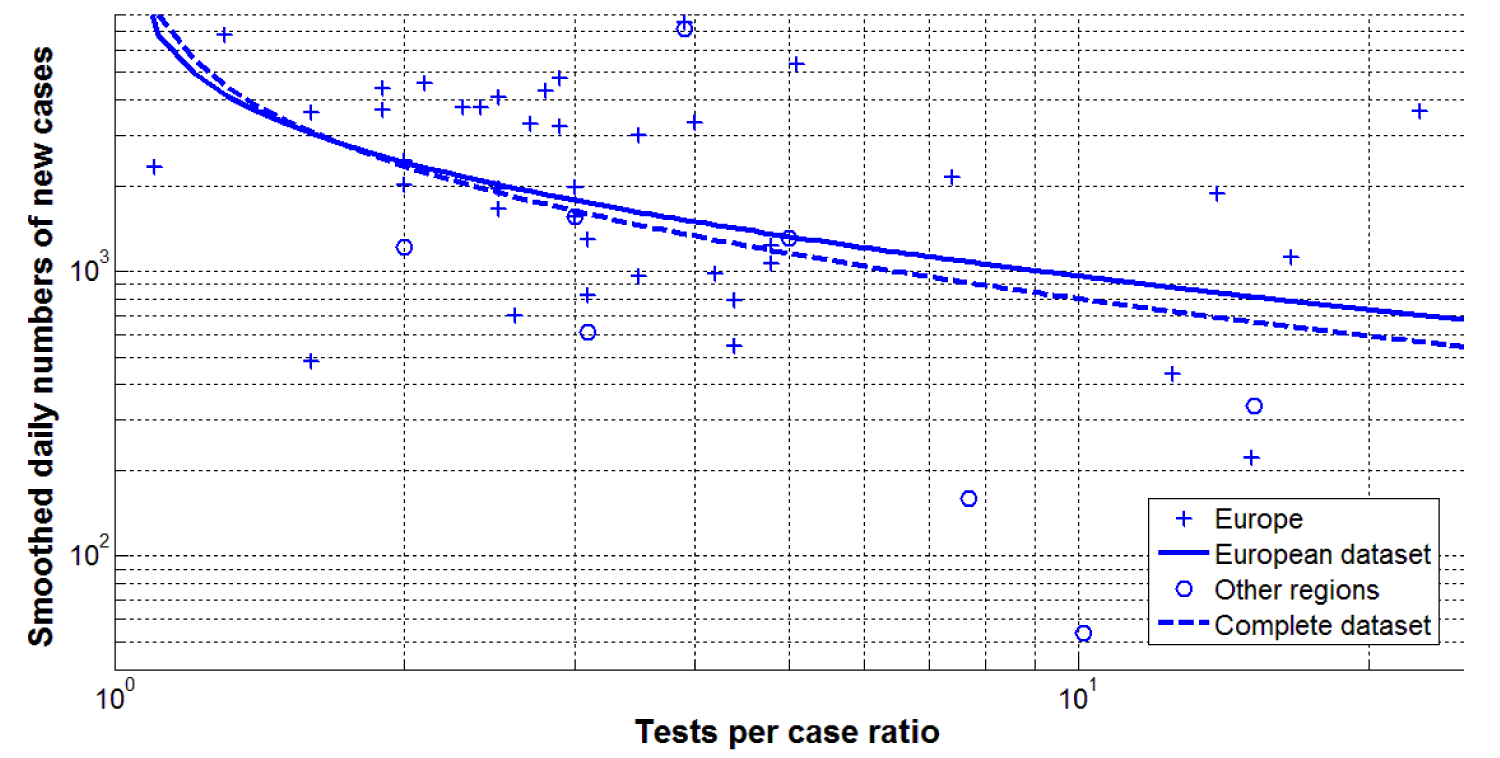
The absence of correlation for the European dataset forced applying the non-linear correlation (2) between DCC and DTC values. The optimal values of the additional parameters a and c were calculated (a = 219 and a = 214 for the European and global data sets, respectively; c = -1 in both cases). Rather high levels of the F/F_c(k₁,k₂) ratio (2.24 and 4.12 for the European and global data sets, respectively) show that the hypothesis (2) (or (3)) is supported by the results of observations (Table 1) at the confidence level 0.1. The best fitting lines can be written as follows:

$DCC=219+\frac{2196}{{(DTC-1)}^{0.4944}}\text{ (6)}$

$DCC=214+\frac{2126.7}{{(DTC-1)}^{0.5874}}\text{ (7)}$

for the European and complete datasets, respectively.

The relationships (6) and (7) are shown in figure 4 by the solid and dashed lines, respectively. It can be seen that the daily number of cases rapidly decreases as the increase of the tests per case ratio. Thus the increase of the tests per case ratio can be recommended as an effective tool to stop the COVID-19 pandemic. For example, very high testing levels allowed one to control the epidemic completely, (e.g., Hong Kong, Australia in 2020, see [1,3]).

Figure 4: Non-linear correlations between smoothed daily numbers of new cases and tests per case ratio as of February 01, 2022.
Best fitting lines (2) are solid for European datasets and dashed for complete datasets. “Crosses” represent the European datasets, “circles”-figures for other countries and regions available in table 1.

The values ​​of DDC and DDC/DCC do not show any visible correlation with the testing rate DTC (see table 2, black and red lines in figure 3). Since the numbers of deaths reflect the ability of patients to resist the captured strain and the level of medical care, DDC and DDC/DCC may be independent from the number of tests performed to identify one infected patient.

The presented statistical analysis has supported once more the fact that the vaccination itself cannot stop the COVID-19 pandemic. Vaccinated individuals can become re-infected and are just as dangerous to others as those who have not been vaccinated, [3,8]. Lifting of quarantine restrictions for vaccinated people has increased the number of infections (especially in highly vaccinated countries). The estimated number of persons spreading the infection in the whole world in mid-February 2022 can be around 8 million [16]. This huge value and rather small reduction of the mortality rate DDC/DCC makes it necessary to restore quarantine restrictions for both vaccinated and non-vaccinated persons.

Linear statistical analysis of the pandemic waves caused by SARS-CoV-2 omicron (B.1.1.529) in European and some other countries and regions (datasets corresponding to February 01, 2022) revealed that the numbers of new daily cases per capita DCC increase with the increase of the percentage of fully vaccinated people and boosters. For the percentage of fully vaccinated people this correlation was supported even at the confidence level 0.01. This result can be explained by removal of restrictions for vaccinated persons.

The mortality rates DDC/DCC demonstrate opposite trend and much higher confidence levels (e.g., 0.001). Thus, high levels of vaccinations and boosters significantly reduce the likelihood of a death for an infected person. Linear and non-linear regressions were used to find links between the DCC values and the tests per case ratio DTC. The non-linear dependences (6) and (7) were obtained at rather high confidence level. They show the significant decrease of the daily numbers of cases as the DTC values increase. Summing up, it can be argued that the COVID-19 pandemic can be controlled by restoring quarantine restrictions for both vaccinated and non-vaccinated persons and by increasing the tests per case ratio.

1. COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU).  https://bit.ly/38c3fSe
2. Nesteruk I, Rodionov O, Nikitin A.V, and Walczak S. Influences of seasonal and demographic factors on the COVID-19 pandemic dynamics. EAI Endorsed Transactions on Bioengineering and Bioinformatics. 2021;22(4):e2. doi: 10.4108/eai.8-12-2021.172364.
3. Nesteruk I, Rodionov O. Impact of vaccination and testing levels on the dynamics of the COVID-19 pandemic and its cessation. J Biomed Res Environ Sci. 2021 Nov 23;2(11):1141-1147. doi: 10.37871/jbres1361.
4. Fritz J, Herrick T, Gilbert SS. Estimation of health impact from digitalizing last-mile Logistics Management Information Systems (LMIS) in Ethiopia, Tanzania, and Mozambique: A Lives Saved Tool (LiST) model analysis. PLoS One. 2021 Oct 25;16(10):e0258354. doi: 10.1371/journal.pone.0258354. PMID: 34695158; PMCID: PMC8544866.
5. Nadimuthu LPR, Victor K. Environmental friendly micro cold storage for last-mile Covid-19 vaccine logistics. Environ Sci Pollut Res Int. 2022 Apr;29(16):23767-23778. doi: 10.1007/s11356-021-17584-2. Epub 2021 Nov 23. PMID: 34816344; PMCID: PMC8610367.
6. Adebimpe WO, Adeoye OA. Knowledge and practice of vaccination logistics management among primary health care workers in Nigeria. Hum Vaccin Immunother. 2021 May 4;17(5):1490-1495. doi: 10.1080/21645515.2020.1827609. Epub 2020 Nov 11. PMID: 33175641; PMCID: PMC8078657.
7. Sato R, Thompson A, Sani I, Metiboba L, Giwa A, Femi-Ojo O, Odezugo V. Effect of Vaccine Direct Delivery (VDD) on vaccine stockouts and number of vaccinations: Case study from Bauchi State, Nigeria. Vaccine. 2021 Mar 1;39(9):1445-1451. doi: 10.1016/j.vaccine.2021.01.037. Epub 2021 Feb 1. PMID: 33541796.
8. Nesteruk I. Influence of possible natural and artificial collective immunity on new COVID-19 pandemic waves in Ukraine and Israel. Explor Res Hypothesis Med. 2021;7(1):8-18. doi: 10.14218/ERHM.2021.00044.
9. Nesteruk I. COVID-19 pandemic dynamics. Springer Nature; 2021. doi: 10.1007/978-981-33-6416-5.
10. Nesteruk I. Visible and real sizes of new COVID-19 pandemic waves in Ukraine. Innov Biosyst Bioeng. 2021;5(2):85-96. doi: 10.20535/ibb.2021.5.2.230487.
11. Nesteruk I. Detections and SIR simulations of the COVID-19 pandemic waves in Ukraine. Comput Math Biophys. 2021;9:46-65. doi: 10.1515/cmb-2020-0117.
12. Alemu T, Jemal A, Gashe F, Suleman S, Sudhakar S, Fekadu G. Integrated pharmaceutical logistics system implementation in selected health facilities of Ethiopia: The case of four WOLLEGA ZONES. Res Social Adm Pharm. 2021 May;17(5):956-968. doi: 10.1016/j.sapharm.2020.07.026. Epub 2020 Aug 6. PMID: 32847732.
13. Draper NR, Smith H. Applied regression analysis. 3rd ed. John Wiley; 1998.
14. Appendix C. Statistical Tables. https://bit.ly/3LCLwko
15. Nesteruk I. Comparison of the fi rst waves of the COVID-19 pandemic in different countries and regions. In book: COVID19 pandemic dynamics. Springer Nature; 2021. doi: 10.1007/978-981-33-6416-5_7.
16. Nesteruk I. Epidemic waves caused by SARS-CoV-2 omicron (B.1.1.529) and pessimistic forecasts of the COVID-19 pandemic duration. MedComm (2020). 2022 Mar 9;3(1):e122. doi: 10.1002/mco2.122. PMID: 35281789; PMCID: PMC8906450.