Medicine Group . 2023 September 15;4(9):1290-1307. doi: 10.37871/jbres1798.
Complexity, Diversity, Homogeneity and Topology Measures Re-Define Biological Tumor Aggressiveness as a Function of Intercellular Connectivity
Przemyslaw Waliszewski*
- Fractal dimension
- Entropy
- Persistence homology
- Persistence homology entropy
- Persistence barcode entropy
- Bottleneck distance
- Wasserstein distance
- Growth
- Tumor aggressiveness
- Grading
- Prostate cancer
Abstract
Similarity between patterns of cellular self-organization in primary tumor and in its normal counterpart underlies the concept of biological tumor aggressiveness. That subjective parameter is supposed to correlate with both dynamics of local tumor growth and the risk of progression. Subjective evaluation during the microscopic examination is inaccurate. The co-application of fractal geometry and algebraic topology offers a novel perspective. A set of prostate carcinomas comprising all patterns of self-organization was classified according to complexity and entropy to investigate how complexity relates to topology of the patterns. Prostate carcinomas evolve from order to disorder along the increasing entropy as many physical dynamic complex systems do. Carcinomas can be classified into the classes of complexity equivalence according to both the values of the global fractal dimensions D0 or D1 and the Shannon entropy H. Topological measures, such as the bottleneck distance or the Wasserstein distance reveal different topology in very low- and low-aggressive prostate carcinomas (class C1, C2, C3) in comparison with high-aggressive carcinomas (class C6, C7). This is contingent on the appearance of infiltrating cancer cells. While the persistent homology entropy Hph remains similar in all classes, the persistent barcode entropy Hpb is significantly decreased in class C1 and increased in class C7 in comparison with the other ones. Patterns of self-organization can now be defined according to changes in intercellular connectivity by the set of complexity, diversity, homogeneity, and topology measures.
Introduction
Biological tumor aggressiveness is a fundamental concept in tumor pathology [1]. It is based on the idea of similarity between tumor tissue and normal one. According to that concept, tumor aggressiveness, that is, both local tumor growth and global progression in the form of metastases is lower if patterns of growth formed by cancer cells are like those formed by their normal counterparts. Pathologists make here an important tacit assumption. Morphological tumor structure visible in the histological image is a static spatial category. It is related statistically to tumor growth that is a dynamic temporal category. While the idea of time-space plays a minor role in biology compared to physics, identification of some statistical associations between those two categories during tumorigenesis is not only a great achievement of classical tumor pathology. First, those associations suggest that cancer is an interacting dynamic complex tissue system that influences its own time-space in an active manner. Second, changes in both the spatial distribution of information and interactions between cells must end up in different complexity, geometry, and topology of the emerging patterns of self-organization.
Evaluation of similarity between normal tissue and irregular, weird geometric patterns formed by cancer cells is both subjective and intuitive (reviewed and summarized in [1,2]). Nonetheless, the criteria for biological tumor aggressiveness underwent a validation process. In the case of prostate carcinomas, it was done against 20,000 prostatectomy specimens and at least 16,000 biopsy samples. Despite that large data base, the interobserver variability remains with 80% significantly large (reviewed in [3,4]). In addition, those criteria undergo continually further changes [5-7]. Recently, supervised machine learning algorithms, such as the instructed convolutional neural networks, became the subject of breathless headlines. They were applied to check if the automated classification of patterns of self-organization seen in prostate carcinomas could end up in a more accurate classification than that obtained by a panel of experts. According to those studies, convolutional neural networks do not achieve worse results than experts [8,9]. They also are not significantly better [10]. Some weaknesses in those studies are worth emphasizing. First, no set of reference images was applied in those studies that would be selected using some objective, quantitative criteria. Instead of that, the objective category, such as the set of images classified by a neural network was compared with the subjective category, that is a set classified by pathologists and treated arbitrarily as a frame of reference. This is both a forbidden logical operation in the category theory [11] and the example of a medical fallacy of the bandwagon type [12,13]. Second, there are the internal limits in the construction of convolutional neural networks leading to the lower accuracy of classification [14]. Third, the additional limit has a source in the Gödel incompleteness theorems [15,16]. In consequence, there is no way to verify if the classification generated by the network is true or not [17,18].
There is a need for quantitative parameters characterizing patterns of self-organization. In contrast to regular geometric shapes known from the Euclidean geometry, geometry of patterns of self-organization in prostate carcinomas cannot be described by lengths or angles. The application of some non-trivial approaches, such as fractal geometry, is necessary to describe differences between those patterns. The geometric model of prostate carcinoma enabled prediction of the mean values of the global fractal dimensions D0 and D1 for the spatial distribution of cancer cell nuclei [3]. Computer algorithms based on fractal geometry revealed that the spatial distribution of cancer cells had multifractal structure defined by a family of global fractal dimensions. The quantitative criteria for stratification of prostate carcinomas into the classes of complexity were proposed [4]. Using those criteria, one can construct the objective reference set for neural networking.
The relationship between the global information fractal dimension D1 and the Shannon entropy H [19,20] was also found in that study [4]. The values of two global fractal dimensions, D0 and D1, increased monotonically along the values of the Shannon entropy H. The patterns of self-organization increased their complexity while the spatial distribution of cancer cell nuclei changed from the structures of the higher order, such as glands to the structure of the lower order, such as cellular infiltrates. The existence of that relationship justifies the co-application of fractal geometry and algebraic topology for evaluation of weird shapes of those patterns. Fractal geometry deals with some properties of objects, such as size and relative position in relationship to the scale. Other than in the random networks governed by the Poisson distribution, fractal geometry characterizes the spatial distribution of cells by a family of both global and local fractal dimensions owing to the underlying power laws. Those laws imply that some structures of the higher order may possess greater significance for stability of cellular system. Topology investigates changes that occur in the geometric structure under continuous spatial transformations, such as stretching or bending. Those transformations are also associated with changes of the Shannon entropy.
The current study provides the answer to the question, whether transformation of the spatial distribution of cancer cell nuclei into the spatial intensity curve preserves the existing multifractal structure and how analysis of those curves enables prediction of the pattern stability. Patterns that cancer cells compose in space can be quantified by a set of complexity and topology measures. Those patterns can be classified into both seven classes of complexity equivalence and three classes of topological equivalence. Furthermore, each pattern can be transformed to the corresponding persistence homology diagram. Similarity between patterns of self-organization can be measured quantitatively by topological distance measures. Differences in self-organization of cancer cells result from alterations in intercellular connectivity.
Methods
Processing of images
This study was performed according to the ethical standards outlined in the WMA declaration of Helsinki “Ethical Principles for Medical Research Involving Human Subjects” (http://www.wma.net) as described previously in [3,4]. Since this project was based solely on computer-aided image analysis of the digitalized anonymous tissue slides of prostate carcinomas, no written consent from the prostate cancer patients was necessary. Tissue origin, processing of histological slides, digitalization and electronic isolation of cell nuclei were described previously [3,4]. The numbers of images representing all patterns of self-organization seen in prostate carcinomas, benign prostatic hyperplasia (BPH) and normal-appearing prostate epithelium (NAPE) used in this study are provided in in Tables 1,2.
| Table 1: Summary of the complexity measures, topological measures, and entropy. For the spatial distribution of cell nuclei values are provided as triplets, (i.e., mean, median and standard deviation reading from the top to the bottom of the column). REF stands for the Frame of Reference. BPH denotes benign prostatic hyperplasia, NAPE denotes normal-appearing prostate epithelium. The values of the global fractal dimensions and the Shannon entropy H increase monotonically, what defines classes of complexity equivalence. The differences for the D0, D1, H and Hpb are significant at p < 0.001. | |||||||||
| Measure | NAPE n = 10 |
BPH n = 40 |
C1 n = 21 |
C2 n = 21 |
C3 n = 26 |
C4 n = 20 |
C5 n = 20 |
C6 n = 20 |
C7 n = 20 |
| D0 | 1.315 1.336 0.012 |
1.490 1.503 0.099 |
1.471 1.460 0.044 |
1.559 1.561 0.019 |
1.595 1.590 0.013 |
1.640 1.640 0.007 |
1.669 1.667 0.011 |
1.737 1.737 0.018 |
1.795 1.793 0.024 |
| D1 | 1.319 1.341 0.014 |
1.519 1.523 0.102 |
1.505 1.509 0.020 |
1.557 1.556 0.024 |
1.594 1.592 0.016 |
1.641 1.638 0.011 |
1.674 1.662 0.031 |
1.728 1.730 0.021 |
1.759 1.753 0.015 |
| Shannon Entropy H |
0.386 0.393 0.010 |
0.594 0.601 0.030 |
0.610 0.618 0.042 |
0.687 0.683 0.019 |
0.744 0.741 0.016 |
0.804 0.798 0.015 |
0.848 0.844 0.013 |
0.931 0.932 0.010 |
0.978 0.979 0.015 |
| Persistence Homology Entropy Hph | 0.205 0.209 0.006 |
0.209 0.211 0.017 |
0.218 0.215 0.015 |
0.220 0.222 0.013 |
0.208 0.203 0.018 |
0.196 0.197 0.014 |
0.196 0.194 0.011 |
0.204 0.200 0.003 |
0.181 0.159 0.013 |
| Persistence Barcode Entropy Hpb |
0.354 0.365 0.012 |
0.438 0.438 0.073 |
0.373 0.360 0.058 |
0.509 0.489 0.034 |
0.574 0.577 0.051 |
0.578 0.580 0.045 |
0.547 0.547 0.033 |
0.614 0.614 0.017 |
0.720 0.712 0.054 |
| Bottleneck distance W∞ | REF | 24.385 20.101 10.245 |
20.629 21.606 3.875 |
16.749 15.624 4.077 |
15.444 15.293 3.075 |
21.807 22.120 3.759 |
24,435 23.638 2.944 |
26.318 25.634 2.277 |
28.295 29.222 1.405 |
| Wasserstein distance Wp = 1 | REF | 316.268 316.089 39.140 |
260.366 264.362 39.613 |
367.967 362.093 84.128 |
278.679 269.823 31.989 |
490.586 406.074 152.989 |
552.110 543.519 137.823 |
649.409 633.293 80.739 |
749.021 767.824 94.411 |
| Table 2: A summary of the values of both the fragmentation dimension and the embedding correlation dimension for the space series in all classes of equivalence C1-C7 as well as in benign prostatic hyperplasia. NAPE stands for normal-appearing prostatic epithelium, BPH denotes benign prostatic hyperplasia. The differences between classes of complexity equivalence for the fragmentation dimension are not statistically significant despite some tendency to monotonicity. The differences for the embedding correlation dimension are significant at p < 0.001. | |||||||||
| NAPE | BPH | Prostate Carcinomas | |||||||
| n = 10 | n = 40 | n = 21 | n = 21 | n = 26 | n = 20 | n = 20 | n = 20 | n = 20 | |
| Classes of Equivalence D0/D1 | |||||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | |||
| Fragmentation Dimension |
10.8925 10.5278 1.8216 |
14.8572 12.4600 8.3711 |
10.4444 9.9670 3.0758 |
9.9106 9.7595 2.8419 |
9.3559 9.2880 2.6509 |
8.1583 8.0390 3.3151 |
7.2600 7.0805 2.3292 |
6.7173 6.0150 2.4682 |
6.0499 5.9270 1.4062 |
| Fragmentation Coefficient | 27.2116 27.4692 2.5245 |
36.6200 31.5000 19.5635 |
25.0161 25.0000 6.6468 |
26.0000 24.5000 7.1386 |
23.3171 23.0000 6.1377 |
19.4706 20.0000 7.7469 |
17.0000 15.0000 5.5759 |
15.2759 15.0000 3.1836 |
17.5455 17.0000 5.4224 |
| Embeding Correlation Dimension |
2.1683 2.1052 0.2179 |
3.5316 3.2848 0.6234 |
2.3123 2.2419 0.2552 |
3.1216 3.1042 0.2178 |
4.5146 4.4497 0.2513 |
5.1435 5.2403 0.3023 |
5.6263 5.5386 0.2547 |
6.4546 6.4009 0.3058 |
7.4236 6.8345 0.4479 |
Synthesis of fractal dimensions, entropy and persistence homology
The spatial distribution of cell nuclei was characterized by several measures, such as the global capacity fractal dimension D0, the global information fractal dimension D1, Shannon entropy H, persistence barcode entropy Hpb, persistence homology entropy Hph, the bottleneck distance W∞, and the Wasserstein distance Wp. Figure 1 shows principles of both fractal and topological algorithms.
The global fractal dimensions of the Renyi family, i.e., capacity dimension D0 and information dimension D1 were measured in all images using software Benoit 1.3 (True Soft, USA, http://www.trusoft-international.com/benoit.html). The obtained values were verified against the predictions of the geometrical model described previously [3]. Multifractal spectra were obtained using the open-source software Image J ver 1.52 and open-source plugin FracLac 2013 Janb420 by A. Karperien (https://imagej.nih.gov/ij/plugins). The Shannon entropy H was measured for the spatial distribution of cancer cell nuclei in digitalized images using Matlab R2021b (MathWorks, USA, https://www.matlab.com).
Both persistence homology and persistence barcodes were generated for all images using two R packages, TDA and TDAStat (R ver. 4.2.0, https://www-r-project.org). Coordinates of cell nuclei in the two-dimensional space were obtained using Mathematica 13.0 (https://www.wolfram.com). Persistence barcode entropy Hpb was measured for the persistence barcodes using open-source Python package Persim ver. 0.3.1 (scikit-tda.org, https:// pypi.org/project/persim/). Persistence homology entropy Hph was measured for birth-death points in the persistence homology diagram using Matlab R2021b.
The statistical analysis was performed by Statistica version 8.0 (StatSoft, Tulsa, USA) and Sigma Plot ver. 14.0 (Systat Software Inc., San Jose, USA, https://www.sigmaplot.com). For each measure, the values of mean, median and standard deviation were obtained.
Multifractal spectra
The distribution of pixels in the image is determined by a box counting method. This distribution of pixels becomes the basis for a series of calculations described elsewhere by the equations 1-5 [21]. The probability, Pi, of several pixels, mi, appearing in the given box, i, is proportional to the box size, ε, and some exponent, αi. The exponent αi is constant for a monofractal but varies for the multifractal.
in which i is the index for each box laid over the set for ε, mi(ε) denotes the number of pixels or mass in any box i at size ε, Mε stands for the total mass or sum of the pixels in all boxes for that ε. A partition function, χq(ε), which varies with the moment order q and scale ε, was then calculated by equation 2:
A relationship between the partition function χq(ε) and scale ε has the algebraic form of the power law, and, therefore, the multifractal property exists, if the logarithm of the partition function χq(ε) changes linearly with the logarithm of scale with a slope of the mass exponent, τ(q) as in equation 3:
By plotting the curves of log χq(ε) against log(ε) at many moment orders q, one computes the generalized fractal dimension, D(q). The Hölder exponent, i.e., singularity index, α(q), with respect to variable mi, is computed according to equation 4:
And the single multifractal spectrum f(α(q)) will be calculated according to equation 5
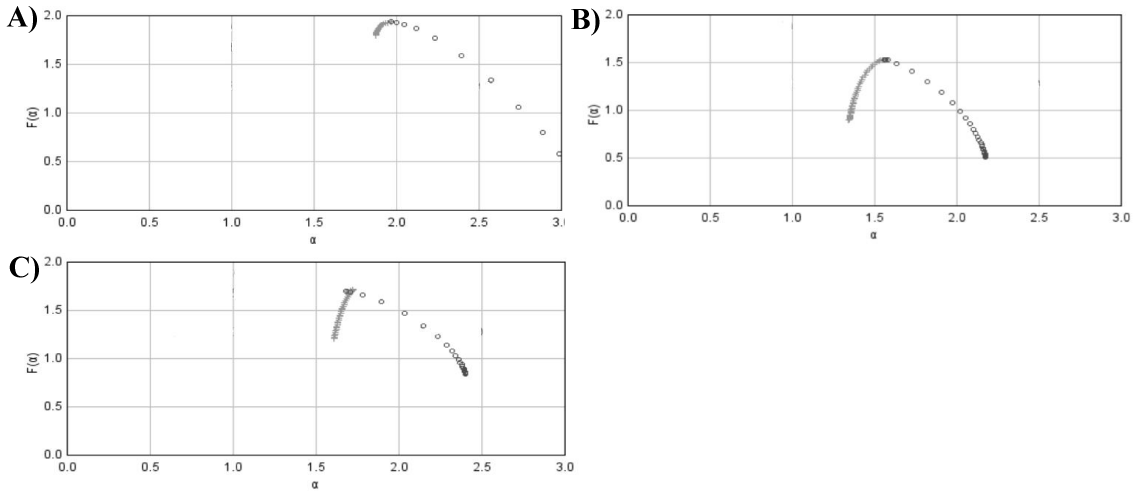
The singularity index α(q) is a measure of crowding of variable mi at the moment order q, when ε approaches zero. ƒ(α(q)) is also the fractal dimension of the subset of the variable mi with the specific singularity index α(q). The abundance of α(q), reflects the extent of spatial variability in the variable mi. The wider the multifractal spectrum, the greater α(q), and the greater is the spatial variability in distribution of the variable mi. In addition, with the amplification of high positive or negative q values, the spatial variability controlled by the higher or lower data values of variable mi is distinguished from each other and represented by the α(q), in the left and right parts of the multifractal spectrum, respectively. The α(q)max and α(q)min correspond to the singularity strength of the lowest and highest data values of the variable m, respectively. The single multifractal spectrum therefore can detect a spatial pattern and separate anomalous variation from the background variation.
Embedding correlation dimension
If a function C(ε) is the probability that two arbitrary points in a set are closer together than ε, the correlation dimension is given by the expression log(C)/log(ε) in the limit ε→0, and N→∞. A non-integer value of that expression defines the correlation fractal dimension. For the random series of numerical values, such as those representing the white noise, the correlation dimension graph is a straight line. Indeed, no matter how the white noise is embedded in the space, it fills that space evenly. Deterministic chaotic or periodic series have a distinct spatial structure, and the corresponding correlation dimension attains plateau at some point as the embedding dimension increases.
Non-stationarity
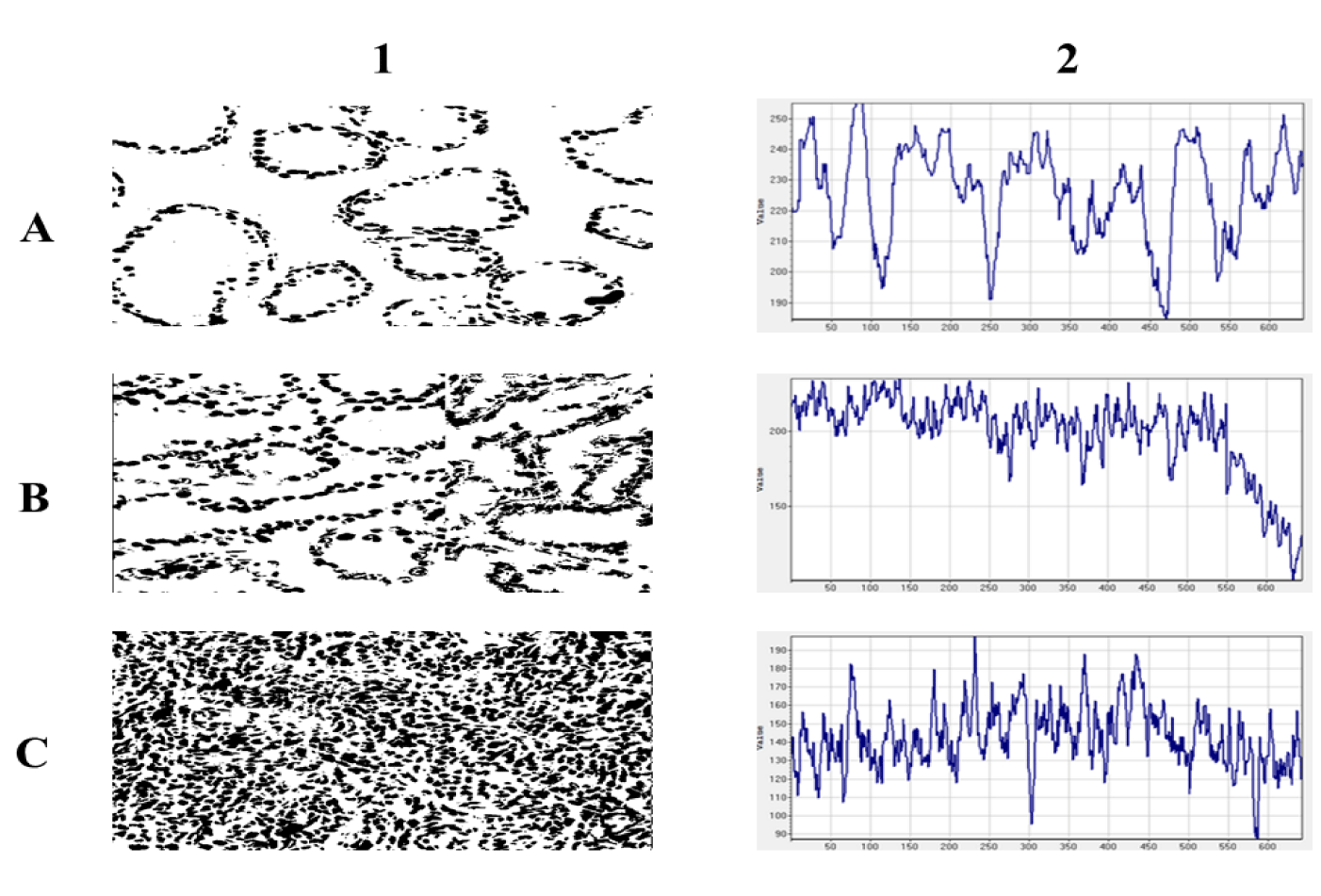
Normal glands are self-organized multicellular structures of higher order. The spatial distribution of cancer cell nuclei results from dynamic intercellular molecular interactions between epithelial cells and surrounding mesenchymal cells. Initially, cancer cells keep the ability to self-organize in similar gland structures as their normal counterparts do. Malignant epithelial cells infiltrate the entire available tissue space eventually. The geometric transformation of two dimensional, digitalized, black and white images of cancer cells nuclei present in tissue of prostate carcinomas was performed in such a manner that intensity of signal standing for cancer cell nuclei was measured along a chosen axis at the successive equally spaced points. The space series shown in figure 3 result from that transformation. Those spatial series represent a real stochastic process that is a mathematical object defined as a family of random variables in some probabilistic space. One of the realizations of that stochastic process is stationarity. Stationarity denotes that the statistical properties of the generating process do not change, that is, the mean, variance and autocorrelation function remain stable during the process. Such stationary series can be inverted. Forecasting as to the next values in the series can be made with a high accuracy because the way the process changes is linearly predictable. In other words, the test for stationarity answers a question if the spatial distribution of cancer cell nuclei is homogeneous, and if one can expect with a high probability that the spatial distribution of cell nuclei will remain stable within the other areas of the same carcinoma. The augmented Dickey-Fuller statistical test is usually sufficient for the evaluation of stationarity in time or spatial series. If the calculated test statistic is less (more negative) than the critical value, then the null hypothesis is rejected, no unit root is present in a spatial series, and the series is stationary. Otherwise, the series is non-stationary.
Fragmentation dimension and size-frequency algorithm
All grey intensity curves were analyzed by Size-Frequency algorithm (Benoit 1.3, Iskander Umarov, True Soft Int'l Inc., USA). Briefly, this algorithm takes a collection of objects of linear size x, and defines as n(x) the number of objects whose linear size is greater than x. If the set is distributed according to a power-law, it is a self-similar fractal, and the size-frequency (fragmentation) dimension is defined as the exponent d in the following equation 6:
Briefly, all the values taken by the variable x are sorted. For each value in the set xi one defines n(xi) as the number of elements whose x is greater than xi. If the set is fractal, a plot of the logarithm of n(xi) versus the logarithm of xi will be a straight line with a negative slope equal to d. In addition, each curve is a series. That series has two principal properties, its statistical distribution and its persistence. Their distribution can be evaluated using a plot of the raw size-frequency values and arithmetic axes.
Visual recurrence analysis and the recurrence plot
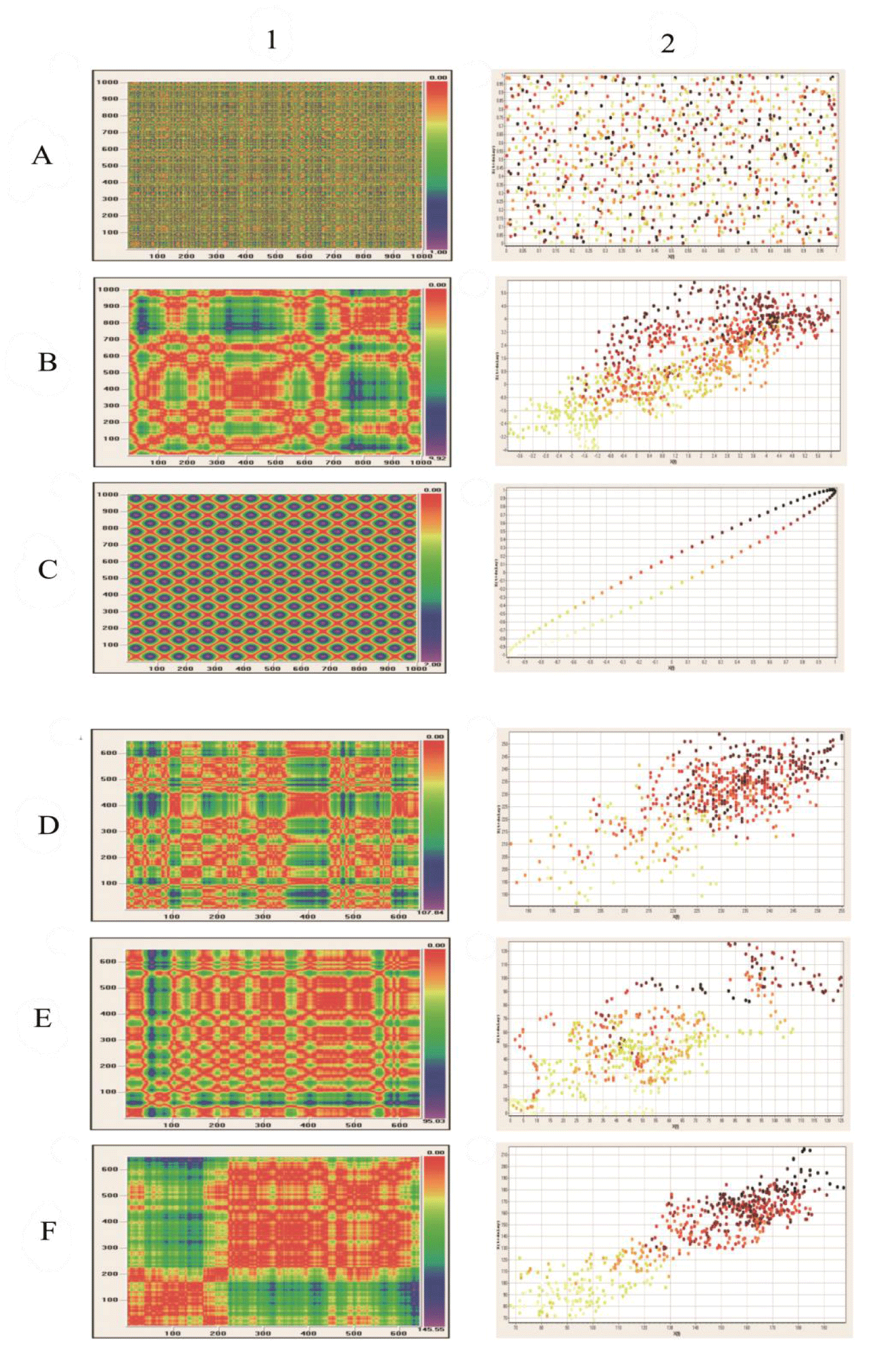
Visual recurrence analysis was performed using the VRA software version 4.9 written by Eugene Kononov in 2005 [22]. The VRA software detects hidden patterns across a one-dimensional series of scalar observations produced by a multidimensional system. If the underlying signal is truly random and has no structure, the distribution of colors over the recurrence plot is uniform and homogeneous. If there is some hidden order in the series of data, some characteristic distribution of colors can be seen in the recurrence plot reflecting the interactions of all variables that define this dynamic system [23].
Briefly, a one-dimensional series of numerical data is expanded into a multidimensional space, in which the underlying dynamic process occurs. Using a method of delayed coordinate embedding, a phase space portrait of the process will be deciphered from a single scalar series. First, one substitutes each observation in the original series X(t) with a vector yi = {xi, xi-d, xi-2d, … , xi-(m-1)d}, where i is the time or spatial index, m is the embedding dimension, d is the time delay or the spatial interval. In consequence, one gets a series of vectors: Y = {y1, y2, y3, …, yN-(m-1)d}, where N is the length of the original series. Each state St at step (or time t) is approximated by a vector of delayed coordinates Yt = { xt, xt-d, xt-2d, … , x1t - (m-1)d}. Once the system is reconstructed in a manner outlined above, a recurrence plot can be used to show which vectors in the reconstructed space are close and far from each other. More specifically, Visual Recurrence Analysis calculates the Euclidean distances between all pairs of vectors and codes them as colors. The recurrence plot is a color-coded matrix, where each [i][j]th entry is calculated as the distance between vectors Yi and Yj in the reconstructed series. After the distances between all vectors are calculated, they are mapped to colors from the pre-defined color map and are displayed as colored pixels in their corresponding places. A recurrence plot is a graphical representation of a correlation integral.
The bottleneck distance and the Wasserstein distance
The introduction to topology can be found elsewhere [24-26]. Those sources provide the most important definitions, such as open set [24], compactness as a property of a subset of Euclidean space being closed [24], connectedness of a topological space [25], and a homeomorphism as a continuous bijective mapping (function) between topological spaces [26].
Persistent homology is a method for computing topological features of a space at different spatial resolutions. More persistent features are detected over a wide range of spatial scales and are deemed more likely to represent true features of the underlying space rather than artifacts of sampling, noise, or a choice of parameters. Persistent homology identifies topological holes. [27].
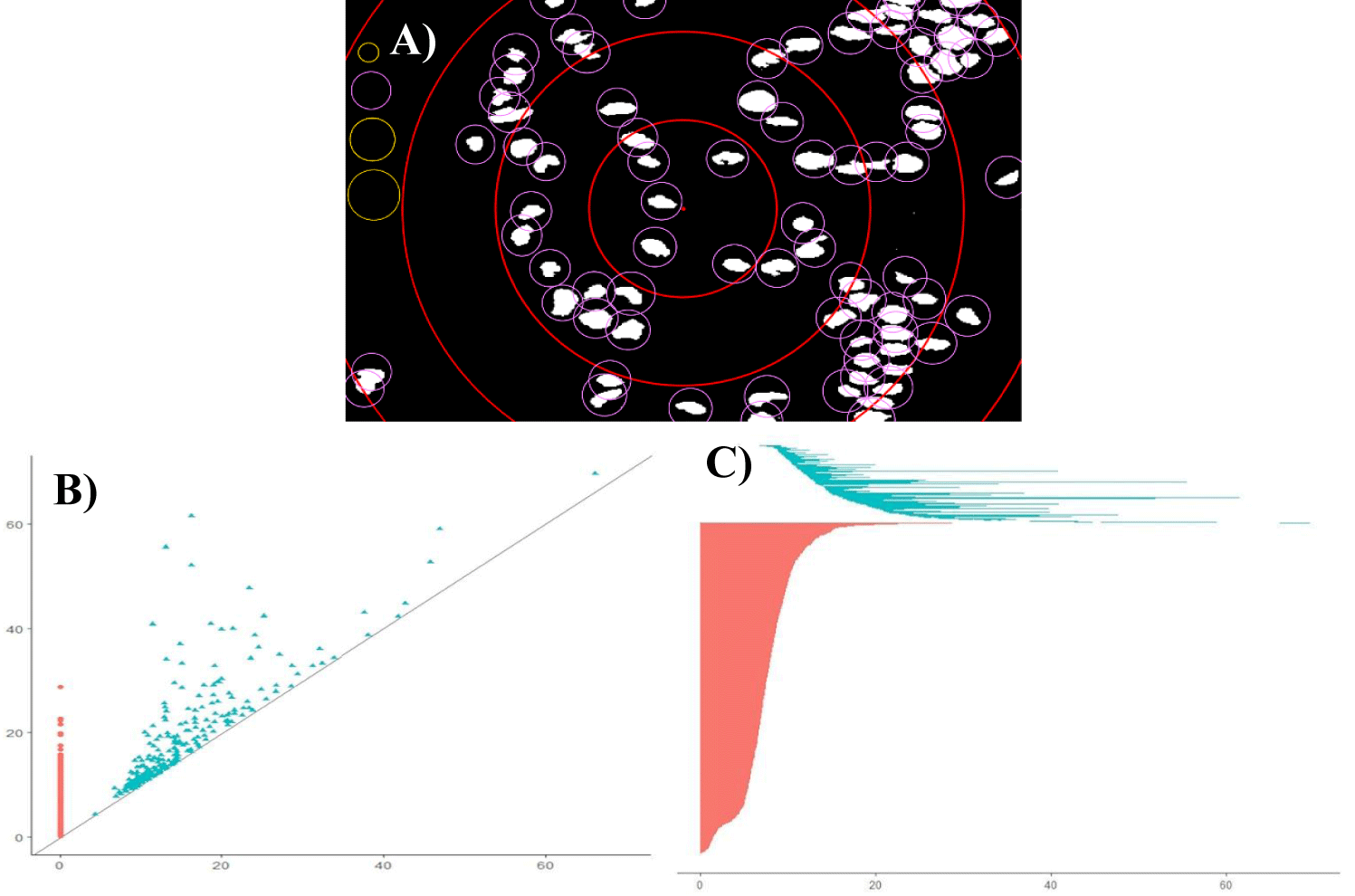
To find persistent homology of a given spatial structure, that structure must first be represented as a simplicial complex, that is, as a set of points, edges, triangles, and their n-dimensional counterparts. That simplicial complex undergoes a filtration process. The selected points will be covered by circles with increasing radiuses (Figure 1). If those coverings touch each other and form a loop, the birth of a topological hole, that is, a k-chain that is a combination of k-simplices, will be recorded on the persistence diagram. If the hole disappears eventually, that fact will be recorded on the diagram as a death of the hole. The number of emerging holes present within the topological structure will also be shown on the persistence diagram (see for details [28].
Topological analysis can be easily applied to characterize carcinomas, adenomas, or normal glands [29]. It is enough to obtain co-ordinates of cancer cell nuclei treating them as points in the two-dimensional surface. Then, both the number of loops (holes) as well as the number of individual points (cells) can be precisely calculated. The corresponding persistence diagrams rather than images of prostate tissue can be compared quantitatively to express differences between them [30,31]. That goal can be achieved by the application of two topological distance metrics, that is the bottleneck distance and the Wasserstein distance (Table 1).
The bottleneck distance measures the similarity between two persistence diagrams. It is the shortest distance for which there exists a perfect matching between the points of the two diagrams (completed with all the points on the diagonal to ignore cardinality mismatches). Any couple of matched points is at most at the given shortest distance, where the distance between points is the sup norm in R2 (not the Euclidean distance) [30].
The Wasserstein distance also measures the similarity between two persistence diagrams. The algorithm uses the sum of lengths of all edges instead of the shortest distance between the matched points.
Formally, the Wasserstein distance between two persistence diagrams X and Y defines equation 7:
where 1 and ϕ ranges over bijections between X and Y [32].
The bottleneck distance between two persistence diagrams X and Y is a special case of the Wasserstein distance, where p equals infinity and is given by equation 8:
Persistence entropy
The Shannon entropy H is a statistical measure of both the information content and diversity in each cell configuration in the image. It characterizes grey images or binary images of the spatial distribution of cancer cell nuclei [4]. The Shannon entropy H describes the following equation 9:
In the above equation, pj denotes the probability that the difference between two adjacent pixels of the image is equal to j. It is calculated from the histogram counts. Low entropy images, such as those containing mostly black background, e.g., in benign prostatic hyperplasia or in well-differentiated adenocarcinomas, have large numbers of pixels with the value zero. The black image that contains no white pixels will have entropy equal zero.
The entropy HD of a set with D dimensions is defined by the following equation 10:
ín which H stands for the Shannon entropy (see Equation 3), ε denotes size. In consequence, entropy H is a linear function of log ε with slope D and intersection HD. It is important to notice that the slope D in the limit for ε = 0 becomes the global information fractal dimension D1 [19].
Persistence entropy of barcodes Hpb is the Shannon entropy calculated for the persistence barcodes, using length of persistence intervals. It is defined by the known formula for the Shannon entropy (compare equation 11 with equation 9):
in which pi stands for the length of the barcode interval I divided by the sum of the lengths of all barcode intervals. The normalized persistence entropy obtains values between 0 and 1. It is calculated by dividing the above equation by the number of persistence intervals [33]. The application of those parameters enables subordination of carcinoma images according to the increasing amount of missing information.
Results
The entire spectrum of patterns of cellular self-organization seen in prostate carcinomas was studied in that project. The distribution of cancer cell nuclei in normal prostate epithelium, prostatic hyperplasia, and in adenocarcinomas has a structure of stochastic, finite multifractal (Table 1 and figure 2). That multifractal structure was found in all tissues analyzed. There was a linear relationship between the logarithm of a box size ε and the logarithm of the number of boxes N(ε) covering the entire set of cancer cell nuclei, what defines the global capacity fractal dimension D0 (Table 1). The linear relationship was also found between the logarithm of probability p of finding a pixel of the object under study in each box of size ε what defines the global information fractal dimension D1 (Table 1). The mean values are like those published previously [4]. The multifractal structure was identified even in carcinomas without the visible gland-like organization, with cell infiltrates dominating over the entire tumor structure. Using the key relationship between the Shannon entropy and the global information fractal dimension D1 given by equation 10, patterns of self-organization were subordinated to the classes of equivalence. As expected, both measures increased monotonically. The differences in the mean values between those classes were statistically significant (p < 0.001, t-Student test).
Figure 2 shows the course of the function f(α), that is, of the single multifractal spectrum for prostatic hyperplasia and for well-, intermediate- and poor-differentiated carcinomas. Those curves share some similarities. Interestingly, the curve for prostatic hyperplasia (Figure 2A) is almost identical with the curve corresponding to poor-differentiated carcinoma (Figure 2D). Although the histological images of those two entities look utterly different, the values of the Hölder exponent, α(q), that reflect the extent of spatial variability in the variable mi, are similar.
Figure 3 shows examples of the spatial transformation of the two-dimensional black and white images of cancer cell nuclei isolated from prostate carcinomas of the complexity class C1, C4 and C7 and their corresponding intensity non-ergodic curves. In general, prostate carcinomas possess distinct glands of varied sizes. Those structures are depicted in the space series characterized by both a low frequency and a high magnitude. If carcinoma has infiltrating cells exclusively, the corresponding space series has a high frequency and a low magnitude. There are also carcinomas that are in the critical stage of self-organization. They are composed of two co-existing organizations of gland-like structures and infiltrating cancer cells. That kind of co-existence appears for the first time in carcinomas of class C4. Since the emerging intensity curves evolve depending on the number of cell nuclei per spatial variable x, they can be analyzed as space series using methods developed for time series.
Transformation of the spatial distribution of pixels corresponding to cell nuclei in the histological images of prostate carcinomas, well-characterized previously by both the global capacity dimension D0 and the global information dimension D1, into the intensity curves preserves the existence of fractal structure. Figures 4 A1/A2-C1/C2 present results of the Visual Recurrence Analysis in the control package of spatially distributed points. The random distribution of points on a two-dimensional surface is represented by white noise. The distribution of points with fractal dimension is represented by the Henon attractor. The highly ordered distribution of points is represented by the sinus function. Figure 4 E1/2-F1/F2 show results of the Visual Recurrence Analysis in a set of prostate carcinomas belonging to the classes of complexity C1, C4, and C7. It should be noticed that infiltration of the entire surface in highly aggressive prostate carcinomas is not random. It also preserves Fractal structure is also preserved (Figure 4F(1,2)).
Both the fragmentation dimension and the embedding correlation dimension are fractal dimensions characterizing the space series (Figure 3). Their mean and median values in each class of complexity equivalence summarizes (Table 2). As expected, the mean values of the fragmentation dimension decrease monotonically from one class of complexity equivalence to the other. The curves given by equation 6 become steeper and steeper (plots not shown). However, the differences between the values of the fragmentation dimension for each class of complexity equivalence are not statistically significant. The embedding correlation dimension increases. In that case, the differences are statistically significant (p < 0.01). That latter finding proves the preservation of the fractal structure during the above-described transformation of the two-dimensional spatial distribution of cancer cell nuclei into the one-dimensional non-ergodic intensity curves.
Table 3 summarizes results of the augmented Dickey-Fuller statistical test for stationarity of those intensity curves. Non-stationarity abates a probability that the spatial organization within a given tumor remains identical in the other locations. The spatial series representing normal-appearing prostate epithelium and both carcinomas of the complexity class C1 and C2 are stationary. They possess the lowest values of standard deviation at p << 0.01. Non-stationarity emerges first in prostate carcinomas of the complexity class C4. Both the mean and the median value t are lower than the critical value t0 = - 3.43 at p = 0.01 for series with no stationary trend. Indeed, from one carcinoma of class C4 to the other one and from one area to the other one, the mix of glands and infiltrates looks in another way. It is impossible to predict the spatial distribution of cells in the other parts of tumor structure. Non-stationarity diminishes significantly in the next two classes C5 and C6, in which cell infiltrates dominate over gland-like structures. It vanishes completely in carcinomas of the class C7, in which are present cell infiltrates exclusively.
| Table 3: A summary of the results of the augmented Dickey-Fuller test for stationarity of the spatial series in all classes of equivalence C-C7 as well as in benign prostatic hyperplasia. The augmented Dickey-Fuller test evaluates the null hypothesis that there is a unit root in each series. The alternative hypothesis is that the series is stationary or trend stationary. The values of the augmented Dickey-Fuller t-distribution for the sample n = 643 points are as follows: t = - 3.43 at p = 0.01 for series with no trend and t = - 3.96 at p = 0.01 for series with a trend. NAPE stands for Normal-Appearing Prostatic Epithelium, BPH denotes Benign Prostatic Hyperplasia. | |||||||||
| Classes of Equivalence of Prostate Carcinomas | |||||||||
| t-value | NAPE | BPH | C1 | C2 | C3 | C4 | C5 | C6 | C7 |
| Mean | -5.7219 | -3.8324 | -4.2339 | -4.5519 | -4.7189 | -3.0429 | -4.2939 | -4.7883 | -5.3221 |
| Median | -5.7884 | -3.6977 | -4.3829 | -4.6105 | -4.4156 | -3.3878 | -4.3491 | -4.6668 | -5.4228 |
| SD | 0.3161 | 0.8257 | 0.4699 | 0.5787 | 0.4373 | 0.3953 | 0.7157 | 0.7623 | 0.6703 |
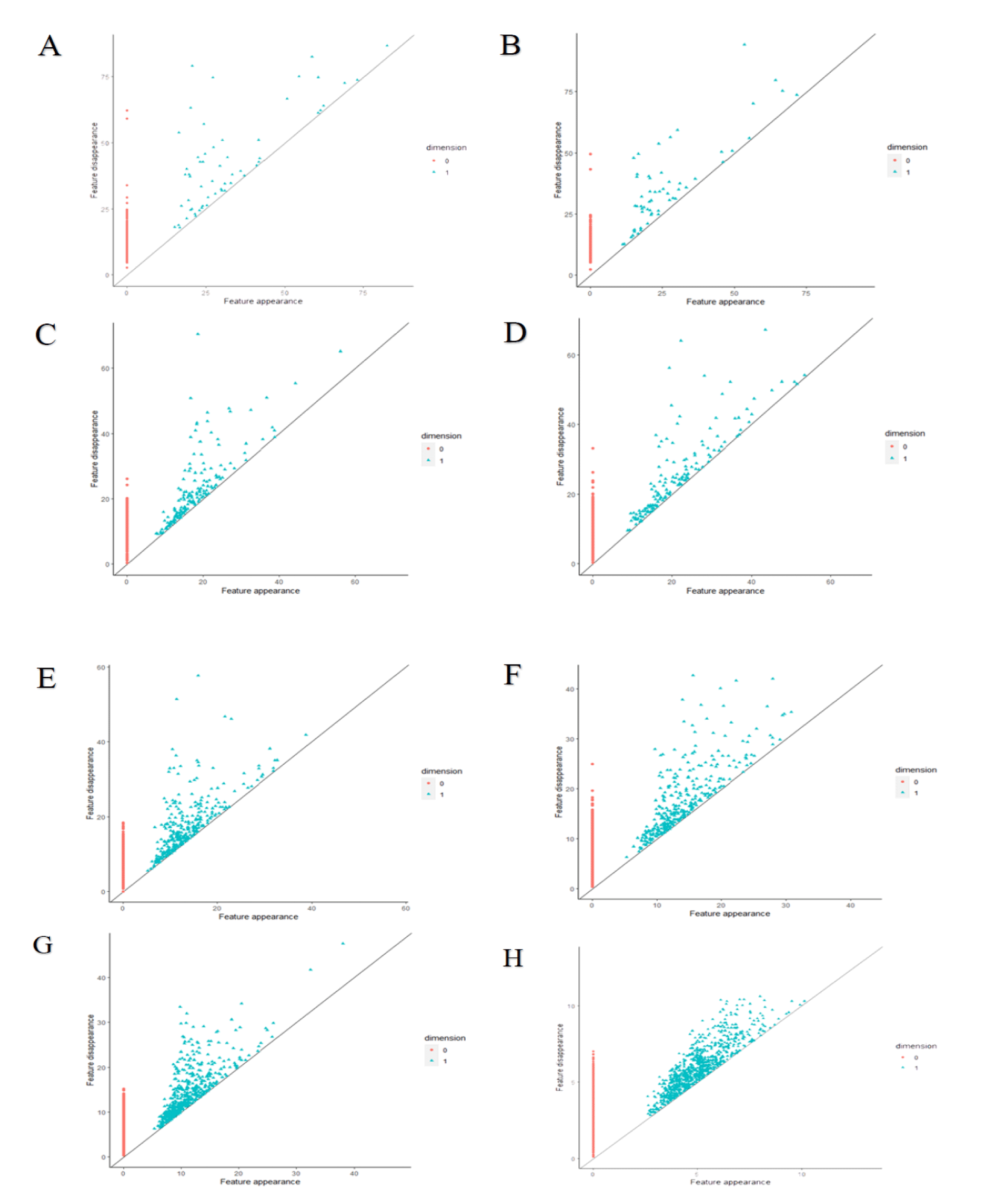
Persistence homology diagrams for the consecutive patterns of self-organization in prostate cancer shows figure 5. Points that stand for holes emerging in the topological structure of those carcinomas compose more and more compact set with decreasing scale (compare the feature appearance axes OX and the feature disappearance axes OY in each diagram). Various algorithms generate quite different results using the same images. Indeed, persistence homology entropy Hph does not increase at all (Table 1). Persistence barcode entropy Hpb does not pattern itself in each class of equivalence on the monotonicity of the Shannon entropy H that was calculated for the entire image. Hpb reaches the maximum for carcinomas of class C4. In that complexity class, infiltrating cancer cells appear for the first time and co-exist with gland-like structures. The latter ones are displaced gradually in the higher classes. The Hpb values increase again along the decreasing size of gland-like structures in carcinomas of class C6 to C7. As expected, those values for classes C6 and C7 remain larger than for classes C1, C2 and C3. The patterns in carcinomas of class C4 represent some novel, emerging topological entity with both different spatial organization and cellular interactions in comparison with the first three classes. The patterns of self-organization of carcinomas in class C7 seem to be random at first glance. However, persistent homology enables detection of some tiny loops composed of cancer cells.
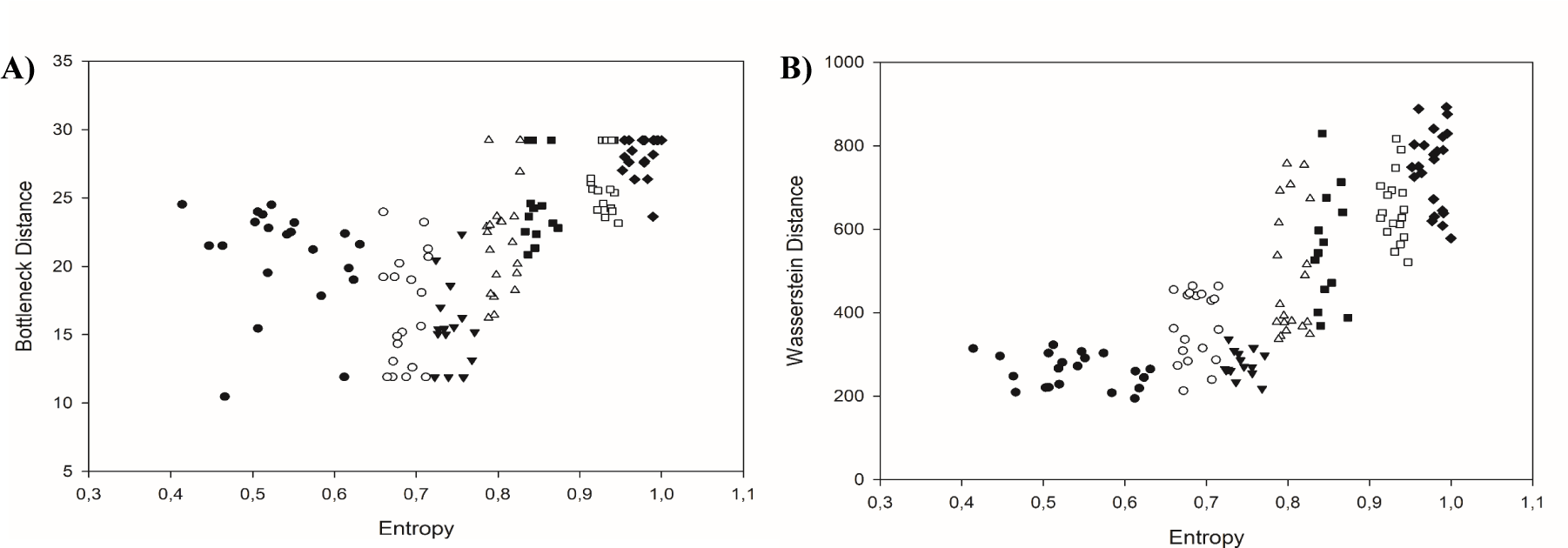
The bottleneck distance W∞ and the Wasserstein distance Wp were measured for prostate carcinomas in each class of equivalence using data generated by the corresponding persistence homology diagrams (Table 1 and figure 6(A,B)). Table 1 shows the mean, median and standard deviation values of both topological distances for classes of equivalence in prostate carcinomas and in adenomas compared to normal-appearing prostate epithelium. Both benign prostate adenomas and carcinomas of the complexity class C1-C3 possess similar values. Furthermore, those values classify the images of prostate carcinoma into three topological entities. The first topological entity includes carcinomas with low complexity as defined by the low values of both global fractal dimensions D0 and D1 as well as the low values of Shannon entropy H. They belong to the complexity class C1, C2 or C3 (Figure 6). Those carcinomas are in the early stages of tumorigenesis with well-preserved gland structure. The second topological entity includes carcinomas of the class C6 and C7. There are malignancies with infiltrating cells. Nonetheless, persistence homology reveals the existence of tiny loops composed of cancer cells that might be otherwise seen as random infiltrates. Those carcinomas are characterized by greater complexity. They have larger values of the Shannon entropy H as compared with the first topological entity. Those carcinomas present with increasing biological aggressiveness. Carcinomas of the class C4 or C5 compose the third set of malignancies with the intermediate topology (Figure 6). Carcinomas in that class are composed of a mix of gland-like structures and infiltrating cells. Some of those carcinomas have values of the Wasserstein distance typical of highly aggressive carcinomas of the class C6-C7. Some of the values overlap with those typical of the low aggressive carcinomas of the class C1-C3. It should be noticed that there is a significant difference between the values of both distances for carcinomas of the classes C1-C3 and C6-C7. Although that difference can be seen in the values of both distances, the Wasserstein distance reveals it in a more distinctive manner. High aggressive carcinomas are characterized by the Wasserstein distance above 500 and the bottleneck distance above 25 and the Shannon entropy above 0.9 (Figure 6).
Discussion
Prostate carcinomas are known as malignant tumors with tremendous morphologic variability. Self-organization of cells undergoing tumorigenesis is associated with the emergence of different temporo-spatial patterns of growth, such as glands, cords, rosettes, infiltrates, or their mix. Initially, cancer cells join and compose spatial patterns like normal ones do. More advanced carcinomas form a plethora of patterns with weird shapes. Some topological properties such as the Betti numbers corresponding to the numbers of cells, or the numbers of loops composed of those cells (holes) may vary between early and advanced carcinomas [34]. Those loops change both size and shape. Large, distinct loops decay in carcinomas with high complexity eventually. They will be replaced by smaller and smaller loops as well as by infiltrating cancer cells. The same evolution of patterns was observed in the current study, analyzed by persistence homology, and characterized by topological measures. Interestingly, those tiny loops do not disappear in most aggressive prostate carcinomas. The emergence of those loops may be independent of genetic alterations. Some experimental studies suggest that electrostatic potential generated by ion channels plays the regulatory role in cells undergoing self-organization into structures of the higher order [35-37].
Patterns of self-organization formed by prostate cancer cells occupy a certain time-space. The results show that the spatial distribution of cancer cells in prostate carcinomas has the structure of stochastic multifractals. The corresponding global fractal dimensions D0 and D1 increase their values in a monotonic way together with the increasing values of the Shannon entropy H. The same finding was seen in the previous study and applied to stratification of patterns of self-organization into classes of equivalence [4]. The existence of multifractal structure has been confirmed by two additional methods. First, transformation of the spatial distribution of cancer cell nuclei into the non-ergodic intensity curves, that is, the spatial series, enabled calculation of the values of the embedding correlation fractal dimension. In addition, preservation of the multifractal structure during that transformation was proven. Analysis of the corresponding spatial series enabled evaluation of stability of the spatial patterns of self-organization. As expected, that stability is the largest in the classes with stationary spatial series, that is, in classes with low or high aggressive carcinomas. Again, the spatial distribution of cancer cell nuclei in carcinomas of the class C4 generates non-stationary spatial series. That non-stationarity is caused by the co-existence of cell infiltrations and gland-like structures in various proportions. It disappears when infiltrations dominate over the entire image. Second, the Visual Recurrence Analysis generated both qualitative space diagrams and distance correlation diagrams. Using those diagrams, a random distribution of cancer cell nuclei or their highly regular distribution in tumor tissue can be excluded (Figure 4). Again, those diagrams indicate the existence of multifractal distribution.
The values of the single multifractal spectrum f(α) conform to the evolution of the local structure correlation diagram, the other measure of the spatial distribution of cell nuclei, seen in one of the previous studies [38] (Figure 2). This finding reflects a continuous evolution of patterns of self-organization and inversion caused by replacement of structures of the higher order with low complexity, such as glands by infiltrating cancer cells. Indeed, patterns of self-organization with low complexity emerge in the initial stages of tumorigenesis. They dominate over freely infiltrating cancer cells despite the increasing complexity of patterns during evolution as found by the increasing values of the Shannon entropy H. Finally, patterns of the higher order are replaced by infiltrating cancer cells. Those transformations cause changes in the amount of space occupied by cells. First, cancer cells are bound in loops. The areas free of cancer cells dominate. At the end of the pattern evolution, almost the entire available space is covered by infiltrating cancer cells. Indeed, entropy determines the evolution of complex systems. Evolution ends up when both entropy and complexity achieve maximal values (Table 1 and figure 6). The global fractal dimensions approach at that stage the values close to 2.000. Intercellular connectivity is the lowest, what facilitates infiltration of the surroundings or metastasis formation. It should be noticed that the increasing values of the global fractal dimensions D0 and D1 reflect changes in intercellular connectivity [39,40]. If elements of a dynamic system do not interact each other and fill the entire available space randomly, like molecules of neutral gas filling up a container evenly, then the dimension of the dynamic system equals the integer Euclidean dimension of the container. If connectivity of the interacting elements, i.e., interconnectedness which denotes the existence of complex, dynamic relationships in a population of cells leading to the spatial and temporal emergence of global features in the system that would never appear in a single cell existing out of the system [41], increases within the dynamic system, then the spatial fractal dimension characterizing complexity of that system is lower than the Euclidean dimension. The third possibility, that is, fractal dimension of the system is greater than the Euclidean dimension of the surrounding is a special case. It occurs if elements of a dynamic system continue to interact while the system is moved from the Euclidean space with the larger integer dimension to the space with the lower integer dimension (see for details [40,41]). The values of the global fractal dimensions D0 or D1 indicate whether intercellular connectivity is strong as in low aggressive carcinomas with low complexity, or weak as in highly aggressive carcinomas with increased complexity. Those intercellular interactions are quantified by the coefficient of cellular expansion. This is a function defined as a ratio between the integer dimension of the Euclidean space, in which growth, proliferation and self-organization of cells occurs and the global spatial capacity fractal dimension D0 of the complex system that characterizes the spatial distribution of epithelial cells. This function relates in the indirect way complexity of the system of interacting elements with their capacity for interactions. The Fibonacci constant defines the absolute limit for the above-mentioned ratio in the case of self-organization of cells into structures of the higher order, such as glands [40,42]. For cancer cell infiltrations, the value of that function approaches zero. In addition, intercellular interactions can also be further characterized by a family of the local fractal dimensions. Cancer cells with the local fractal dimension close to the integer value can easily metastasize since their intercellular connectivity is extremely low [40,42].
The intuitive concept of biological tumor aggressiveness is based on indeterminate similarity between normal and tumor tissue. Subjective examination of tumor tissue morphology enables a rough evaluation of underlying patterns of growth. Those patterns are usually inhomogeneous. Different patterns of self-organization, such as glands, cords, rosettes co-exist with infiltrating cancer cells randomly distributed in tumor tissue. Experimental findings of this study and the previous one [37] imply that the classical concept of biological tumor aggressiveness and tumor grading based on morphological similarities should be replaced by the quantitative evaluation of intercellular connectivity. In addition, persistence homology diagrams can be obtained for each carcinoma image. This approach can identify important topological features in data across multiple scales. Persistence homology diagrams can be compared with a frame of reference, such as the persistence homology diagram for normal-appearing prostate epithelium. This can be done by application of topological measures, such as the Wasserstein distance. Those diagrams can also be characterized with the additional quantitative measures, such as persistence homology entropy, persistence barcode entropy, and persistence homology fractal dimension [43].
Since a digitalized image is a snapshot of a mathematical function of two variables that determine spatial localization of cancer cells, the spatial distribution of cancer cells can be characterized by those measures objectively and unequivocally. The novel topological measures persistence homology entropy Hph, persistence barcode entropy Hpb, Wasserstein distance Wp, and bottleneck distance W∞ enable further characterization of patterns of self-organization and separate carcinomas with low complexity and low entropy (and low aggressiveness) from those with high complexity and high entropy (and high aggressiveness). However, one should keep in mind three facts. First, two objects with identical geometry may have different topologies and vice versa (Figure 6B). Second, closely related algorithms may produce different results (compare figure 6A,6B and Table 1 for the values of Hph and Hpb). Carcinomas of the class C1 to C3, that differ in values of entropy, fractal dimensions, and aggressiveness, have the Wasserstein or bottleneck distance in a similar range. In the class C4 or C5, some carcinomas have topological distances in the range typical of carcinomas of the first three classes, while the others have values typical of high aggressive carcinomas of the class C6 and C7. The well-known interobserver variability in grading or progression risk assessment by pathologists may have their common source in the geometric and topological overlapping. That phenomenon may also lead to an irremovable erroneous stratification by neural networks. Third, it was demonstrated by topological data analysis that breast carcinomas with similar tumor structure possessed both different patterns of gene expression and prognosis [44]. Hence, prostate carcinomas with patterns of self-organization in the same complexity or topology class characterized by the same values of parameters may also differ in profiles of gene expression, and, therefore, reveal different phenotypic features, growth potential, and prognosis.
Computer simulations [45,46] or experimental models [47-50] show a relationship between intercellular connectivity and emerging patterns of self-organization. That relationship can be described accurately by a combination of both geometric and topological measures [34], such as continuous quantitative measures of complexity, diversity, homogeneity, entropy, persistence entropy and topological distances. The latter ones enable a direct, objective comparison of tumor structure represented by cancer cells distributed in space with a normal-appearing tissue used as a frame of reference. The first evaluation of prostate carcinoma structure by persistent homology was performed in 2019 [29]. Authors applied algorithms of persistence homology to images classified according to the subjective Gleason grading system to search for differences between mixed spatial configurations of cancer cells associated with subjectively defined Gleason grades. They were still able to cluster prostate carcinomas into groups with dominant architectural patterns consistent with the continuum of Gleason patterns by using a ranked persistence vector. However, the number of prostate carcinomas was too low to make sure that this would be the case with any pattern of self-organization.
Using the above-mentioned criteria, one can select an objective reference set of tumor images for neural networking or self-organized mapping without a need of any reference to the subjective Gleason grading. Also, each new carcinoma can be compared with carcinomas already present in the database [51]. It should be noticed that the novel, objective approach must not be validated against the subjective Gleason scoring for the sake of permanency of principles of natural sciences [40,51].
In summary, the following findings must be reiterated. First, prostate cancer is a complex dynamic tissue system that evolves over time from order to disorder, towards the maximal entropy, as many complex physical systems do. Second, benign prostatic hyperplasia cannot be applied as a normal frame of reference. Third, the spatial distribution of cancer cells holds a power law as shown by both multifractal image analysis and spatial series analysis. Fourth, monotonically increasing values of the global fractal dimensions D0 and D1 (complexity measures) and the Shannon entropy H (both complexity and diversity measure) enable the objective stratification of patterns of self-organization into classes of equivalence. The (D0/D1, H)-stratification enables the proper choice of a reference set for neural networking. Fifth, topological measures show that the appearance of infiltrating cancer cells in carcinoma structure in the class C4 implies a shift in topology. Sixth, geometric and topological overlapping may influence accuracy of neural networking. Seventh, all measures indicate a leading role of intercellular connectivity as a force underlying self-organization of cellular patterns.
Declarations
Ethical Approval: Not applicable
Competing interests: None to declare
Authors' contributions: Not applicable
Funding: None
Availability of data and materials: Not applicable
References
- Kweldam CF, van Leenders GJ, van der Kwast T. Grading of prostate cancer: a work in progress. Histopathology. 2019 Jan;74(1):146-160. doi: 10.1111/his.13767. PMID: 30565302; PMCID: PMC7380027.
- Paner GP, Gandhi J, Choy B, Amin MB. Essential Updates in Grading, Morphotyping, Reporting, and Staging of Prostate Carcinoma for General Surgical Pathologists. Arch Pathol Lab Med. 2019 May;143(5):550-564. doi: 10.5858/arpa.2018-0334-RA. Epub 2019 Mar 13. PMID: 30865487.
- Waliszewski P, Wagenlehner F, Gattenlöhner S, Weidner W. On the relationship between tumor structure and complexity of the spatial distribution of cancer cell nuclei: a fractal geometrical model of prostate carcinoma. Prostate. 2015 Mar 1;75(4):399-414. doi: 10.1002/pros.22926. PMID: 25545623.
- Waliszewski P. The Quantitative Criteria Based on the Fractal Dimensions, Entropy, and Lacunarity for the Spatial Distribution of Cancer Cell Nuclei Enable Identification of Low or High Aggressive Prostate Carcinomas. Front Physiol. 2016 Feb 11;7:34. doi: 10.3389/fphys.2016.00034. PMID: 26903883; PMCID: PMC4749702.
- Montironi R, Cheng L, Lopez-Beltran A, Scarpelli M, Mazzucchelli R, Mikuz G, Kirkali Z, Montorsi F. Original Gleason system versus 2005 ISUP modified Gleason system: the importance of indicating which system is used in the patient's pathology and clinical reports. Eur Urol. 2010 Sep;58(3):369-73. doi: 10.1016/j.eururo.2010.04.028. Epub 2010 May 8. PMID: 20478652.
- Epstein JI, Egevad L, Amin MB, Delahunt B, Srigley JR, Humphrey PA; Grading Committee. The 2014 International Society of Urological Pathology (ISUP) Consensus Conference on Gleason Grading of Prostatic Carcinoma: Definition of Grading Patterns and Proposal for a New Grading System. Am J Surg Pathol. 2016 Feb;40(2):244-52. doi: 10.1097/PAS.0000000000000530. PMID: 26492179.
- Pudasaini S, Subedi N. Understanding the gleason grading system and its changes. J Path Nepal. 2019;9(2):1580-1585. doi 10.3126/jpn.v9i2.25723.
- Ström P, Kartasalo K, Olsson H, Solorzano L, Delahunt B, Berney DM, Bostwick DG, Evans AJ, Grignon DJ, Humphrey PA, Iczkowski KA, Kench JG, Kristiansen G, van der Kwast TH, Leite KRM, McKenney JK, Oxley J, Pan CC, Samaratunga H, Srigley JR, Takahashi H, Tsuzuki T, Varma M, Zhou M, Lindberg J, Lindskog C, Ruusuvuori P, Wählby C, Grönberg H, Rantalainen M, Egevad L, Eklund M. Artificial intelligence for diagnosis and grading of prostate cancer in biopsies: a population-based, diagnostic study. Lancet Oncol. 2020 Feb;21(2):222-232. doi: 10.1016/S1470-2045(19)30738-7. Epub 2020 Jan 8. Erratum in: Lancet Oncol. 2020 Feb;21(2):e70. PMID: 31926806.
- Nagpal K, Foote D, Tan F, Liu Y, Chen PC, Steiner DF, Manoj N, Olson N, Smith JL, Mohtashamian A, Peterson B, Amin MB, Evans AJ, Sweet JW, Cheung C, van der Kwast T, Sangoi AR, Zhou M, Allan R, Humphrey PA, Hipp JD, Gadepalli K, Corrado GS, Peng LH, Stumpe MC, Mermel CH. Development and Validation of a Deep Learning Algorithm for Gleason Grading of Prostate Cancer From Biopsy Specimens. JAMA Oncol. 2020 Sep 1;6(9):1372-1380. doi: 10.1001/jamaoncol.2020.2485. PMID: 32701148; PMCID: PMC7378872.
- Bulten W, Kartasalo K, Chen PC, Ström P, Pinckaers H, Nagpal K, Cai Y, Steiner DF, van Boven H, Vink R, Hulsbergen-van de Kaa C, van der Laak J, Amin MB, Evans AJ, van der Kwast T, Allan R, Humphrey PA, Grönberg H, Samaratunga H, Delahunt B, Tsuzuki T, Häkkinen T, Egevad L, Demkin M, Dane S, Tan F, Valkonen M, Corrado GS, Peng L, Mermel CH, Ruusuvuori P, Litjens G, Eklund M; PANDA challenge consortium. Artificial intelligence for diagnosis and Gleason grading of prostate cancer: the PANDA challenge. Nat Med. 2022 Jan;28(1):154-163. doi: 10.1038/s41591-021-01620-2. Epub 2022 Jan 13. PMID: 35027755; PMCID: PMC8799467.
- Spivak DI. Category theory for the sciences. Cambridge: The MIT Presss; 2014. p.203-314.
- Rikkers LF. The bandwagon effect. J Gastrointest Surg. 2002 Nov-Dec;6(6):787-94. doi: 10.1016/s1091-255x(02)00054-9. PMID: 12504215.
- Cohen L, Rothschild H. The bandwagons of medicine. Perspect Biol Med. 1979 Summer;22(4):531-8. doi: 10.1353/pbm.1979.0037. PMID: 226929.
- Li W, Li J, Sarma KV, Ho KC, Shen S, Knudsen BS, Gertych A, Arnold CW. Path R-CNN for Prostate Cancer Diagnosis and Gleason Grading of Histological Images. IEEE Trans Med Imaging. 2019 Apr;38(4):945-954. doi: 10.1109/TMI.2018.2875868. Epub 2018 Oct 12. PMID: 30334752; PMCID: PMC6497079.
- Gödel K. Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, I", Monatshefte für Mathematik und Physik, 1931;38(1):173–198. doi:10.1007/BF01700692.
- Gödel K. Some basic theorems on the foundations of mathematics and their implications. In: Feferman S, editor. Kurt Gödel Collected works. Vol. III, Oxford University Press; 1995. p.304-323.
- Heaven D. Why deep-learning AIs are so easy to fool. Nature. 2019 Oct;574(7777):163-166. doi: 10.1038/d41586-019-03013-5. PMID: 31597977.
- Colbrook MJ, Antun V, Hansen AC. The difficulty of computing stable and accurate neural networks: On the barriers of deep learning and Smale's 18th problem. Proc Natl Acad Sci U S A. 2022 Mar 22;119(12):e2107151119. doi: 10.1073/pnas.2107151119. Epub 2022 Mar 16. PMID: 35294283; PMCID: PMC8944871.
- Sethna JP. Statistical mechanics. Entropy, order parameters, and complexity. Oxford: Clarendon Press. 2011;101-102. doi:10.1093/oso/9780198865247.001.0001.
- Kristiansen G, Epstein JI. Immunohistochemistry in prostate pathology. IHC Prostate Pathology. DAKO. 2013.
- Salat H, Murcio R, Arcaute E. Multifractal methodology. Physica A. Statistical Mechanics and its applications. 2017; 473:467-487. doi.10.1016/j.physa.2017.01.041.
- Eckmann JP, Kamphorst SO, Ruelle D. Recurrence plots of dynamical systems. Europhys Letter. 1987;4(9):973-977. doi:10.1209/0295-5075/4/9/004.
- Takens F. Detecting strange attractors in turbulence. In: Rand D, Young LS, editors. Dynamical Systems and Turbulence. Lecture Notes in Mathematics. Berlin, Heidelberg:Springer. 1980. doi: 10.1007/BFb0091924.
- Morris SA. Topology without tears; 2020. p.25.
- Munkres J. Topology. Prentice Hall; 2000. p.148.
- Gamelin TW, Greene RE. Introduction to topology. Dover Publications; 1999. p.67
- Zomorodian A, Carlsson GE. Computing persistent homology. Discrete Computational Geometry. 2005;33(2):249-274. doi.10.1007/s00454-004-1146-y.
- Morozov D, Edelsbrunner H. A practical guide to persistent homology. Lawrence Berkeley National Lab. 2022.
- Lawson P, Sholl AB, Brown JQ, Fasy BT, Wenk C. Persistent Homology for the Quantitative Evaluation of Architectural Features in Prostate Cancer Histology. Sci Rep. 2019 Feb 4;9(1):1139. doi: 10.1038/s41598-018-36798-y. PMID: 30718811; PMCID: PMC6361896.
- Kerber M, Morozov D, Nigmetov A. Geometry helps to compare persistence diagrams. J Exp Algorithmics. 2017;22(1):1-20. doi:10.1145/3064175.
- Kerber M, Lesnick M, Oudot S. Exact computation of the matching distance on 2-parameter persistence modules. JoCG. 2020;11(2):4-25.
- Munch, E. Application of persistent homology to time varying systems. Duke University. 2013.
- Saul N, Tralie Ch. Scikit-TDA: Topological data analysis for python. Zenodo. 2019. doi: 10.5281/zenodo.2533369.
- Waliszewski P, Banaszak G. Topological evaluation of intercellular connectivity in adenocarcinomas. Proceedings of the 23rd International Conference on Control Systems and Computer Science (CSCS21). 2021. doi: 10.1109/CSCS52396.2021.00042.
- Levin M. Bioelectric signaling: Reprogrammable circuits underlying embryogenesis, regeneration, and cancer. Cell. 2021 Apr 15;184(8):1971-1989. doi: 10.1016/j.cell.2021.02.034. Epub 2021 Apr 6. PMID: 33826908.
- Carvalho J. A computational model of cell membrane bioelectric polarization and depolarization, connected with cell proliferation, in different tissue geometries. J Theor Biol. 2023 Jan 21;557:111338. doi: 10.1016/j.jtbi.2022.111338. Epub 2022 Nov 4. PMID: 36343668.
- Bates E. Ion channels in development and cancer. Annu Rev Cell Dev Biol. 2015;31:231-47. doi: 10.1146/annurev-cellbio-100814-125338. PMID: 26566112.
- Tanase M, Waliszewski P. On Complexity and homogenity measures in predicting biological aggressiveness of prostate cancer; implication of the cellular automata model of tumor growth. Journal of Surgical Oncology. 2015;112(8):791-801. doi: 10.1002/jso.24069.
- Waliszewski P. The circular fractal model of adenocarcinomas and tumor aggressiveness. Banach Center Publications. 2016;109:183-196. doi: 10.4064/bc109-0-12.
- Waliszewski P. The Fibonacci constant and limits of tissue self-organization; local complexity measures in evaluation of the risk of metastasis formation. Banach Center Publications. 2021;124:143-157. doi: 10.4064/bc124-12.
- Waliszewski P, Konarski J, Molski M. On the modification of fractal self-space during tumor progression. Fractals 2000;8(2):195-203. doi: 10.1142/S0218348X00000214.
- Waliszewski P. The Fibonacci constant, the Wasserstein distance, and biological tumor aggressiveness in prostate cancer. Proceedings of the 24th International Conference on Control Systems and Computer Science (CSCS23). 2023. doi: 10.1109/CSCS59211.2023.00043.
- Adams H, Aminian M, Farnell E, Kirby M, Peterson Ch, Mirth J, Neville R, Shipman P, Shonkwiler C. A fractal dimension for measures via persistent homology. In: Baas N, Carlsson G, Quick G, Szymik M, Thaule M, editors. Topological Data Analysis. Abel Symposia. 2020;15:1-31. Springer, Cham. doi: 10.1007/978-3-030-43408-3_1.
- Nicolau M, Levine AJ, Carlsson G. Topology based data analysis identifies a subgroup of breast cancers with a unique mutational profile and excellent survival. Proc Natl Acad Sci U S A. 2011 Apr 26;108(17):7265-70. doi: 10.1073/pnas.1102826108. Epub 2011 Apr 11. PMID: 21482760; PMCID: PMC3084136.
- Nowak MA. Five rules for the evolution of cooperation. Science. 2006 Dec 8;314(5805):1560-3. doi: 10.1126/science.1133755. PMID: 17158317; PMCID: PMC3279745.
- Fozard JA, Kirkham GR, Buttery LD, King JR, Jensen OE, Byrne HM. Techniques for analysing pattern formation in populations of stem cells and their progeny. BMC Bioinformatics. 2011 Oct 12;12:396. doi: 10.1186/1471-2105-12-396. PMID: 21991994; PMCID: PMC3252362.
- Nelson CM, Jean RP, Tan JL, Liu WF, Sniadecki NJ, Spector AA, Chen CS. Emergent patterns of growth controlled by multicellular form and mechanics. Proc Natl Acad Sci U S A. 2005 Aug 16;102(33):11594-9. doi: 10.1073/pnas.0502575102. Epub 2005 Jul 27. PMID: 16049098; PMCID: PMC1187971.
- Snyder JC, Rochelle LK, Marion S, Lyerly HK, Barak LS, Caron MG. Lgr4 and Lgr5 drive the formation of long actin-rich cytoneme-like membrane protrusions. J Cell Sci. 2015 Mar 15;128(6):1230-40. doi: 10.1242/jcs.166322. Epub 2015 Feb 4. PMID: 25653388; PMCID: PMC4359926.
- Imran Alsous J, Villoutreix P, Berezhkovskii AM, Shvartsman SY. Collective Growth in a Small Cell Network. Curr Biol. 2017 Sep 11;27(17):2670-2676.e4. doi: 10.1016/j.cub.2017.07.038. Epub 2017 Aug 31. PMID: 28867205; PMCID: PMC6333208.
- Mandal M, Ghosh B, Rajput M, Chatterjee J. Impact of intercellular connectivity on epithelial mesenchymal transition plasticity. Biochim Biophys Acta Mol Cell Res. 2020 Oct;1867(10):118784. doi: 10.1016/j.bbamcr.2020.118784. Epub 2020 Jun 23. PMID: 32590027.
- Waliszewski P. Computer-Aided Image Analysis and Fractal Synthesis in the Quantitative Evaluation of Tumor Aggressiveness in Prostate Carcinomas. Front Oncol. 2016 May 9;6:110. doi: 10.3389/fonc.2016.00110. PMID: 27242954; PMCID: PMC4860606.
Content Alerts
SignUp to our
Content alerts.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.