Mathematical Modelling of the Addiction of Drug Substances among Students in Tertiary Institutions in Nigeria

In this paper, we formulated a mathematical model for the addiction of drug substances among students in the tertiary institutions in Nigeria. The model explains the dynamics of the use and the addiction of certain substances that are perceived as mood changing by the students in the tertiary institutions in Nigeria. The drug model will be analysed qualitatively. The basic reproductive number which is the drug addiction number of the mathematical model was determined using the next generation procedure. It was found that the drug free equilibrium point was found to be locally asymptotically stable whenever the drug addiction number is less than one and unstable otherwise. The analysis revealed that an increase in the recruitment rate of students and the rate at which the students return to the use and addiction of drugs would cause an increase in the drug addiction number. There are impacts on interaction among non-drug users and drug users in the system with time. An increase in the contact or limitation rate increases the population of drug users. It is hereby recommended that; government should intensify efforts to reduce or stop the spread of selling and purchasing of the drug substances through government policies among the students in the tertiary institutions in Nigeria.

Drug abuse and addiction is a condition characterized by a self-destructive pattern of using a substance that leads to significant problems and distress which may include tolerance to or withdrawal from the substance. These drug abuse and addiction are both grouped as substance or drug use disorder. Drug use disorder is unfortunately quite common, affecting more than 8% of people in the country at some point in their lives [1]. People can abuse virtually any substance whose ingestion can result in a euphoric or high feeling while the specific physical and psychological effects of drug use disorder tend to vary based on the particular substance involved, the general effects of a substance use disorder involving any drug can be devastating.

In this paper, mathematical modelling of the addiction of drug substances among students in tertiary institutions in Nigeria is considered. Joan KavuteKanyaa, et al. [2] established and analyzed a deterministic mathematical model in their paper. However, the exposed class was not incorporated into their mathematical model. In this study, the exposed class was incorporated into this model and some other parameters were added in order to have a robust mathematical model on the addiction of drug substances among the students in the tertiary institutions. The stability analyses of both the drug free and the endemic equilibrium points were determined including the basic reproductive number of the new reformulated mathematical model. The basic reproductive number R0 is a threshold quantity that determines when a single drug abuse student invades a population. This number is obtained using the next generation approach as described by Diekmann and Hesterbeek [3,4].

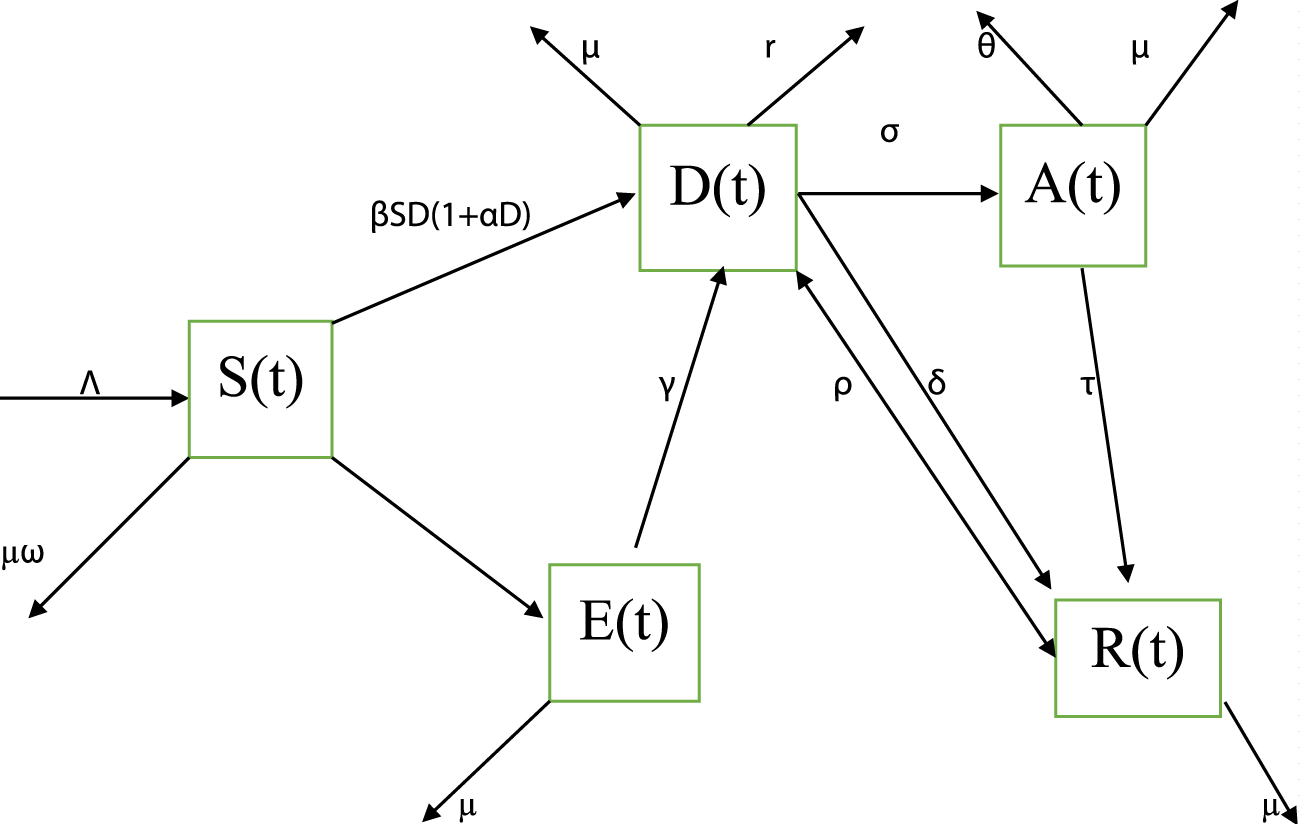
The mathematical model is divided into a system of ordinary differential equation with five different sets in compartmental form depending on their substances uses status. The five compartments include the susceptibles S(t) which comprises of all students that are at risk of using any substance (drug). All students who use any substance or drug of any form are grouped under drug users d(t). All students who are exposed to the use of the substance (drug) of any form are classified into the E(t) group. The compartment of all students who are addicted to the use of drugs are grouped under A(t) and those students who stopped using drugs either by abstinence or through rehabilitation or through parental guidance are under the class R(t). the rate at which the students are recruited into the susceptible class is Λ, the rate at which the students imitate their colleagues who use any substance is α and β is the rate at which students interact in the population while δ is the natural recovery rate of drug users and ρ is the rate at which students return to the use of drugs. The natural death rate of all the students is denoted by µ and σ is the rate at which all drug users are addicted to the use of substances (drugs). The parameters r and θ are the death rates of drug users and drug addicted respectively. The mathematical model is described by considering the dynamical equations for the student population. The mathematical model assumes that, those students who are recovered were still involved in the use of drug but not involved in the addiction of the drugs. The students are classified into five groups as susceptible, exposed, drug users, drug addicted and the recovered for the dynamical equations, the definitions of the variables and parameters used in the model are given in the table 1. In addition, the flow diagram of the drug users and the addicted among the students are shown in the figure 1.

Figure 1: Flow diagram of the model.

The total population of the students considered becomes:

$N\left(t\right)=S\left(t\right)+E\left(t\right)+D\left(t\right)+A\left(t\right)+R(t)\text{ (1)}$

The following system of equations are obtained from the model flow diagram in figure 1;

$\frac{dS}{dt}=\Lambda -\beta S\left(t\right)D\left(t\right)\left(1+\alpha D\right)-(\mu +\omega )S(t)\text{ (2)}$

$\frac{dE}{dt}=\omega S\left(t\right)-(\mu +\gamma )E(t)\text{ (3)}$

$\begin{array}{l}\frac{dD}{dt}=\gamma E\left(t\right)+\beta S\left(t\right)D\left(t\right)\left(1+\alpha D\left(t\right)\right)\\ -\left(\sigma +\delta +r+\mu \right)D\left(t\right)+\rho R(t)\text{ (4)}\end{array}$

$\frac{dA}{dt}=\sigma D\left(t\right)-(\theta +\tau +\mu )A(t)\text{ (5)}$

$\frac{dR}{dt}= \tau A\left(t\right)+\delta D\left(t\right)-(\mu +\rho )R(t)\text{ (6)}$

The solution of the system remains positive at any point in time if the initial values of all the variables are positive. From equation (1),

$\frac{dN}{dt}=\frac{dS}{dt}+\frac{dE}{dt}+\frac{dD}{dt}+\frac{dA}{dt}+\frac{dR}{dt}\text{ (7)}$

From equations (2) to (6), by simplification,

$\frac{dN}{dt}=\Lambda -\mu \left(S+E+R\right)-\left(r+\mu \right)D-(\theta +\mu )A\text{ (8)}$

Since there are no drug addicted, drug users, exposed and recovered students in the absence of drugs, hence, E = 0, D = 0, A = 0 and R = 0. Equation (8) becomes,

$\frac{dN}{dt}=\Lambda -\mu S(t)\text{ (9)}$

If the total population N is equal to the number of susceptible S, it implies that N = S, such that,

$\frac{dN}{dt}=\Lambda -\mu N\text{ (10)}$

On solving equation (10), we obtain,

$(\Lambda -\mu N)\ge e^{-\mu t}{e}^{-\mu B}\text{ (11)}$

where $P= e^{-\mu B}$ . Then, $\Lambda -\mu N\ge P{e}^{-\mu t}$ . Applying the conditions at $N\left(0\right)=S\left(0\right),\Lambda -\mu N\left(0\right)=P$ , therefore,

$\Lambda -\mu N=(\Lambda -\mu N(0))e^{-\mu t}\text{ (12)}$

Rearranging equation (12) and simplifying it becomes;

$N \le \frac{\Lambda }{\mu }-(\frac{(\Lambda -\mu N(0))}{\mu })e^{-\mu t}\text{ (13)}$

As t → ∞, the size of population $\text{N }\to \frac{\Lambda }{\mu }$ , this implies that; $0\le N(t)\le \frac{\Lambda }{\mu }$ and, $N(t)\le \frac{\Lambda }{\mu }$ therefore,

$\vartheta =\left\{\left(S,E,D,A, R\right) ϵ R_{+}^5:S+E+D+A+R\le \frac{\Lambda }{\mu }\right\}\text{ (14)}$

So, the dynamical change of each class equals to zero. Normalizing the dynamical equations (2) to (6) by setting, s = S/N, e = E/N, d = D/N, a = A/N and r = R/N, then, the reduced forms of the equations become:

$\frac{ds}{dt}=\Lambda -\beta s\left(t\right)d\left(t\right)\left(1+\alpha d(t)\right)-(\mu +\omega )s(t)\text{ (15)}$

$\frac{de}{dt}=\omega s\left(t\right)-(\mu +\gamma )e(t)\text{ (16)}$

$\begin{array}{l}\frac{dd}{dt}=\gamma e\left(t\right)+\beta s\left(t\right)d\left(t\right)\left(1+\alpha d\left(t\right)\right)-\\ \left(\sigma +\delta +r+\mu \right)d\left(t\right)+\rho r(t)\text{ (17)}\end{array}$

$\frac{da}{dt}=\sigma d\left(t\right)-(\theta +\tau +\mu )a(t)\text{ (18)}$

$\frac{dr}{dt}= \tau a\left(t\right)+\delta d\left(t\right)-(\mu +\rho )r(t)\text{ (19)}$

To find the equilibrium states of the mathematical model, the right-hand side of equations (15) to (19) are set equal to zero [5]. So, the equilibrium states are obtained as follows:

Drug free equilibrium state:

$H_0=\left(s^{*},e^{*},d^{*},a^{*},r^{*}\right)=(\frac{\Lambda }{\mu },0,0,0,0)\text{ (20)}$

The drug free equilibrium points are obtained when the system of differential equations are set to zero. At this point, there are no drug users, no addicted, no exposed and the recovered students. i.e. e* = 0, d* = 0, a* = 0 and r* = 0.

Drug endemic equilibrium state: where; $H_1=(s^{*},e^{*},d^{*},a^{*},r^{*})$

$s^{*}=\frac{\begin{array}{l}\left(\mu +\gamma \right)[\left(\theta +r+\mu \right)\left(\mu +\rho \right)\left(\sigma +\delta +r+\mu \right)-\\ (\tau \sigma +\delta (\theta +r+\mu ))]\end{array}}{\begin{array}{l}\omega \gamma \left(\theta +r+\mu \right)\left(\mu +\rho \right)+\beta \left(\theta +r+\mu \right)\left(\mu +\rho \right)\left(\mu +\gamma \right)+\\ \alpha \beta (\theta +r+\mu )(\mu +\rho )(\mu +\gamma )\end{array}}\text{ (21)}$

$e^{*}=\frac{\begin{array}{l}[\left(\theta +r+\mu \right)\left(\mu +\rho \right)\\ \left(\sigma +\delta +r+\mu \right)-(\tau \sigma +\delta (\theta +r+\mu ))]\end{array}}{\begin{array}{l}\gamma \left(\theta +r+\mu \right)\left(\mu +\rho \right)+\frac{\beta }{\omega }\left(\theta +r+\mu \right)\left(\mu +\rho \right)\\ \left(\mu +\gamma \right)+\frac{\alpha \beta }{\omega }(\theta +r+\mu )(\mu +\rho )(\mu +\gamma )\end{array}}\text{ (22)}$

$d^{*}=1\text{ (23)}$

$a^{*}=(\frac{\sigma }{\theta +r+\mu })\text{ (24)}$

$r^{*}=(\frac{\tau \sigma +\delta (\theta +r+\mu )}{(\theta +r+\mu )(\mu +\rho )})\text{ (25)}$

With these values for $s^{*},e^{*},d^{*},a^{*},r^{*}$ , the positivity and uniqueness of H₁ are guaranteed if and only if R₀ > 1 where R₀ is the basic reproductive number for the mathematical model given in the form

$R_0=\frac{\beta \Lambda }{\mu (\sigma +\delta +r+\mu )}\text{ (26)}$

In the drug endemic equilibrium state, the number of drug users is strictly positive and constant. So, if some of the solutions of the system of equations d(t) approach as time goes to infinity, the number of drug users will remain strictly positive for a long time and approximately equal to d(t). Thus, the use of drugs will remain in the population and becomes endemic except adequate measures are put in place to control and prevent the rapid spread of the use of drugs among the students in the tertiary institutions.

There are early signs risk that may dictate and predict later drug abuse from adolescent to adult. Some signs of risk can be seen as early as infancy. Children’s personality traits and temperaments can place them at increased risk for later drug abuse. Withdrawn and aggressive boys, for example, often exhibit problem behaviors in interactions with their families, peers, and others they encounter in social settings. If these behaviors continue, they will likely lead to other risks. These risks can include academic failure, early peer rejection, and later affiliation with deviant peers, often the most immediate risk for drug abuse in adolescence. Studies have shown that children with poor academic performance and inappropriate social behavior at ages 7 to 9 are more likely to be involved with substance abuse by age 14 or 15.

Based on the content of the write up, it is imperative to examine the progress of drug abuse among students in tertiary institutions. Some children even before university education are already abusing drugs by age 12 or 13, which likely means that some may begin even earlier. Early abuse includes such drugs as tobacco, alcohol, inhalants, marijuana, and psychotherapeutic drugs. If drug abuse persists into later adolescence, abusers typically become more involved with marijuana and then advance to other illegal drugs, while continuing their abuse of tobacco and alcohol. Studies have also shown that early initiation of drug abuse is associated with greater drug involvement, whether with the same or different drugs.

In general, the pattern of abuse is associated with levels of social disapproval, perceived risk, and the availability of drugs in the community/tertiary institution. Scientists have proposed several hypotheses as to why individuals first become involved with drugs and then escalate to abuse. One explanation is a biological cause, such as having a family history of drug or alcohol abuse, which may genetically predispose a person to drug abuse. Another explanation is that, starting to abuse a drug may lead to affiliation with more drug-abusing peers which, in turn, exposes the individual to other drugs. Indeed, many factors may be involved.

Different patterns of drug initiation have been identified based on gender, race or ethnicity, and geographic location. For example, research has found that the circumstances in which young people are offered drugs can depend on gender. Boys generally receive more drug offers and at younger ages. Initial drug abuse can also be influenced by where drugs are offered, such as parks, streets, schools, homes, or parties.

Researchers have found that these youths are the most likely to have experienced a combination of high levels of risk factors with low levels of protective factors. These adolescents were characterized by high stress, low parental support, and low academic competence. However, there are protective factors that can suppress the escalation to substance abuse. These factors include self-control, which tends to inhibit problem behavior and often increases naturally as children mature during adolescence. In addition, protective family structure, individual personality, and environmental variables can reduce the impact of serious risks of drug abuse. Preventive interventions can provide skills and support to high-risk youth to enhance levels of protective factors and prevent escalation to drug abuse.

At this stage, the risk factors and protective factors for drug abuse among student in tertiary institution of learning should be mention for the clarity of purpose. Student don’t start the abuse in the university, it is a progressive stage from community to primary school to secondary and to tertiary institutions. This prevention may enhance protective factors and thereby reverse the predominant risk factors [6].

The protection and prevention factors are as follows in a logical sequence:

• The risk of becoming a drug abuser involves the relationship among the number and type of risk factors (e.g., deviant attitudes and behaviors) and protective factors (e.g., parental support) [7].
• The potential impact of specific risk and protective factors changes with age. For example, risk factors within the family have greater impact on a younger child, while association with drug-abusing peers may be a more significant risk factor for an adolescent [8,9].
• Early intervention with risk factors (e.g., aggressive behavior and poor self-control) often has a greater impact than later intervention by changing a child’s life path (trajectory) away from problems and toward positive behaviors [10].
• While risk and protective factors can affect people of all groups, these factors can have a different effect depending on a person’s age, gender, ethnicity, culture, and environment [11,12].

Prevention programs should address all forms of drug addict:

• Alone or in combination, including the underage use of legal drugs (e.g., tobacco or alcohol); the use of illegal drugs (e.g., marijuana or heroin); and the inappropriate use of legally obtained substances (e.g., inhalants), prescription medications, or over-the-counter drugs [13].
• Prevention programs should address the type of drug abuse problems in the local community, target modifiable risk factors, and strengthen identified protective factors [14].
• Prevention programs should be tailored to address risks specific to population or audience characteristics, such as age, gender, and ethnicity, to improve program effectiveness [15].
• Family bonding is the bedrock of the relationship between parents and children. Bonding can be strengthened through skills training on parent supportiveness of children, parent-child communication, and parental involvement [16,17].
• Parental monitoring and supervision are critical for drug abuse prevention. These skills can be enhanced with training on rule-setting; techniques for monitoring activities; praise for appropriate behavior; and moderate, consistent discipline that enforces defined family rules [18].
• Drug education and information for parents or caregivers reinforces what children are learning about the harmful effects of drugs and opens opportunities for family discussions about the abuse of legal and illegal substances [19].
• Family-focused interventions for the general population can positively change specific parenting behavior that can reduce later risks of drug abuse [20].

The administrators in tertiary institutions for the matter of urgency may include the following core values in the institution curriculum especially in civil education, to reduce the risk factors to drug abuse

• Self-control
• Emotional awareness
• Communication
• Social problem-solving
• Academic support, especially in reading.

Prevention programs for middle or junior high and high school students should increase academic and social competence with the following skills [21,22];

• Study habits and academic support
• Communication; peer relationships
• Self-efficacy and assertiveness
• Drug resistance skills
• Reinforcement of antidrug attitudes
• Strengthening of personal commitments against drug abuse

The drug mathematical model was qualitatively analyzed to give an account of drug spread among the students of tertiary institutions in Nigeria. The basic reproductive number of the mathematical model was computed. The use and the addiction of substances would continue to rise among the students if the basic reproductive number is less than one and the addiction of drugs would die out of the system if the reproductive number is greater than one. Recommendations were made to the government and the administrators of the institutions on how to reduce the rise in the addiction of drugs among the students of tertiary institutions.

1. Edgardo Perez Reyes. Mathematical modelling of the spread of alcoholism among Colombian college students. ing Cienc. 2020;16:195-223. doi: 10.17230/ingciencia.16.32.9
2. Kanyaa JK, Osman S, Wainaina M. Mathematical modelling of substance abuse by commercial drivers. Global Journal of Pure and Applied Mathematics. 2018;14:1149-1165. https://tinyurl.com/ruzhzptr
3. Diekmann O, Heesterbeek JA, Roberts MG. The construction of next-generation matrices for compartmental epidemic models. J R Soc Interface. 2010 Jun 6;7(47):873-85. doi: 10.1098/rsif.2009.0386. Epub 2009 Nov 5. PMID: 19892718; PMCID: PMC2871801.
4. Cushing JM, Diekmann O. The many guises of R0 (a didactic note). J Theor Biol. 2016 Sep 7;404:295-302. doi: 10.1016/j.jtbi.2016.06.017. Epub 2016 Jun 16. PMID: 27320680.
5. Adeyemi OB. A deterministic model for the transmission dynamics of infectious diseases among infants. Elixir Applied Mathematics. 2015;78:29761-29764. https://tinyurl.com/b55pecv3
6. Hawkins JD, Catalano RF, Arthur MW. Promoting science-based prevention in communities. Addict Behav. 2002 Nov-Dec;27(6):951-76. doi: 10.1016/s0306-4603(02)00298-8. PMID: 12369478.
7. Wills TA, Vaccaro D, McNamara G, Hirky AE. Escalated substance use: a longitudinal grouping analysis from early to middle adolescence. J Abnorm Psychol. 1996 May;105(2):166-80. doi: 10.1037//0021-843x.105.2.166. PMID: 8722998.
8. National Research Council (US) Committee on Substance Abuse Prevention Research. Preventing Drug Abuse: What do we know? Gerstein DR, Green LW, editors. Washington (DC): National Academies Press (US); 1993. PMID: 25121319.
9. Kumpfer KL.; Olds DL, Alexander JF, Zucker RA, Gary LE. Family etiology of youth problems. In: Ashery RS, Robertson EB, Kumpfer KL, editors. Drug abuse prevention through family interventions. NIDA Research Monograph No. 177. Washington, DC: US Government Printing Office. 1998;42-77.
10. Ialongo NS, Werthamer L, Kellam SG, Brown CH, Wang S, Lin Y. Proximal impact of two first-grade preventive interventions on the early risk behaviors for later substance abuse, depression, and antisocial behavior. Am J Community Psychol. 1999 Oct;27(5):599-641. doi: 10.1023/A:1022137920532. PMID: 10676542.
11. Oetting E, Edwards R, Kelly K, Beauvais F. Risk and protective factors for drug use among rural American youth. In: Robertson EB, Sloboda Z, Boyd GM, Beatty L, Kozel NJ, editors. Rural Substance Abuse: State of Knowledge and Issues. NIDA Research Monograph No. 168. Washington, DC: US Government Printing Office. 1997;90-130.
12. Moon DG, Hecht ML, Jackson KM, Spellers RE. Ethnic and gender differences and similarities in adolescent drug use and refusals of drug offers. Subst Use Misuse. 1999 Jun;34(8):1059-83. doi: 10.3109/10826089909039397. PMID: 10359222.
13. Johnston LD, O’Malley PM, Bachman JG. Monitoring the future national survey results on drug use. 1975–2002. Volume 1: Secondary School Students. Bethesda, MD: National Institute on Drug Abuse, 2002. https://tinyurl.com/c62exujw
14. Hawkins JD, Catalano RF, Arthur MW. Promoting science-based prevention in communities. Addict Behav. 2002 Nov-Dec;27(6):951-76. doi: 10.1016/s0306-4603(02)00298-8. PMID: 12369478.
15. Oetting E, Edwards R, Kelly K, Beauvais F. Risk and protective factors for drug use among rural American youth. In: Robertson EB, Sloboda Z, Boyd GM, Beatty L, Kozel NJ, editors. Rural Substance Abuse: State of Knowledge and Issues. NIDA Research Monograph No. 168. Washington, DC: US Government Printing Office; 1997;90-130.
16. Kosterman R, Hawkins JD, Spoth R, Haggerty KP, Zhu K. Effects of a preventive parent-training intervention on observed family interactions: Proximal outcomes from preparing for the drug free years. Journal of Community Psychology. 1997;25(4):337-352.
17. Ashery RS, Robertson EB, Kumpfer KL, editors. Drug abuse prevention through family interventions. NIDA research monograph No. 177. Washington, DC: U.S Government Printing Office. 1998.
18. Kosterman R, Hawkins JD, Haggerty KP, Spoth R, Redmond C. Preparing for the drug free years: session-specific effects of a universal parent-training intervention with rural families. J Drug Educ. 2001;31(1):47-68. doi: 10.2190/3KP9-V42V-V38L-6G0Y. PMID: 11338965.
19. Bauman KE, Foshee VA, Ennett ST, Pemberton M, Hicks KA, King TS, Koch GG. The influence of a family program on adolescent tobacco and alcohol use. Am J Public Health. 2001 Apr;91(4):604-10. doi: 10.2105/ajph.91.4.604. PMID: 11291373; PMCID: PMC1446646.
20. Spoth RL, Redmond C, Trudeau L, Shin C. Longitudinal substance initiation outcomes for a universal preventive intervention combining family and school programs. Psychol Addict Behav. 2002 Jun;16(2):129-34. PMID: 12079251.
21. Botvin GJ, Baker E, Dusenbury L, Botvin EM, Diaz T. Long-term follow-up results of a randomized drug abuse prevention trial in a white middle-class population. JAMA. 1995 Apr 12;273(14):1106-12. PMID: 7707598.
22. Scheier LM, Botvin GJ, Diaz T, Griffin KW. Social skills, competence, and drug refusal efficacy as predictors of adolescent alcohol use. J Drug Educ. 1999;29(3):251-78. doi: 10.2190/M3CT-WWJM-5JAQ-WP15. PMID: 10645126.